沪科版七年级下册9.3.4分式方程的应用2(行程问题) 课件(共11张PPT)
文档属性
| 名称 | 沪科版七年级下册9.3.4分式方程的应用2(行程问题) 课件(共11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 665.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 00:00:00 | ||
图片预览




文档简介
(共11张PPT)
分式方程的应用 (行程问题)
学习目标
1.会用分式方程解决行程问题。
2.掌握分式方程解应用题的一般步骤。
独立自学
为了满足经济高速发展的需求 ,我国铁路部门不断进行技术革新,提高列车的运行速度。
在相距1600km的两地之间运行一列车,速度提高25%后,运行时间缩短了4h,你能求出列车提速前的速度吗?
问题一:题目中的哪些量是已知的,哪些量是未知的,你能找到其中的等量关系么?
问题二:若设提速前速度为x km/h ,完成下面的表格
路程km 速度km/h 时间h
提速前
提速后
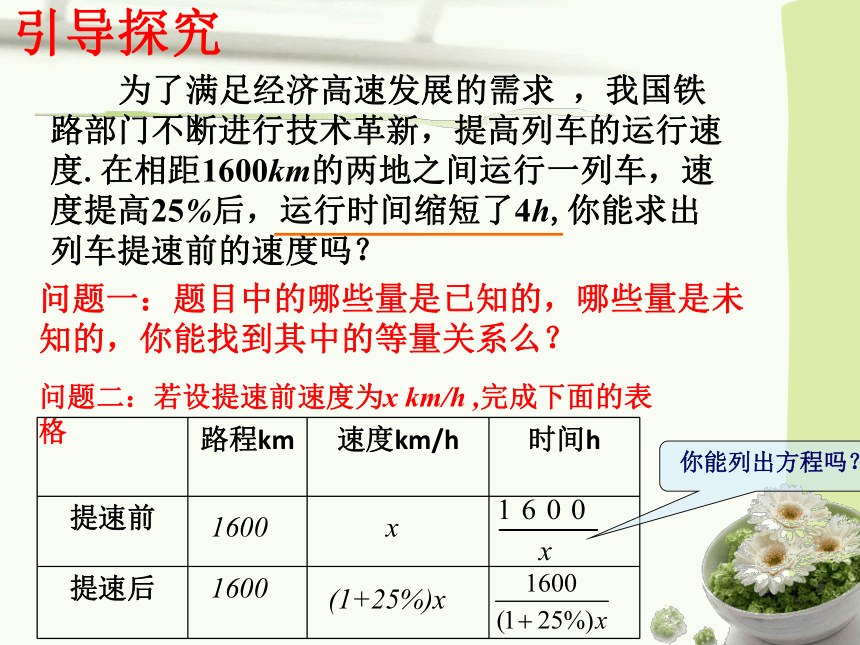
引导探究
为了满足经济高速发展的需求 ,我国铁路部门不断进行技术革新,提高列车的运行速度.在相距1600km的两地之间运行一列车,速度提高25%后,运行时间缩短了4h,你能求出列车提速前的速度吗?
问题一:题目中的哪些量是已知的,哪些量是未知的,你能找到其中的等量关系么?
问题二:若设提速前速度为x km/h ,完成下面的表格
1600
1600
x
(1+25%)x
你能列出方程吗?
路程km 速度km/h 时间h
提速前
提速后
引导探究
解:设提速前的速度为x km/h,根据题意,得:
解得:
经检验,x=80是该分式方程的解
答:列车提速前的速度是80km/h
甲、乙二人都要走15千米的路,甲的速度是乙的速度的1.2倍,甲比乙少用0.5小时,甲乙二人的速度各是多少?
学以致用
思路分析:假设乙的速度为x千米/时,则甲的速度为1.2x千米/时
1.2x
x
15
15
请找出等量关系列方程!!
乙的时间-甲的时间=0.5小时
速度
(千米/时) 路程(千米) 时间(时)
甲
乙
学以致用
某农机厂到距离工厂15千米的某地检修农机,一部分人骑自行车先走过了40分钟,其余人乘汽车出发,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度。
设自行车的速度是X千米/时,汽车的速度是3X千米/时
思路分析:
x
3x
15
15
请找出可列方程的等量关系
骑自行车的时间-乘汽车的时间= 小时
速度(千米/时) 路程(千米) 时间(时)
自行车
汽车
航行问题
1、航行问题中涉及的量有哪些?
顺水速度,逆水速度,水流速度
2、它们之间的关系式什么?
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
一艘轮船顺水航行66千米所用的时间与逆水航行48千米所用的时间相同,若水流速度为3千米/时,求轮船在静水中的速度。
思路分析
假设轮船在静水中的速度为x千米/时
x+3
66
x-3
48
学以致用
请找出等量关系列方程!!
顺水航行时间=逆水航行时间
速度
(千米/时) 路程(千米) 时间(时)
顺水
逆水
甲、乙两港路程为60千米,一船顺流由甲驶向乙,驶了一段时间,后因故折返甲,逆流行驶了10千米,然后掉头驶往乙港,这样花的时间与该船直接从乙港驶向甲港的时间相同。如果水流速度为2千米/时,求船在静水中的速度。
思路分析:若设船静水中的速度为X千米/时,则顺流的速 度为(X+2)千米/时,逆流的速度为(X-2)千米/时
甲
乙
10千米
顺流
逆流返回
在这个过程中顺流航行了多少千米?逆流航行了多少千米?
70千米
10千米
拓展提升
当堂小结
谈谈你对这节课的收获.
分式方程的应用 (行程问题)
学习目标
1.会用分式方程解决行程问题。
2.掌握分式方程解应用题的一般步骤。
独立自学
为了满足经济高速发展的需求 ,我国铁路部门不断进行技术革新,提高列车的运行速度。
在相距1600km的两地之间运行一列车,速度提高25%后,运行时间缩短了4h,你能求出列车提速前的速度吗?
问题一:题目中的哪些量是已知的,哪些量是未知的,你能找到其中的等量关系么?
问题二:若设提速前速度为x km/h ,完成下面的表格
路程km 速度km/h 时间h
提速前
提速后
引导探究
为了满足经济高速发展的需求 ,我国铁路部门不断进行技术革新,提高列车的运行速度.在相距1600km的两地之间运行一列车,速度提高25%后,运行时间缩短了4h,你能求出列车提速前的速度吗?
问题一:题目中的哪些量是已知的,哪些量是未知的,你能找到其中的等量关系么?
问题二:若设提速前速度为x km/h ,完成下面的表格
1600
1600
x
(1+25%)x
你能列出方程吗?
路程km 速度km/h 时间h
提速前
提速后
引导探究
解:设提速前的速度为x km/h,根据题意,得:
解得:
经检验,x=80是该分式方程的解
答:列车提速前的速度是80km/h
甲、乙二人都要走15千米的路,甲的速度是乙的速度的1.2倍,甲比乙少用0.5小时,甲乙二人的速度各是多少?
学以致用
思路分析:假设乙的速度为x千米/时,则甲的速度为1.2x千米/时
1.2x
x
15
15
请找出等量关系列方程!!
乙的时间-甲的时间=0.5小时
速度
(千米/时) 路程(千米) 时间(时)
甲
乙
学以致用
某农机厂到距离工厂15千米的某地检修农机,一部分人骑自行车先走过了40分钟,其余人乘汽车出发,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度。
设自行车的速度是X千米/时,汽车的速度是3X千米/时
思路分析:
x
3x
15
15
请找出可列方程的等量关系
骑自行车的时间-乘汽车的时间= 小时
速度(千米/时) 路程(千米) 时间(时)
自行车
汽车
航行问题
1、航行问题中涉及的量有哪些?
顺水速度,逆水速度,水流速度
2、它们之间的关系式什么?
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
一艘轮船顺水航行66千米所用的时间与逆水航行48千米所用的时间相同,若水流速度为3千米/时,求轮船在静水中的速度。
思路分析
假设轮船在静水中的速度为x千米/时
x+3
66
x-3
48
学以致用
请找出等量关系列方程!!
顺水航行时间=逆水航行时间
速度
(千米/时) 路程(千米) 时间(时)
顺水
逆水
甲、乙两港路程为60千米,一船顺流由甲驶向乙,驶了一段时间,后因故折返甲,逆流行驶了10千米,然后掉头驶往乙港,这样花的时间与该船直接从乙港驶向甲港的时间相同。如果水流速度为2千米/时,求船在静水中的速度。
思路分析:若设船静水中的速度为X千米/时,则顺流的速 度为(X+2)千米/时,逆流的速度为(X-2)千米/时
甲
乙
10千米
顺流
逆流返回
在这个过程中顺流航行了多少千米?逆流航行了多少千米?
70千米
10千米
拓展提升
当堂小结
谈谈你对这节课的收获.
