沪科版七年级下册9.3.2分式方程的应用——工程问题(共12张PPT)
文档属性
| 名称 | 沪科版七年级下册9.3.2分式方程的应用——工程问题(共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 566.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 11:57:06 | ||
图片预览




文档简介
(共12张PPT)
9.3.2分式方程的应用
工程问题
学习目标
1、能利用分式方程解决工程问题;
2、掌握列分式方程解决实际问题的
一般步骤.
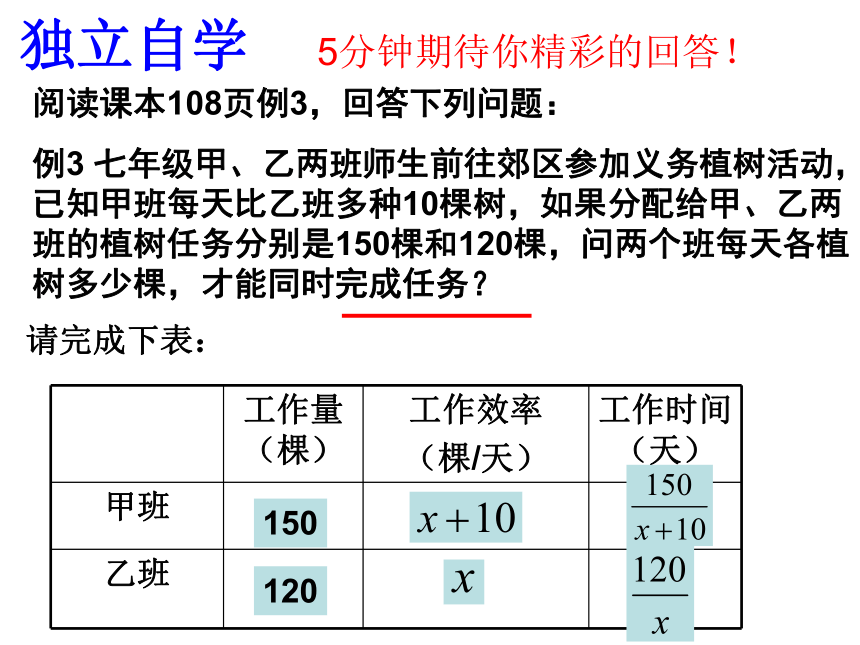
阅读课本108页例3,回答下列问题:
例3 七年级甲、乙两班师生前往郊区参加义务植树活动,已知甲班每天比乙班多种10棵树,如果分配给甲、乙两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
请完成下表:
独立自学
5分钟期待你精彩的回答!
150
120
工作量(棵) 工作效率
(棵/天) 工作时间(天)
甲班
乙班
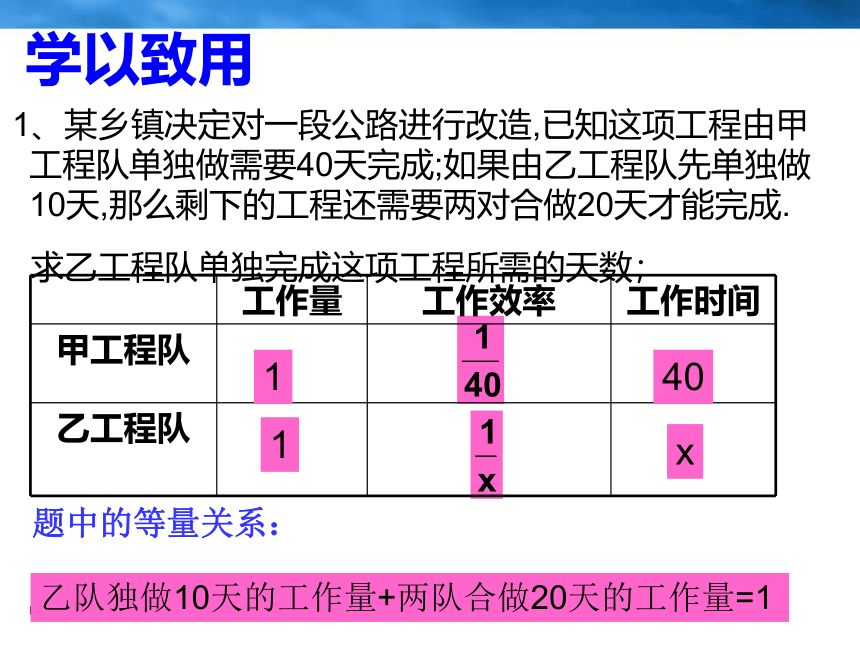
学以致用
1、某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程队先单独做10天,那么剩下的工程还需要两对合做20天才能完成.
求乙工程队单独完成这项工程所需的天数;
题中的等量关系:
1
x
乙队独做10天的工作量+两队合做20天的工作量=1
1
40
工作量 工作效率 工作时间
甲工程队
乙工程队
解:设乙工程队单独完成需要x天,根据题意得:
解得 x=60
经检验:x=60是原方程的根。
所以乙工程队单独完成需要60天.
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据等量关系,列出分式方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.
两次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
归纳小结
2、甲、乙两个学生分别向计算机输入1500个汉字,乙的速度是甲的3倍,因此比甲少用20分钟完成任务,他们平均每分钟输入汉字多少个?
分析:应用题中的数量关系
等量关系:甲用时间=乙用时间+20(分钟)
1500个
1500个
x个/分
3x个/分
学以致用
工作量 工作效率 工作时间
甲
乙
学以致用
3、甲、乙两名工人生产同一种零件,甲每时比乙多生产8个,甲生产168个零件与乙生产144个零件所用的时间相同,问甲、乙两人每时各生产多少个零件?
例4、某农场原计划在若干天内收割小麦960公顷,但实际工作效率比原计划提高了50%,结果提前4天完成任务,试求原计划每天收割多少公顷及原计划的天数。
分析:设原计划每天收割x公顷。应用题中的数量关系为:
等量关系:原计划天数=实际天数+4(天)
960公顷
960公顷
x公顷/天
(1+50%)x公顷/天
例题讲解
工作量 工作效率 工作时间
原计划情况
实际情况
学以致用
4、马鞍山市政府打算把一块荒地建成公园,动用了一台甲型挖土机,4天挖完了这块地的一半。后又加一台乙型挖土机,两台挖土机一起挖,结果1天就挖完了这块地的另一半。乙型挖土机单独挖这块地需要几天?
分析:请完成下列填空:
(1)设乙型挖土机单独挖这块地需要x天,它的工作效率是_______;
(2)甲型挖土机需要 天可挖完,它的工作效率是______;
(3)两台挖土机合挖,1天挖土量是这块地的_____.
8
解:设乙型挖土机单独挖这块地需要x天,根据题意得:
解方程,得 x=
因为x为正整数,所以x=3
经检验:x=3是原方程的根。
答:乙型挖土机单独挖这块地需要3天.
课堂小结
谈谈你的收获!
9.3.2分式方程的应用
工程问题
学习目标
1、能利用分式方程解决工程问题;
2、掌握列分式方程解决实际问题的
一般步骤.
阅读课本108页例3,回答下列问题:
例3 七年级甲、乙两班师生前往郊区参加义务植树活动,已知甲班每天比乙班多种10棵树,如果分配给甲、乙两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
请完成下表:
独立自学
5分钟期待你精彩的回答!
150
120
工作量(棵) 工作效率
(棵/天) 工作时间(天)
甲班
乙班
学以致用
1、某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程队先单独做10天,那么剩下的工程还需要两对合做20天才能完成.
求乙工程队单独完成这项工程所需的天数;
题中的等量关系:
1
x
乙队独做10天的工作量+两队合做20天的工作量=1
1
40
工作量 工作效率 工作时间
甲工程队
乙工程队
解:设乙工程队单独完成需要x天,根据题意得:
解得 x=60
经检验:x=60是原方程的根。
所以乙工程队单独完成需要60天.
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据等量关系,列出分式方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.
两次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
归纳小结
2、甲、乙两个学生分别向计算机输入1500个汉字,乙的速度是甲的3倍,因此比甲少用20分钟完成任务,他们平均每分钟输入汉字多少个?
分析:应用题中的数量关系
等量关系:甲用时间=乙用时间+20(分钟)
1500个
1500个
x个/分
3x个/分
学以致用
工作量 工作效率 工作时间
甲
乙
学以致用
3、甲、乙两名工人生产同一种零件,甲每时比乙多生产8个,甲生产168个零件与乙生产144个零件所用的时间相同,问甲、乙两人每时各生产多少个零件?
例4、某农场原计划在若干天内收割小麦960公顷,但实际工作效率比原计划提高了50%,结果提前4天完成任务,试求原计划每天收割多少公顷及原计划的天数。
分析:设原计划每天收割x公顷。应用题中的数量关系为:
等量关系:原计划天数=实际天数+4(天)
960公顷
960公顷
x公顷/天
(1+50%)x公顷/天
例题讲解
工作量 工作效率 工作时间
原计划情况
实际情况
学以致用
4、马鞍山市政府打算把一块荒地建成公园,动用了一台甲型挖土机,4天挖完了这块地的一半。后又加一台乙型挖土机,两台挖土机一起挖,结果1天就挖完了这块地的另一半。乙型挖土机单独挖这块地需要几天?
分析:请完成下列填空:
(1)设乙型挖土机单独挖这块地需要x天,它的工作效率是_______;
(2)甲型挖土机需要 天可挖完,它的工作效率是______;
(3)两台挖土机合挖,1天挖土量是这块地的_____.
8
解:设乙型挖土机单独挖这块地需要x天,根据题意得:
解方程,得 x=
因为x为正整数,所以x=3
经检验:x=3是原方程的根。
答:乙型挖土机单独挖这块地需要3天.
课堂小结
谈谈你的收获!
