苏科版八年级下9.4矩形、菱形、正方形 45分钟限时提优训练含答案
文档属性
| 名称 | 苏科版八年级下9.4矩形、菱形、正方形 45分钟限时提优训练含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 330.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-11 10:54:02 | ||
图片预览



文档简介
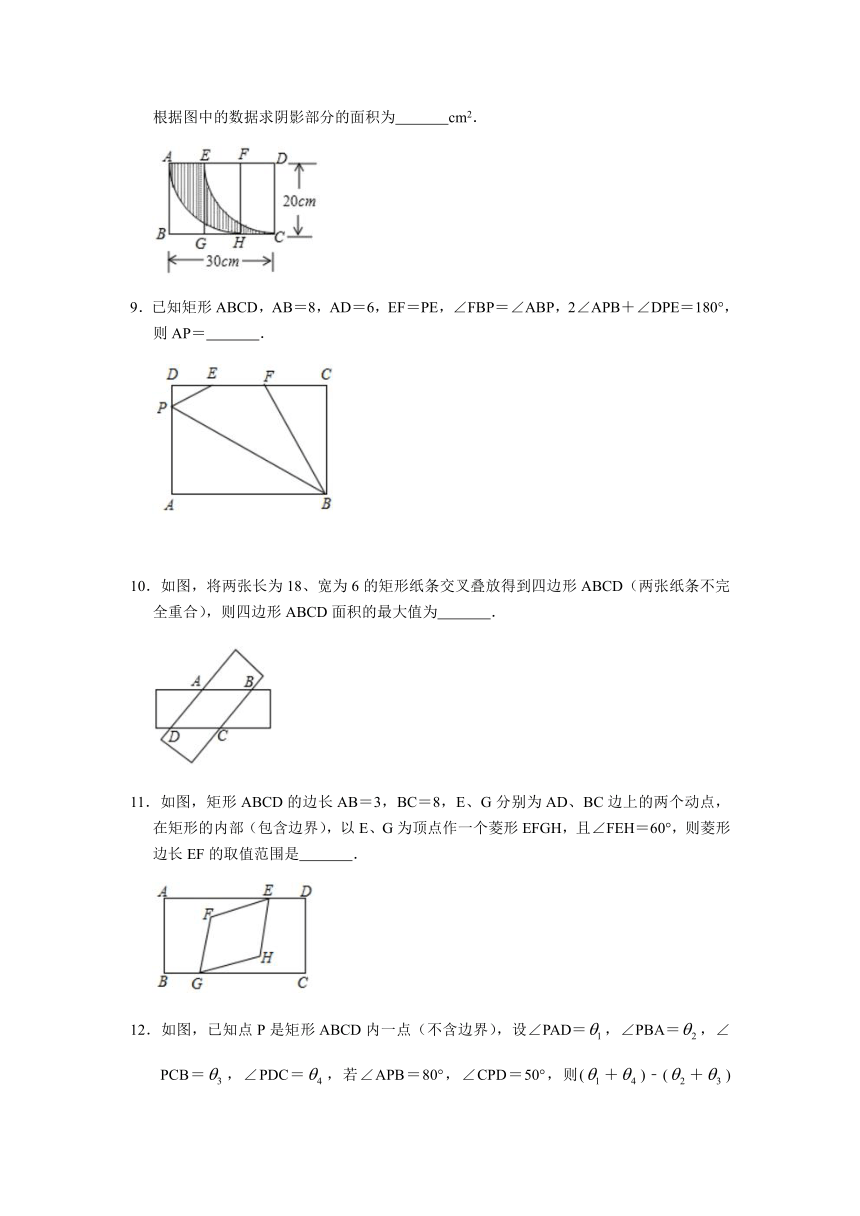
苏科版八年级下学期9.4矩形、菱形、正方形 60分钟限时提优训练
测试内容:矩形的性质与判定
1.如图,点P是矩形ABCD内一点(不含边界),若S△PAB=S△PBC,则点P一定在
A.在对角线BD上 B.在对角线AC上
C.在对角线AC和BD的交点处 D.在∠ABC的平分线上
2.如图,矩形ABCD中,AB=8,BC=4.点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是
A. B.5 C. D.6
3.如图,在矩形ABMN中,AN=1,点C是MN的中点,分别连接AC,BC,且BC=2,点D为AC的中点,点E为边AB上一个动点,连接DE,点A关于直线DE的对称点为点F,分别连接DF,EF.当EF⊥AC时,AE的长为 .
4.在探究“尺规三等分角”这个数学名题中,利用了如图,该图中,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是 .
5.如图,长方形ABCD中,AB=4,AD=3,长方形内有一个点P,连结AP,BP,CP,已知∠APB=90°,CP=CB,延长CP交AD于点E,则AE= .
6.如图,在平面直角坐标系中,矩形OABC的边OA=6,OC=2,一条动直线l分别与BC、OA交于点E、F,且将矩形OABC分为面积相等的两部分,则点O到动直线l的距离的最大值为 .
7.在矩形ABCD中,已知AD=4,AB=3,P是AD上任意一点,PE⊥BD于E,PF⊥AC于F,则PE+PF的值为 .
8.如图,四边形ABCD是一个矩形,E、F、G、H分别是边AD、BC上的三等分点,请你根据图中的数据求阴影部分的面积为 cm2.
9.已知矩形ABCD,AB=8,AD=6,EF=PE,∠FBP=∠ABP,2∠APB+∠DPE=180°,则AP= .
10.如图,将两张长为18、宽为6的矩形纸条交叉叠放得到四边形ABCD(两张纸条不完全重合),则四边形ABCD面积的最大值为 .
11.如图,矩形ABCD的边长AB=3,BC=8,E、G分别为AD、BC边上的两个动点,在矩形的内部(包含边界),以E、G为顶点作一个菱形EFGH,且∠FEH=60°,则菱形边长EF的取值范围是 .
12.如图,已知点P是矩形ABCD内一点(不含边界),设∠PAD=,∠PBA=,∠PCB=,∠PDC=,若∠APB=80°,∠CPD=50°,则(+)﹣(+)= .
13.如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,若FD=FG,BF=,BG=4,则点B到FG的距离为 .
14.如图,在平行四边形ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF.
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4.求CG.
15.如图,AC、BD相交于点O,且O是AC、BD的中点,点E在四边形ABCD外,且∠AEC=∠BED=90°,求证:四边形ABCD是矩形.
16.如图,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线交折线OAB于点E.
(1)记△ODE的面积为S,求S与b的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.
参考答案
1.A 2.B 3.或 4.23° 5. 6. 7.
8.200 9. 10.60 11.≤EF≤ 12.30° 13.
14.
15.
16.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
