人教版七年级数学下册第九章《一元一次不等式与不等式组的解法》复习教案
文档属性
| 名称 | 人教版七年级数学下册第九章《一元一次不等式与不等式组的解法》复习教案 | 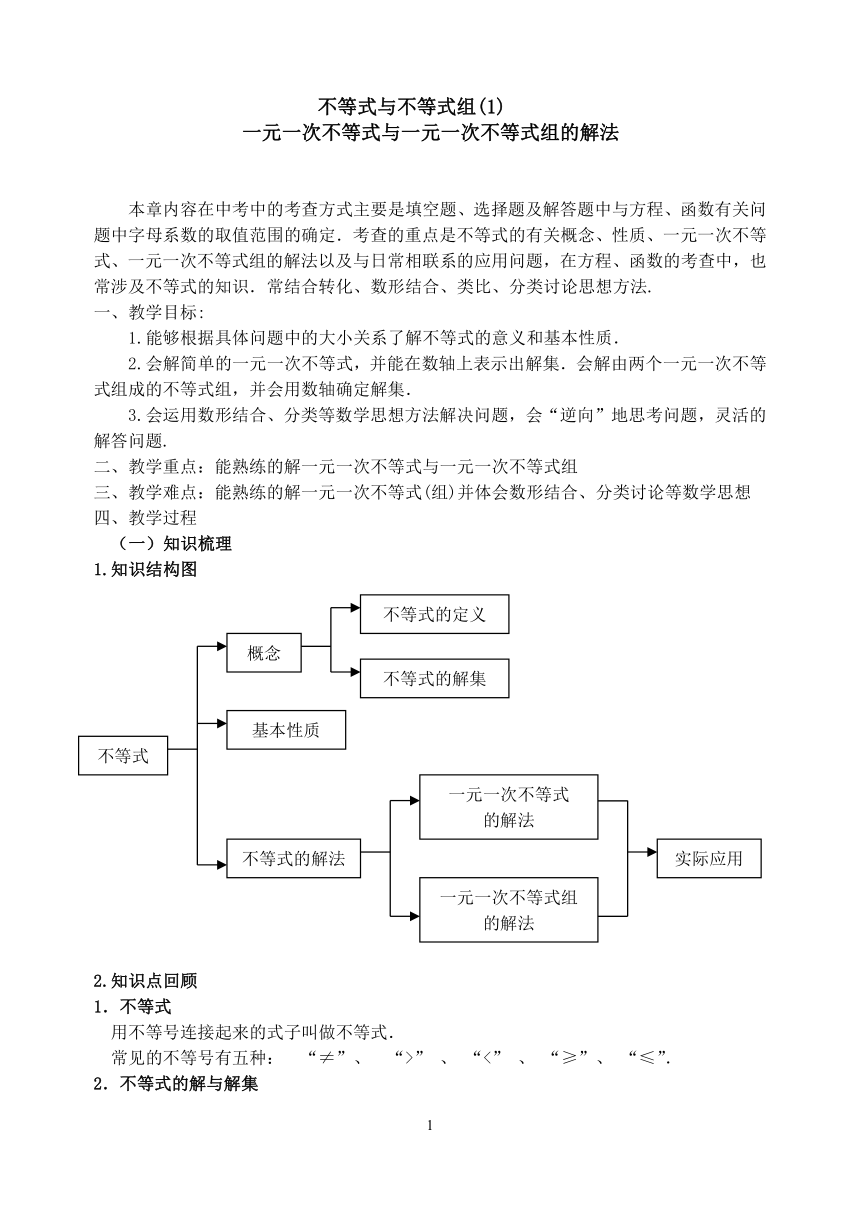 | |
| 格式 | zip | ||
| 文件大小 | 329.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-10 16:36:33 | ||
图片预览


文档简介
不等式与不等式组(1)
一元一次不等式与一元一次不等式组的解法
本章内容在中考中的考查方式主要是填空题、选择题及解答题中与方程、函数有关问题中字母系数的取值范围的确定.考查的重点是不等式的有关概念、性质、一元一次不等式、一元一次不等式组的解法以及与日常相联系的应用问题,在方程、函数的考查中,也常涉及不等式的知识.常结合转化、数形结合、类比、分类讨论思想方法.
一、教学目标:
1.能够根据具体问题中的大小关系了解不等式的意义和基本性质.
2.会解简单的一元一次不等式,并能在数轴上表示出解集.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集.
3.会运用数形结合、分类等数学思想方法解决问题,会“逆向”地思考问题,灵活的解答问题.
二、教学重点:能熟练的解一元一次不等式与一元一次不等式组
三、教学难点:能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想
四、教学过程
(一)知识梳理
1.知识结构图
2.知识点回顾
1.不等式
用不等号连接起来的式子叫做不等式.
常见的不等号有五种: “≠”、 “>” 、 “<” 、 “≥”、 “≤”.
2.不等式的解与解集
不等式的解:使不等式成立的未知数的值,叫做不等式的解.
不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.
不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.
3.不等式的基本性质
(1)不等式的两边都加上(或减去)同一个数或同一个整式.不等号的方向不变.如果,那么
(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.如果,那么(或)
(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.如果那么(或)
说明:任意两个实数a、b的大小关系:①a-b>Oa>b;②a-b=Oa=b;③a-b4.一元一次不等式
只含有一个未知数,且未知数的次数是1.系数不等于0的不等式叫做一元一次不等式.
注:一元一次不等式的一般形式是ax+b>O或ax+b5.解一元一次不等式的一般步骤
解一元一次不等式的一般步骤:
(1)去分母;(2)去括号;(3)移项; (4)合并同类项;(5)化系数为1.
说明:解一元一次不等式和解一元一次方程类似.不同的是:一元一次不等式两边同乘以(或除以)同一个负数时,不等号的方向必须改变,这是解不等式时最容易出错的地方.
6.一元一次不等式组
含有相同未知数的几个一元一次不等式所组成的不等式组,叫做一元一次不等式组.
说明:判断一个不等式组是一元一次不等式组需满足两个条件:①组成不等式组的每一个不等式必须是一元一次不等式,且未知数相同;②不等式组中不等式的个数至少是2个,也就是说,可以是2个、3个、4个或更多.
7.一元一次不等式组的解集
一元一次不等式组中,几个不等式解集的公共部分.叫做这个一元一次不等式组的解集.
一元一次不等式组的解集通常利用数轴来确定.
8. 不等式组解集的确定方法,可以归纳为以下四种类型(设a>b)
不等式组 图示 解集
(同大取大)
(同小取小)
(大小交叉取中间)
无解(大小分离解为空)
9.解一元一次不等式组的步骤
(1)分别求出不等式组中各个不等式的解集;
(2)利用数轴求出这些解集的公共部分,即这个不等式组的解集.
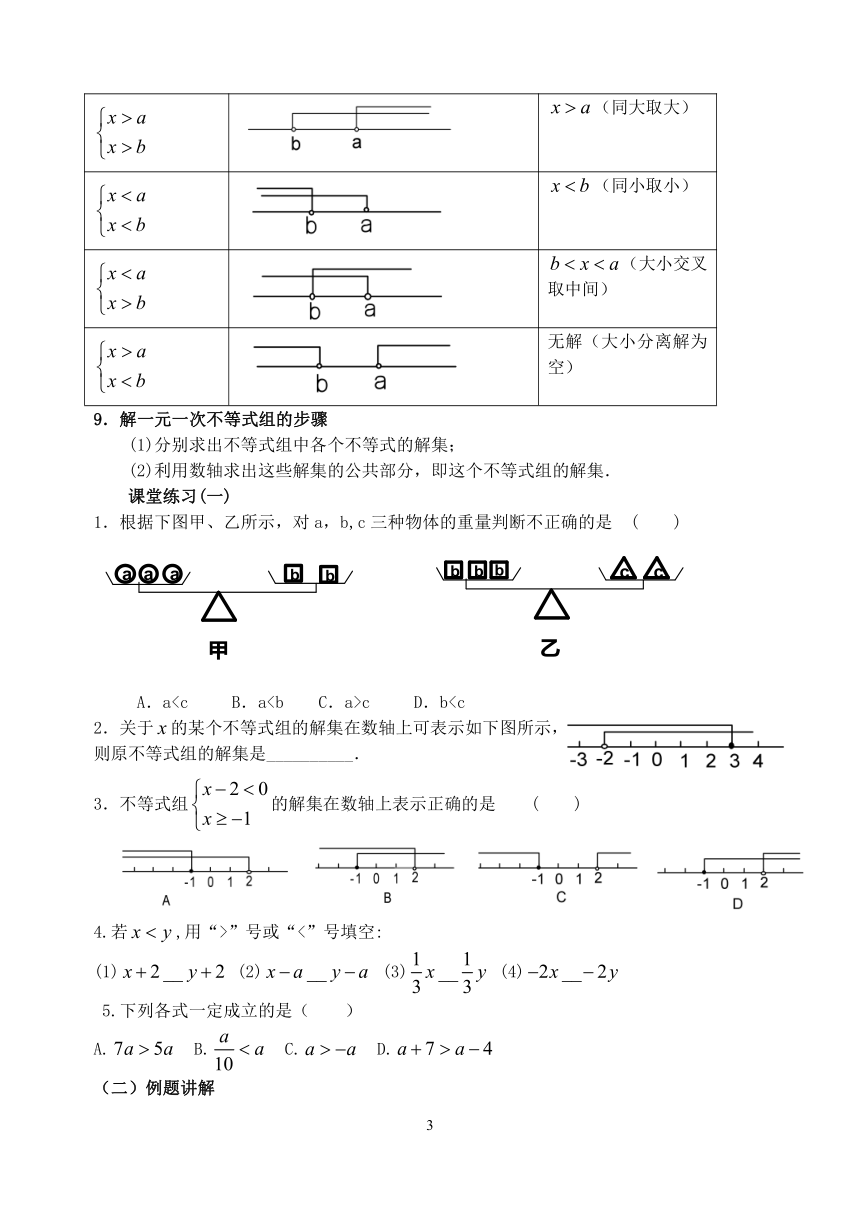
课堂练习(一)
1.根据下图甲、乙所示,对a,b,c三种物体的重量判断不正确的是 ( )
A.ac D.b2.关于的某个不等式组的解集在数轴上可表示如下图所示,
则原不等式组的解集是__________.
3.不等式组的解集在数轴上表示正确的是 ( )
4.若,用“>”号或“<”号填空:
(1) (2) (3) (4)
5.下列各式一定成立的是( )
A. B. C. D.
(二)例题讲解
【例1】解不等式:
解:去分母得
去括号得
移项得
合并同类项得
把系数化为1得
【例2】 解不等式组并把它的解集在数轴上表示出来.
解:解不等式①得
解不等式②得
不等式①和②的解集在数轴上表示为
∴原不等式组的解集是.
【例3】 已知关于的方程5-2=3-6+1的解满足-3<≤2,求的整数值.
解:由5-2=3-6+1可解得:
∵,∴.
∴ ∴
∴的整数解为0、1
课堂练习(二)
6.求代数式3(+1)的值不小于5-9的值的最大的整数.
7.解不等式组,并把它的解集在数轴上表示出来.
课堂练习(三)
8.函数的自变量的取值范围是_____________.
9.若关于的一元二次方程有两个不相等的实数根,则的取值范围为______________.
10.如果关于的不等式(a+1)>a+1的解集为 A.a>0 B.a<0 C.a>-1 D.a<-1
11.已知方程组的解满足,则( ).
A.>-1 B.>1 C.<-l D.<1
12.已知关于的不等式2+>-5的解集如图所示,则的值为( )
A.1 B.0 C.-1 D.-2
13.三角形三边长分别为3、、8,求的取值范围
14.已知关于的不等式组无解,求的取值范围.
(三)课堂小结
1.在判断不等式成立与否或由不等式变形求某些字母的范围时,要认真观察不等式的形式与不等号方向。
2.解一元一次不等式的步骤与解一元一次方程的步骤大致相同,应注意的是:①等式两边所乘以(或除以)的数的正负,并根据不同情况灵活运用其性质。②不等式组解集的确定方法。③一元一次不等式(组)常与分式、根式、方程、函数等知识联系,解决综合性问题。
3.求不等式(组)的特殊解
不等式(组)的解往往是无数多个,但有时解在某些范围内是有限的,如整数解、非负整数解,要求这些特殊解,首先是确定不等式(组)的解集,然后再找到相应的答案。在这类题目中,要注意对数形结合思想的应用。
4.确定不等式(组)中字母的取值范围
已知求不等式(组)的解集,确定不等式(组)中字母的取值范围,有以下几种方法:(1)逆用不等式(组)的解集;(2)分类讨论确定;(3)借助数轴确定。
(四)课后练习
1.已知一个等腰三角形的底边长为5,这个等腰三角形的腰长为,则的取值范围是_____________.
2.在平面直角坐标系中,点A(,)在第三象限,则的取值范围是 ( ).
A. B. C. D.
3.若关于的一元二次方程的两个实数根,且,则实数则的取值范围是( ).
A. B. C. D.
4.解不等式组:
5.求不等式组的非负整数解.
6.求使方程组的解、都是正数的的取值范围.
7.若关于的不等式组的解集为≤2,试求的取值范围.
8.你能求出三个不等式,,的解集的公共部分吗?
概念
基本性质
不等式的定义
不等式的解法
一元一次不等式
的解法
一元一次不等式组
的解法
不等式
实际应用
不等式的解集
PAGE
6
一元一次不等式与一元一次不等式组的解法
本章内容在中考中的考查方式主要是填空题、选择题及解答题中与方程、函数有关问题中字母系数的取值范围的确定.考查的重点是不等式的有关概念、性质、一元一次不等式、一元一次不等式组的解法以及与日常相联系的应用问题,在方程、函数的考查中,也常涉及不等式的知识.常结合转化、数形结合、类比、分类讨论思想方法.
一、教学目标:
1.能够根据具体问题中的大小关系了解不等式的意义和基本性质.
2.会解简单的一元一次不等式,并能在数轴上表示出解集.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集.
3.会运用数形结合、分类等数学思想方法解决问题,会“逆向”地思考问题,灵活的解答问题.
二、教学重点:能熟练的解一元一次不等式与一元一次不等式组
三、教学难点:能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想
四、教学过程
(一)知识梳理
1.知识结构图
2.知识点回顾
1.不等式
用不等号连接起来的式子叫做不等式.
常见的不等号有五种: “≠”、 “>” 、 “<” 、 “≥”、 “≤”.
2.不等式的解与解集
不等式的解:使不等式成立的未知数的值,叫做不等式的解.
不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.
不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.
3.不等式的基本性质
(1)不等式的两边都加上(或减去)同一个数或同一个整式.不等号的方向不变.如果,那么
(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.如果,那么(或)
(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.如果那么(或)
说明:任意两个实数a、b的大小关系:①a-b>Oa>b;②a-b=Oa=b;③a-b
只含有一个未知数,且未知数的次数是1.系数不等于0的不等式叫做一元一次不等式.
注:一元一次不等式的一般形式是ax+b>O或ax+b
解一元一次不等式的一般步骤:
(1)去分母;(2)去括号;(3)移项; (4)合并同类项;(5)化系数为1.
说明:解一元一次不等式和解一元一次方程类似.不同的是:一元一次不等式两边同乘以(或除以)同一个负数时,不等号的方向必须改变,这是解不等式时最容易出错的地方.
6.一元一次不等式组
含有相同未知数的几个一元一次不等式所组成的不等式组,叫做一元一次不等式组.
说明:判断一个不等式组是一元一次不等式组需满足两个条件:①组成不等式组的每一个不等式必须是一元一次不等式,且未知数相同;②不等式组中不等式的个数至少是2个,也就是说,可以是2个、3个、4个或更多.
7.一元一次不等式组的解集
一元一次不等式组中,几个不等式解集的公共部分.叫做这个一元一次不等式组的解集.
一元一次不等式组的解集通常利用数轴来确定.
8. 不等式组解集的确定方法,可以归纳为以下四种类型(设a>b)
不等式组 图示 解集
(同大取大)
(同小取小)
(大小交叉取中间)
无解(大小分离解为空)
9.解一元一次不等式组的步骤
(1)分别求出不等式组中各个不等式的解集;
(2)利用数轴求出这些解集的公共部分,即这个不等式组的解集.
课堂练习(一)
1.根据下图甲、乙所示,对a,b,c三种物体的重量判断不正确的是 ( )
A.a
则原不等式组的解集是__________.
3.不等式组的解集在数轴上表示正确的是 ( )
4.若,用“>”号或“<”号填空:
(1) (2) (3) (4)
5.下列各式一定成立的是( )
A. B. C. D.
(二)例题讲解
【例1】解不等式:
解:去分母得
去括号得
移项得
合并同类项得
把系数化为1得
【例2】 解不等式组并把它的解集在数轴上表示出来.
解:解不等式①得
解不等式②得
不等式①和②的解集在数轴上表示为
∴原不等式组的解集是.
【例3】 已知关于的方程5-2=3-6+1的解满足-3<≤2,求的整数值.
解:由5-2=3-6+1可解得:
∵,∴.
∴ ∴
∴的整数解为0、1
课堂练习(二)
6.求代数式3(+1)的值不小于5-9的值的最大的整数.
7.解不等式组,并把它的解集在数轴上表示出来.
课堂练习(三)
8.函数的自变量的取值范围是_____________.
9.若关于的一元二次方程有两个不相等的实数根,则的取值范围为______________.
10.如果关于的不等式(a+1)>a+1的解集为
11.已知方程组的解满足,则( ).
A.>-1 B.>1 C.<-l D.<1
12.已知关于的不等式2+>-5的解集如图所示,则的值为( )
A.1 B.0 C.-1 D.-2
13.三角形三边长分别为3、、8,求的取值范围
14.已知关于的不等式组无解,求的取值范围.
(三)课堂小结
1.在判断不等式成立与否或由不等式变形求某些字母的范围时,要认真观察不等式的形式与不等号方向。
2.解一元一次不等式的步骤与解一元一次方程的步骤大致相同,应注意的是:①等式两边所乘以(或除以)的数的正负,并根据不同情况灵活运用其性质。②不等式组解集的确定方法。③一元一次不等式(组)常与分式、根式、方程、函数等知识联系,解决综合性问题。
3.求不等式(组)的特殊解
不等式(组)的解往往是无数多个,但有时解在某些范围内是有限的,如整数解、非负整数解,要求这些特殊解,首先是确定不等式(组)的解集,然后再找到相应的答案。在这类题目中,要注意对数形结合思想的应用。
4.确定不等式(组)中字母的取值范围
已知求不等式(组)的解集,确定不等式(组)中字母的取值范围,有以下几种方法:(1)逆用不等式(组)的解集;(2)分类讨论确定;(3)借助数轴确定。
(四)课后练习
1.已知一个等腰三角形的底边长为5,这个等腰三角形的腰长为,则的取值范围是_____________.
2.在平面直角坐标系中,点A(,)在第三象限,则的取值范围是 ( ).
A. B. C. D.
3.若关于的一元二次方程的两个实数根,且,则实数则的取值范围是( ).
A. B. C. D.
4.解不等式组:
5.求不等式组的非负整数解.
6.求使方程组的解、都是正数的的取值范围.
7.若关于的不等式组的解集为≤2,试求的取值范围.
8.你能求出三个不等式,,的解集的公共部分吗?
概念
基本性质
不等式的定义
不等式的解法
一元一次不等式
的解法
一元一次不等式组
的解法
不等式
实际应用
不等式的解集
PAGE
6
