人教版高一物理必修二第六章万有引力与航天 6.2太阳与行星间的引力(18张PPT)
文档属性
| 名称 | 人教版高一物理必修二第六章万有引力与航天 6.2太阳与行星间的引力(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-10 21:15:55 | ||
图片预览






文档简介
(共18张PPT)
6.2太阳与行星间的引力
教学目标
1.知道行星绕太阳运动的原因,知道太阳与行星间存在着引力的作用。
2.知道行星绕太阳做匀速圆周运动的向心力的来源。
3.知道太阳与行星间引力的方向和表达式,知道牛顿定律在推导太阳与行星间引力的作用。
4.领会将不易测量的物理量转化为易测量物理量的方法。
教学重点
从动力学角度研究行星的运动
教学难点
运用已有知识进行演绎推理探究过程
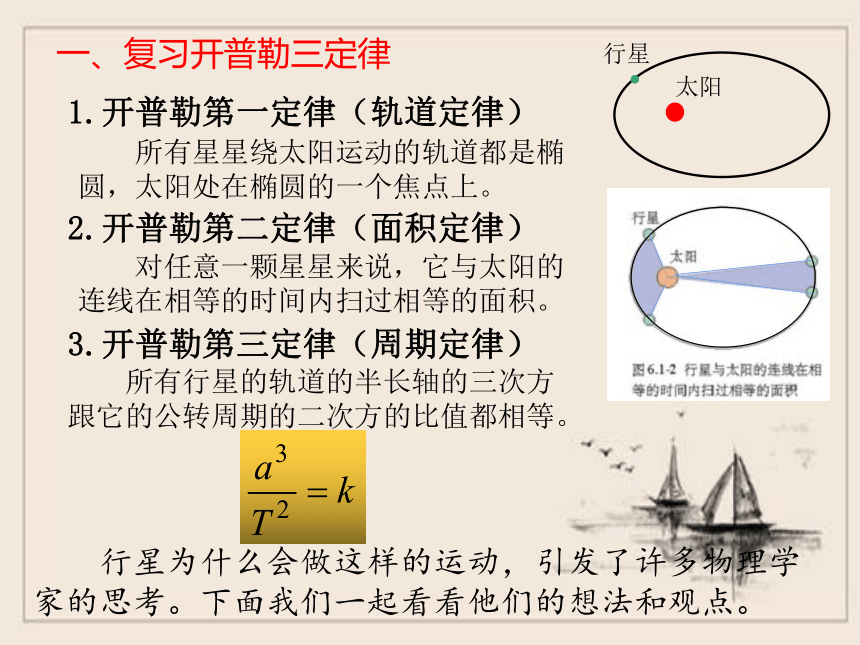
一、复习开普勒三定律
所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。
所有星星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
对任意一颗星星来说,它与太阳的连线在相等的时间内扫过相等的面积。
3.开普勒第三定律(周期定律)
2.开普勒第二定律(面积定律)
1.开普勒第一定律(轨道定律)
太阳
行星
行星为什么会做这样的运动,引发了许多物理学家的思考。下面我们一起看看他们的想法和观点。
1、伽利略
意大利物理学家、数学家、天文学家及哲学家,科学革命中的重要人物。
1564年2月15日-1642年1月8日
法国著名的哲学家、数学家、物理学家。他对现代数学的发展做出了重要的贡献,因将几何坐标体系公式化而被认为是解析几何之父。
1596年3月31日—1650年2月11日
伽利略认为:一切物体都有合并的趋势。
笛卡儿认为:在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
2、笛卡儿
二、了解物理学家的观点
1635年7月18日-1703年3月3日
牛顿对此没有复信,但接受了胡克的观点,以后在开普勒关于行星运动的第三定律基础上用数学方法导出了万有引力定律。1686年牛顿将载有万有引力定律的《自然哲学的数学原理》卷一的稿件送给英国皇家学会时,胡克希望牛顿在序言中能对他的劳动成果"提一下",但遭到牛顿的断然拒绝。
3、胡克
英国博物学家,发明家。
胡克对万有引力定律的发现起了重要作用。 1679 年他写信给牛顿,信中认为天体的运动是由于有中心引力拉住的结果,而且认为引力
与距离平方应成反比。而不象牛顿所说的,物体的轨迹是一条螺旋线,最终将绕到地心。
4、哈雷
1656年11月8日——1742年1月14日
英国天文学家、地理学家、数学家、气象学家和物理学家。
哈雷问牛顿:“要是太阳的引力与行星离太阳距离的平方成反比,你认为行星运行的曲线会是什么样的?”
牛顿回答:“会是一个椭圆。”
问:“你是怎么知道的?”
答:"我已经计算过。"
两年后牛顿拿出他的杰作《自然哲学的数学原理》,哈雷自费为他出版了这本书。
1643年1月4日—1727年3月31日
他是经典力学基础的牛顿运动定律的建立者。他发现的运动三定律和万有引力定律,为近代物理学和力学奠定了基础,他的万有引力定律和哥白尼的日心说奠定了现代天文学的理论基础。直到今天,人造地球卫星、火箭、宇宙飞船的发射升空和运行轨道的计算,都仍以此作为理论根据。
英国皇家学会会长,英国著名的物理学家,百科全书式的“全才”,著有《自然哲学的数学原理》《光学》。
5、牛顿
1687年的巨作《自然哲学的数学原理》,开辟了大科学时代。牛顿是最有影响的科学家,被誉为“物理学之父”。
是什么力来维持行星绕太阳的运动呢?
(一)、提出问题
新课教学
(二)、大胆推断
牛顿在前人对惯性研究的基础上,开始思考”物体怎样才会不沿直线运动”这一问题,他的回答是:以任何方式改变速度(包括改变速度的方向)都需要力,这就是说使行星沿圆或椭圆运动需要指向圆心或椭圆焦点的力,这个力应该就是太阳对它的引力。于是牛顿利用它的运动定律把行星的向心加速度与太阳对它的引力联系起来了。
(三)、简化模型
行星的轨道按照“圆”来处理
(四)、演绎推理
1.太阳对行星的引力
由上面的表达式可以看出太阳对行星的引力F与r的关系:
设行星的质量为m,速度为v,公转周期为T,行星到太阳的距离为r,则行星绕太阳做匀速圆周运动所需的向心力为:
结论:太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间距离的二次方成反比。
2.行星对太阳的引力
F
m
M
既然太阳对行星的引力与行星的质量m成正比,那么行星对太阳的引力是不是也跟太阳 的质量M成正比呢?
因为从太阳与行星间相互作用的角度来看,两者的地位是相同的!
3.太阳与行星间的引力
写成等式就是:
简洁的引力关系从此诞生了!
答案是肯定的!
古人观点
牛顿思考
理论演算
总结规律
理想化
课堂小结
(一)、梳理思路
(二)、梳理知识
1.太阳与行星间引力的大小与太阳、行星的质量成正比,与两者距离的二次方成反比,太阳与行星间引力的方向沿着二者的连线。
2.表达式:
式中G是比例系数,与太阳、行星都没有关系。
例题1.下面关于太阳对行星的引力的说法中正确的是( )
A.太阳对行星的引力等于行星做匀速圆周运动的向心力
B.太阳对行星的引力大小与行星的质量成正比,与行星和太阳间的距离成反比
C.太阳对行星的引力是由实验得出的
D.太阳对行星的引力规律是由开普勒定律和行星绕太阳做匀速圆周运动的规律推导出来的.
课堂练习
AD
例题2.两个行星的质量分别为m1和m2,绕太阳运行的轨道半径分别是r1和r2,若它们只受太阳引力的作用,那么这两个行星的向心加速度之比为( )
D
看到题目要求计算向心加速度之比,估计多数同学会想起向心力的几个表达式,这很正常,但发现这几个表达式都不能解决问题时,一定要学会换角度思考问题,一定要牢记,力是产生加速度的原因,以不变应万变。
练习:两颗行星质量之比m1∶m2=1∶2,轨道半径之比R1∶R2=3∶1,下列有关数据之比正确的是 ( )
A.周期之比T1∶T2=3∶1 B.线速度之比v1∶v2=3∶1
C.向心力之比F1∶F2=1∶9 D.向心加速度之比a1∶a2=1∶9
D
1.在力学中有的问题是根据物体的运动探究它受的力,另一些问题则是根据物体所受的力推测它的运动。这一节的讨论属于哪一种情况?你能从过去学过的内容或做过的练习中各找一个例子吗?
解答:这节的讨论属于根据物体的运动探究它的受力,前一章平抛运动的研究属于根据物体的受力探究它的运动,而圆周运动的研究属于根据物体的运动探究它的受力。
问题与练习
2.在探究太阳对行星的引力的规律时,我们以左边的三个等式为依据,得出了右边的关系式,左边的三个等式有的可以在实验室中验证,有的则不能,这个无法在实验室验证的规律是怎么得到的?
解答:这个无法在实验室验证的规律就是开普
勒第三定律 ,是开普勒根据研究天文
学家第谷的行星观测记录发现的。
3.自己查找月—地距离,月球公转周期等数据,计算月球公转的向心加速度,你得到的计算值相当于地面附近自由落体加速度的多少分之一?
解答:假设月地距离为r,月球公转周期为T,则月球公转的向心加速度为:
查得:r=3.8×108m,T=27.3天,代入上式可得, a=2.7×10-3m/s2。
这一数据约为g/3600,即月球公转的向心加速度约为地面附近自由落体加速度的1/3600 。
6.2太阳与行星间的引力
教学目标
1.知道行星绕太阳运动的原因,知道太阳与行星间存在着引力的作用。
2.知道行星绕太阳做匀速圆周运动的向心力的来源。
3.知道太阳与行星间引力的方向和表达式,知道牛顿定律在推导太阳与行星间引力的作用。
4.领会将不易测量的物理量转化为易测量物理量的方法。
教学重点
从动力学角度研究行星的运动
教学难点
运用已有知识进行演绎推理探究过程
一、复习开普勒三定律
所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。
所有星星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
对任意一颗星星来说,它与太阳的连线在相等的时间内扫过相等的面积。
3.开普勒第三定律(周期定律)
2.开普勒第二定律(面积定律)
1.开普勒第一定律(轨道定律)
太阳
行星
行星为什么会做这样的运动,引发了许多物理学家的思考。下面我们一起看看他们的想法和观点。
1、伽利略
意大利物理学家、数学家、天文学家及哲学家,科学革命中的重要人物。
1564年2月15日-1642年1月8日
法国著名的哲学家、数学家、物理学家。他对现代数学的发展做出了重要的贡献,因将几何坐标体系公式化而被认为是解析几何之父。
1596年3月31日—1650年2月11日
伽利略认为:一切物体都有合并的趋势。
笛卡儿认为:在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
2、笛卡儿
二、了解物理学家的观点
1635年7月18日-1703年3月3日
牛顿对此没有复信,但接受了胡克的观点,以后在开普勒关于行星运动的第三定律基础上用数学方法导出了万有引力定律。1686年牛顿将载有万有引力定律的《自然哲学的数学原理》卷一的稿件送给英国皇家学会时,胡克希望牛顿在序言中能对他的劳动成果"提一下",但遭到牛顿的断然拒绝。
3、胡克
英国博物学家,发明家。
胡克对万有引力定律的发现起了重要作用。 1679 年他写信给牛顿,信中认为天体的运动是由于有中心引力拉住的结果,而且认为引力
与距离平方应成反比。而不象牛顿所说的,物体的轨迹是一条螺旋线,最终将绕到地心。
4、哈雷
1656年11月8日——1742年1月14日
英国天文学家、地理学家、数学家、气象学家和物理学家。
哈雷问牛顿:“要是太阳的引力与行星离太阳距离的平方成反比,你认为行星运行的曲线会是什么样的?”
牛顿回答:“会是一个椭圆。”
问:“你是怎么知道的?”
答:"我已经计算过。"
两年后牛顿拿出他的杰作《自然哲学的数学原理》,哈雷自费为他出版了这本书。
1643年1月4日—1727年3月31日
他是经典力学基础的牛顿运动定律的建立者。他发现的运动三定律和万有引力定律,为近代物理学和力学奠定了基础,他的万有引力定律和哥白尼的日心说奠定了现代天文学的理论基础。直到今天,人造地球卫星、火箭、宇宙飞船的发射升空和运行轨道的计算,都仍以此作为理论根据。
英国皇家学会会长,英国著名的物理学家,百科全书式的“全才”,著有《自然哲学的数学原理》《光学》。
5、牛顿
1687年的巨作《自然哲学的数学原理》,开辟了大科学时代。牛顿是最有影响的科学家,被誉为“物理学之父”。
是什么力来维持行星绕太阳的运动呢?
(一)、提出问题
新课教学
(二)、大胆推断
牛顿在前人对惯性研究的基础上,开始思考”物体怎样才会不沿直线运动”这一问题,他的回答是:以任何方式改变速度(包括改变速度的方向)都需要力,这就是说使行星沿圆或椭圆运动需要指向圆心或椭圆焦点的力,这个力应该就是太阳对它的引力。于是牛顿利用它的运动定律把行星的向心加速度与太阳对它的引力联系起来了。
(三)、简化模型
行星的轨道按照“圆”来处理
(四)、演绎推理
1.太阳对行星的引力
由上面的表达式可以看出太阳对行星的引力F与r的关系:
设行星的质量为m,速度为v,公转周期为T,行星到太阳的距离为r,则行星绕太阳做匀速圆周运动所需的向心力为:
结论:太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间距离的二次方成反比。
2.行星对太阳的引力
F
m
M
既然太阳对行星的引力与行星的质量m成正比,那么行星对太阳的引力是不是也跟太阳 的质量M成正比呢?
因为从太阳与行星间相互作用的角度来看,两者的地位是相同的!
3.太阳与行星间的引力
写成等式就是:
简洁的引力关系从此诞生了!
答案是肯定的!
古人观点
牛顿思考
理论演算
总结规律
理想化
课堂小结
(一)、梳理思路
(二)、梳理知识
1.太阳与行星间引力的大小与太阳、行星的质量成正比,与两者距离的二次方成反比,太阳与行星间引力的方向沿着二者的连线。
2.表达式:
式中G是比例系数,与太阳、行星都没有关系。
例题1.下面关于太阳对行星的引力的说法中正确的是( )
A.太阳对行星的引力等于行星做匀速圆周运动的向心力
B.太阳对行星的引力大小与行星的质量成正比,与行星和太阳间的距离成反比
C.太阳对行星的引力是由实验得出的
D.太阳对行星的引力规律是由开普勒定律和行星绕太阳做匀速圆周运动的规律推导出来的.
课堂练习
AD
例题2.两个行星的质量分别为m1和m2,绕太阳运行的轨道半径分别是r1和r2,若它们只受太阳引力的作用,那么这两个行星的向心加速度之比为( )
D
看到题目要求计算向心加速度之比,估计多数同学会想起向心力的几个表达式,这很正常,但发现这几个表达式都不能解决问题时,一定要学会换角度思考问题,一定要牢记,力是产生加速度的原因,以不变应万变。
练习:两颗行星质量之比m1∶m2=1∶2,轨道半径之比R1∶R2=3∶1,下列有关数据之比正确的是 ( )
A.周期之比T1∶T2=3∶1 B.线速度之比v1∶v2=3∶1
C.向心力之比F1∶F2=1∶9 D.向心加速度之比a1∶a2=1∶9
D
1.在力学中有的问题是根据物体的运动探究它受的力,另一些问题则是根据物体所受的力推测它的运动。这一节的讨论属于哪一种情况?你能从过去学过的内容或做过的练习中各找一个例子吗?
解答:这节的讨论属于根据物体的运动探究它的受力,前一章平抛运动的研究属于根据物体的受力探究它的运动,而圆周运动的研究属于根据物体的运动探究它的受力。
问题与练习
2.在探究太阳对行星的引力的规律时,我们以左边的三个等式为依据,得出了右边的关系式,左边的三个等式有的可以在实验室中验证,有的则不能,这个无法在实验室验证的规律是怎么得到的?
解答:这个无法在实验室验证的规律就是开普
勒第三定律 ,是开普勒根据研究天文
学家第谷的行星观测记录发现的。
3.自己查找月—地距离,月球公转周期等数据,计算月球公转的向心加速度,你得到的计算值相当于地面附近自由落体加速度的多少分之一?
解答:假设月地距离为r,月球公转周期为T,则月球公转的向心加速度为:
查得:r=3.8×108m,T=27.3天,代入上式可得, a=2.7×10-3m/s2。
这一数据约为g/3600,即月球公转的向心加速度约为地面附近自由落体加速度的1/3600 。
