沪科版九下数学24.1.3 中心对称图形 习题课件(30张PPT)
文档属性
| 名称 | 沪科版九下数学24.1.3 中心对称图形 习题课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-11 22:26:24 | ||
图片预览







文档简介
(共30张PPT)
第24章 圆
24.1 旋转
中心对称图形
1
知识点
中心对称图形的定义
1.下列汽车标志中,可以看成中心对称图形的是( )
D
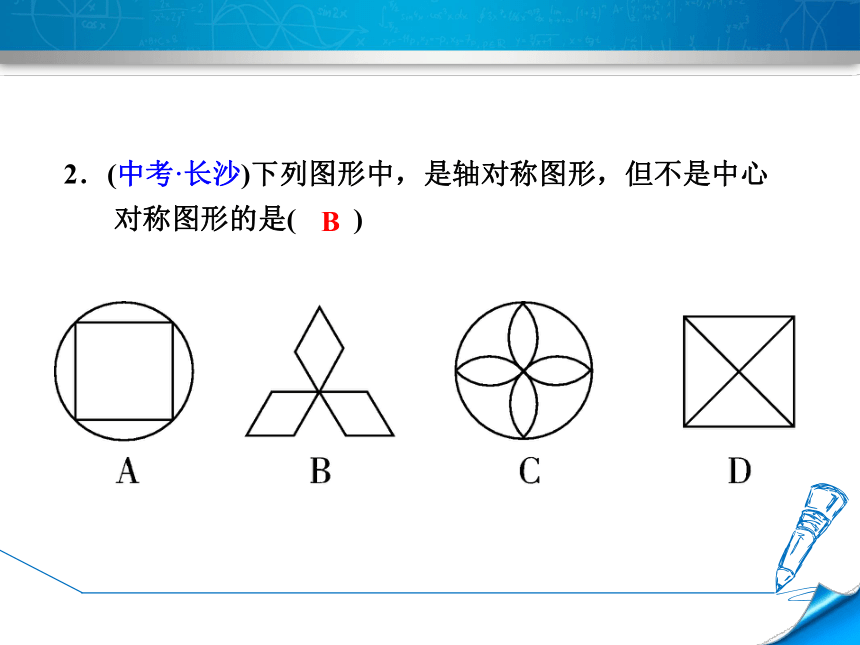
2.(中考·长沙)下列图形中,是轴对称图形,但不是中心
对称图形的是( )
B
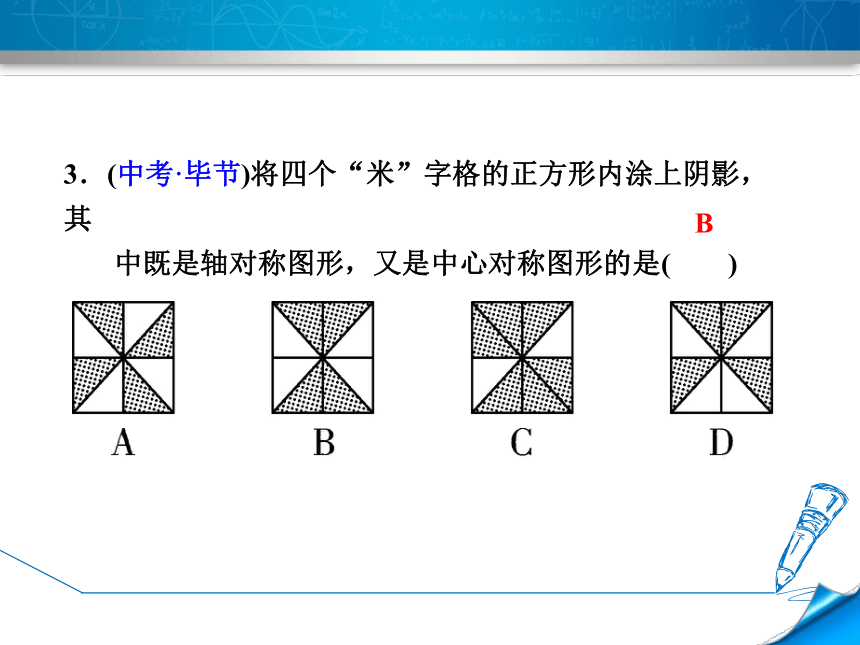
3.(中考·毕节)将四个“米”字格的正方形内涂上阴影,其
中既是轴对称图形,又是中心对称图形的是( )
B
4.如图,对其对称性描述正确的是( )
A.轴对称图形
B.中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形又不是中心对称图形
B
5.(中考·无锡)下列图形中,是轴对称图形但不是中心对称图
形的是( )
A.等边三角形
B.平行四边形
C.矩形
D.圆
A
2
知识点
中心对称图形的性质
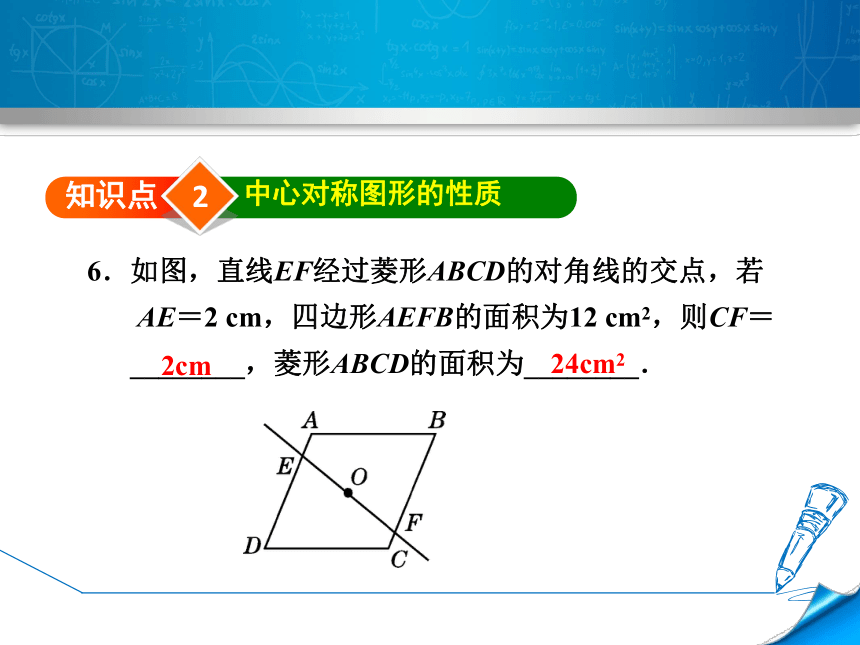
6.如图,直线EF经过菱形ABCD的对角线的交点,若
AE=2 cm,四边形AEFB的面积为12 cm2,则CF=
________,菱形ABCD的面积为________.
2cm
24cm2
7.仔细观察艺术字: 一,与这些字具有相同对称特
征的汉字是( )
A.甲 B.土 C.日 D.木
C
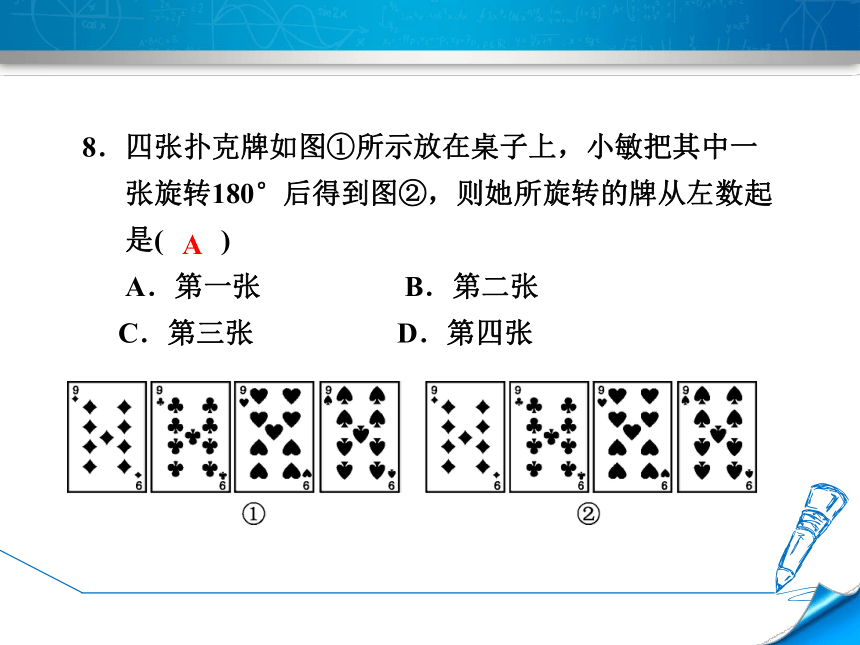
8.四张扑克牌如图①所示放在桌子上,小敏把其中一
张旋转180°后得到图②,则她所旋转的牌从左数起
是( )
A.第一张 B.第二张
C.第三张 D.第四张
A
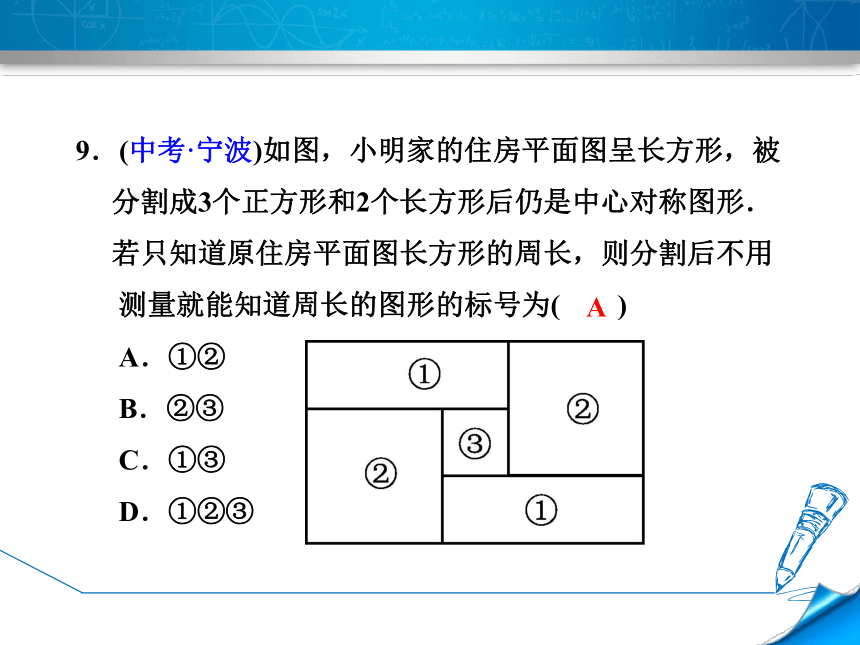
9.(中考·宁波)如图,小明家的住房平面图呈长方形,被
分割成3个正方形和2个长方形后仍是中心对称图形.
若只知道原住房平面图长方形的周长,则分割后不用
测量就能知道周长的图形的标号为( )
A.①②
B.②③
C.①③
D.①②③
A
如图,设图形①的长和宽分别是a、c,图形②的边长是b,图形③的边长是d,原来大长方形的周长是l,则l=2(a+2b+c),
根据图示,
可得
(1)-(2),可得a-b=b-c,∴2b=a+c.
∴l=2(a+2b+c)=2×2(a+c)=4(a+c),或l=2(a+2b+c)=2×4b=8b.
∴2(a+c)= ,4b= .
∵图形①的周长是2(a+c),图形②的周长是4b, 的值
一定,
∴图形①②的周长是定值,不用测量就能知道,图形③的周长不用测量无法知道.
∴分割后不用测量就能知道周长的图形的标号为①②.
10.如图,已知四边形ABCD是菱形,点B(0,6),点
C(-8,0),E是AB的中点,则直线DE的解析式为
( )
A.y= x-6
B.y= x+6
C.y= x-6
D.y= x+6
C
3
知识点
中心对称图形的作图
11.(1)(中考·枣庄)如图,在方格纸中,选择标有序号
①②③④的小正方形中的一个涂黑,与图中阴影部
分构成中心对称图形,该小正方形的序号是( )
A.①
B.②
C.③
D.④
B
(2)如图是某种标志的一部分,已知该标志是中心对称
图形,其对称中心是点A,请补全图形.
解:如图所示.
12.如图,矩形ABCD是篮球场的简图,请通过画图找出
它的对称中心.
解:作图略,连接AC,BD,它们的交点就是对称
中心.
1
易错点
对中心对称图形识别不清
13.有下列图形:①线段,②三角形,③平行四边形,
④正方形,⑤圆,⑥等腰梯形.其中不是中心对称
图形的是________(填序号).
②⑥
错解:①②③
诊断:错解的原因是对一些常见的图形不能正确分析.根据中心对称图形的概念,可知线段绕其中点旋转180°,平行四边形绕其对角线的交点旋转180°,正方形绕其对角线的交点旋转180°,圆绕其圆心旋转180°,都能与自身重合,都是中心对称图形,只有三角形和等腰梯形,找不到对称中心,故不是中心对称图形.
名师点金
判断中心对称图形的“两个方法”:
(1)若一个图形上,存在这样的一个点,使整个图形绕
着这个点旋转180°后能够与原来的图形重合,则这
个图形就是中心对称图形.
(2)若图形中的对应点的连线都经过同一个点,并且被
这个点平分,则这个图形就是中心对称图形.
1
考查角度
利用对称图形的性质作图
14.如图,方格纸中有三个点A,B,C,要求作一个四
边形使这三个点在这个四边形的边(包括顶点)上,
且四边形的顶点在方格的顶点上.
(1)在图①中作出的四边形是中
心对称图形但不是轴对称图
形;
(2)在图②中作出的四边形是轴对称图形但不是中心对
称图形;
(3)在图③中作出的四边形既是轴对称图形又是中心对
称图形.
解:本题答案不唯一,如图:
2
考查角度
利用中心对称图形的性质等分面积
15.如图所示,一块木板的所有拐角都是直角,一木工
想要将它锯成面积相等的两块,请你帮他设计出一
种简单的方法,画出一条线,使这条线将木板分成
面积相等的两部分.(画出必要的辅助线)
过中心对称图形的对称中心的任意一条直线都能把图形分成面积相等的两部分.
解:如图所示的三种方法均可.
3
考查角度
利用中心对称的性质在图形上作成中心对称的图形
16.如图,已知O是 ABCD对角线AC的中点,M是OA
上任意一点(M不与O,A重合).
(1)画一个与△DAM关于点O成中心对称的△BCN;
(2)画一个与△DCM关于点O成中心对称的图形;
(3)连接DN,BM,试判断图
中还有几个平行四边形.
(1)在OC上截取ON=OM,连接BN,
则△BCN与 △DAM关于点O中心对称.
(2)△BAN与△DCM关于点O成中心对称.
(3)还有一个,即 DMBN.
解:
1
拔尖角度
利用旋转方法作图并判断所作图形的形状
17.已知AB在平面直角坐标系中的位置如图所示,每个
小正方形的边长是1.
(1)在x轴上找一点C,画出
△ABC,使△ABC是以
AB为底的等腰三角形,
并写出点C的坐标:________;
(0,0)
解:
(1)画图略.
(2)将△ABC绕着点C分别按逆时针方向旋转90°、180°、
270°,画出旋转后的图形;
(3)试欣赏你画出的整个图形,想一想,整个图形是否是轴
对称图形?若是,有多少条对称轴?整个图形是否是中
心对称图形?若是,对称中心是什么?
(2)图略.
(3)整个图形是轴对称图形,有四条对称轴;整个图形
是中心对称图形,对称中心是原点.
2
拔尖角度
利用图形变换的性质求相关点的坐标
18.如图所示,在平面直角坐标系中,Rt△ABC的三个
顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转
后对应的△A1B1C;平移△ABC,
若点A的对应点A2的坐标为
(0,-4),画出平移后对应
的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直
接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写
出点P的坐标.
(1)画出△A1B1C和△A2B2C2
如图所示.
(2)旋转中心的坐标为
(3)点P的坐标为(-2,0).
解题策略:本题考查的是旋转变换及平移变换,解题的关键是作图要准确.
解:
第24章 圆
24.1 旋转
中心对称图形
1
知识点
中心对称图形的定义
1.下列汽车标志中,可以看成中心对称图形的是( )
D
2.(中考·长沙)下列图形中,是轴对称图形,但不是中心
对称图形的是( )
B
3.(中考·毕节)将四个“米”字格的正方形内涂上阴影,其
中既是轴对称图形,又是中心对称图形的是( )
B
4.如图,对其对称性描述正确的是( )
A.轴对称图形
B.中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形又不是中心对称图形
B
5.(中考·无锡)下列图形中,是轴对称图形但不是中心对称图
形的是( )
A.等边三角形
B.平行四边形
C.矩形
D.圆
A
2
知识点
中心对称图形的性质
6.如图,直线EF经过菱形ABCD的对角线的交点,若
AE=2 cm,四边形AEFB的面积为12 cm2,则CF=
________,菱形ABCD的面积为________.
2cm
24cm2
7.仔细观察艺术字: 一,与这些字具有相同对称特
征的汉字是( )
A.甲 B.土 C.日 D.木
C
8.四张扑克牌如图①所示放在桌子上,小敏把其中一
张旋转180°后得到图②,则她所旋转的牌从左数起
是( )
A.第一张 B.第二张
C.第三张 D.第四张
A
9.(中考·宁波)如图,小明家的住房平面图呈长方形,被
分割成3个正方形和2个长方形后仍是中心对称图形.
若只知道原住房平面图长方形的周长,则分割后不用
测量就能知道周长的图形的标号为( )
A.①②
B.②③
C.①③
D.①②③
A
如图,设图形①的长和宽分别是a、c,图形②的边长是b,图形③的边长是d,原来大长方形的周长是l,则l=2(a+2b+c),
根据图示,
可得
(1)-(2),可得a-b=b-c,∴2b=a+c.
∴l=2(a+2b+c)=2×2(a+c)=4(a+c),或l=2(a+2b+c)=2×4b=8b.
∴2(a+c)= ,4b= .
∵图形①的周长是2(a+c),图形②的周长是4b, 的值
一定,
∴图形①②的周长是定值,不用测量就能知道,图形③的周长不用测量无法知道.
∴分割后不用测量就能知道周长的图形的标号为①②.
10.如图,已知四边形ABCD是菱形,点B(0,6),点
C(-8,0),E是AB的中点,则直线DE的解析式为
( )
A.y= x-6
B.y= x+6
C.y= x-6
D.y= x+6
C
3
知识点
中心对称图形的作图
11.(1)(中考·枣庄)如图,在方格纸中,选择标有序号
①②③④的小正方形中的一个涂黑,与图中阴影部
分构成中心对称图形,该小正方形的序号是( )
A.①
B.②
C.③
D.④
B
(2)如图是某种标志的一部分,已知该标志是中心对称
图形,其对称中心是点A,请补全图形.
解:如图所示.
12.如图,矩形ABCD是篮球场的简图,请通过画图找出
它的对称中心.
解:作图略,连接AC,BD,它们的交点就是对称
中心.
1
易错点
对中心对称图形识别不清
13.有下列图形:①线段,②三角形,③平行四边形,
④正方形,⑤圆,⑥等腰梯形.其中不是中心对称
图形的是________(填序号).
②⑥
错解:①②③
诊断:错解的原因是对一些常见的图形不能正确分析.根据中心对称图形的概念,可知线段绕其中点旋转180°,平行四边形绕其对角线的交点旋转180°,正方形绕其对角线的交点旋转180°,圆绕其圆心旋转180°,都能与自身重合,都是中心对称图形,只有三角形和等腰梯形,找不到对称中心,故不是中心对称图形.
名师点金
判断中心对称图形的“两个方法”:
(1)若一个图形上,存在这样的一个点,使整个图形绕
着这个点旋转180°后能够与原来的图形重合,则这
个图形就是中心对称图形.
(2)若图形中的对应点的连线都经过同一个点,并且被
这个点平分,则这个图形就是中心对称图形.
1
考查角度
利用对称图形的性质作图
14.如图,方格纸中有三个点A,B,C,要求作一个四
边形使这三个点在这个四边形的边(包括顶点)上,
且四边形的顶点在方格的顶点上.
(1)在图①中作出的四边形是中
心对称图形但不是轴对称图
形;
(2)在图②中作出的四边形是轴对称图形但不是中心对
称图形;
(3)在图③中作出的四边形既是轴对称图形又是中心对
称图形.
解:本题答案不唯一,如图:
2
考查角度
利用中心对称图形的性质等分面积
15.如图所示,一块木板的所有拐角都是直角,一木工
想要将它锯成面积相等的两块,请你帮他设计出一
种简单的方法,画出一条线,使这条线将木板分成
面积相等的两部分.(画出必要的辅助线)
过中心对称图形的对称中心的任意一条直线都能把图形分成面积相等的两部分.
解:如图所示的三种方法均可.
3
考查角度
利用中心对称的性质在图形上作成中心对称的图形
16.如图,已知O是 ABCD对角线AC的中点,M是OA
上任意一点(M不与O,A重合).
(1)画一个与△DAM关于点O成中心对称的△BCN;
(2)画一个与△DCM关于点O成中心对称的图形;
(3)连接DN,BM,试判断图
中还有几个平行四边形.
(1)在OC上截取ON=OM,连接BN,
则△BCN与 △DAM关于点O中心对称.
(2)△BAN与△DCM关于点O成中心对称.
(3)还有一个,即 DMBN.
解:
1
拔尖角度
利用旋转方法作图并判断所作图形的形状
17.已知AB在平面直角坐标系中的位置如图所示,每个
小正方形的边长是1.
(1)在x轴上找一点C,画出
△ABC,使△ABC是以
AB为底的等腰三角形,
并写出点C的坐标:________;
(0,0)
解:
(1)画图略.
(2)将△ABC绕着点C分别按逆时针方向旋转90°、180°、
270°,画出旋转后的图形;
(3)试欣赏你画出的整个图形,想一想,整个图形是否是轴
对称图形?若是,有多少条对称轴?整个图形是否是中
心对称图形?若是,对称中心是什么?
(2)图略.
(3)整个图形是轴对称图形,有四条对称轴;整个图形
是中心对称图形,对称中心是原点.
2
拔尖角度
利用图形变换的性质求相关点的坐标
18.如图所示,在平面直角坐标系中,Rt△ABC的三个
顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转
后对应的△A1B1C;平移△ABC,
若点A的对应点A2的坐标为
(0,-4),画出平移后对应
的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直
接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写
出点P的坐标.
(1)画出△A1B1C和△A2B2C2
如图所示.
(2)旋转中心的坐标为
(3)点P的坐标为(-2,0).
解题策略:本题考查的是旋转变换及平移变换,解题的关键是作图要准确.
解:
