2019-2020学年高中数学新同步苏教版必修2学案:第2章2.32.3.2 空间两点间的距离Word版含解析
文档属性
| 名称 | 2019-2020学年高中数学新同步苏教版必修2学案:第2章2.32.3.2 空间两点间的距离Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 295.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览


文档简介
2.3.2 空间两点间的距离
学 习 目 标
核 心 素 养
1.了解由特殊到一般推导空间两点间的距离公式的过程.(重点)
2.会应用空间两点间的距离公式求空间中的两点间的距离.(难点)
通过学习本节内容提升学生的直观想象、数学运算核心素养.
1.空间两点间的距离公式
(1)平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的距离为P1P2=.特别地,点A(x,y)到原点距离为OA=.
(2)空间两点P1(x1,y1,z1),P2(x2,y2,z2)的距离公式是P1P2=.特别地,点A(x,y,z)到原点的距离公式为OA=.
2.空间两点的中点坐标公式
连结空间两点P1(x1,y1,z1),P2(x2,y2,z2)的线段P1P2的中点M的坐标为.
1.点P(-2,-1,1)到原点的距离为________.
[PO==.]
2.给定空间直角坐标系,在x轴上找一点P,使它与点P0(4,1,2)的距离为,则该点的坐标为__________.
(9,0,0)或(-1,0,0) [设点P的坐标是(x,0,0),由题意得,P0P=,即=,∴(x-4)2=25,解得x=9或x=-1.
∴点P的坐标为(9,0,0)或(-1,0,0).]
3.若O为原点,P点坐标为(2,-4,-6),Q为OP中点,那么Q点的坐标为________.
(1,-2,-3) [设Q(x,y,z),
则x==1,y==-2,
z==-3,
∴Q(1,-2,-3).]
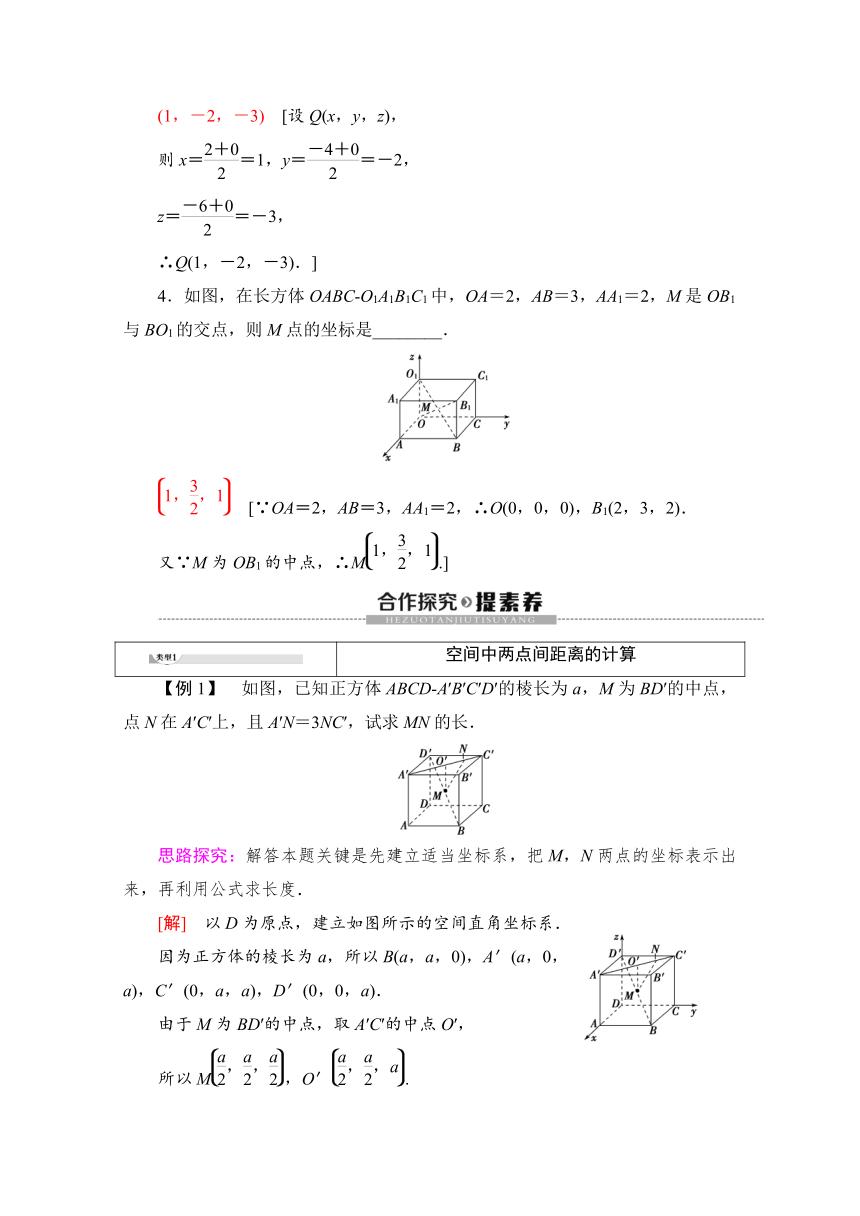
4.如图,在长方体OABC-O1A1B1C1中,OA=2,AB=3,AA1=2,M是OB1与BO1的交点,则M点的坐标是________.
[∵OA=2,AB=3,AA1=2,∴O(0,0,0),B1(2,3,2).
又∵M为OB1的中点,∴M.]
空间中两点间距离的计算
【例1】 如图,已知正方体ABCD-A′B′C′D′的棱长为a,M为BD′的中点,点N在A′C′上,且A′N=3NC′,试求MN的长.
思路探究:解答本题关键是先建立适当坐标系,把M,N两点的坐标表示出来,再利用公式求长度.
[解] 以D为原点,建立如图所示的空间直角坐标系.
因为正方体的棱长为a,所以B(a,a,0),A′(a,0,a),C′(0,a,a),D′(0,0,a).
由于M为BD′的中点,取A′C′的中点O′,
所以M,O′.
因为A′N=3NC′,所以N为A′C′的四等分点,从而N为O′C′的中点,故N,根据空间两点距离公式,可得
MN==a.
利用空间两点间的距离公式求空间两点间距离的步骤
(1)建立适当的坐标系,并写出相关点的坐标;
(2)代入空间两点间的距离公式求值.
1.已知△ABC的三个顶点A(1,5,2),B(2,3,4),C(3,1,5).
(1)求△ABC中最短边的边长;
(2)求AC边上中线的长度.
[解] (1)由空间两点间距离公式得
AB==3,
BC==,
AC==,
∴△ABC中最短边是BC,其长度为.
(2)由中点坐标公式得,AC的中点坐标为.
∴AC边上中线的长度为
=.
确定空间点的坐标
[探究问题]
1.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是什么?
[提示] 设M(0,a,0),由已知得MA=MB,即=,解得a=-1,故M(0,-1,0).
2.方程(x-1)2+(y-2)2+(z-3)2=25的几何意义是什么?
[提示] 依题意=5,点(x,y,z)是空间中到点(1,2,3)距离等于5的点,即以点(1,2,3)为球心,以5为半径的球面.
【例2】 已知A(x,5-x,2x-1),B(1,x+2,2-x),求AB取最小值时A,B两点的坐标,并求此时的AB的长度.
思路探究:解答本题可由空间两点间的距离公式建立AB关于x的函数,由函数的性质求x,再确定坐标.
[解] 由空间两点间的距离公式得AB=
=
=,
当x=时 ,AB有最小值=,
此时A,B.
解决这类问题的关键是根据点的坐标的特征,应用空间两点间的距离公式建立已知与未知的关系,再结合已知条件确定点的坐标.
2.如图所示,正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0(1)求MN的长;
(2)当a为何值时,MN的长最小.
[解] 以B为坐标原点,BA,BE,BC所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示.
∵正方形ABCD,ABEF的边长都是1,且CM=BN=a(0∴易得点M,N的坐标分别为
M,
N.
(1)|MN|=
=(0(2)∵MN==,
∴当a=时,MN的长最小,且最小值为.
1.本节课的重点是理解空间两点间距离公式的推导过程和方法,掌握空间两点间的距离公式和中点坐标公式及其简单应用.难点是空间直角坐标系的恰当建立及求相关点的坐标.
2.本节课要重点掌握的规律方法
(1)求空间中对称点坐标的规律.
(2)空间两点间距离公式的应用.
3.本节课的易错点是空间两点间距离的求解运算.
1.已知A(1,1,1),B(-3,-3,-3),则线段AB的长为( )
A.4 B.2
C.4 D.3
A [AB==4.]
2.已知△ABC三个顶点的坐标分别为A(3,1,2),B(4,-2,-2),C(0,5,1),则BC边上的中线长为________.
[∵B(4,-2,-2),C(0,5,1),
∴BC的中点为,
∴BC边上的中线长为
=.]
3.已知点A(x,1,2)和点B(2,3,4),且AB=2,则实数x的值是________.
-2或6 [由题意得
=2,
解得x=-2或x=6.]
4.已知A(1,-2,11),B(4,2,3),C(6,-1,4)为三角形的三个顶点,求证:三角形ABC为直角三角形.
[证明] 由空间两点间的距离公式得
AB==,
BC==,
AC==,
∵AB2=BC2+AC2,
∴△ABC为直角三角形,∠C为直角.
学 习 目 标
核 心 素 养
1.了解由特殊到一般推导空间两点间的距离公式的过程.(重点)
2.会应用空间两点间的距离公式求空间中的两点间的距离.(难点)
通过学习本节内容提升学生的直观想象、数学运算核心素养.
1.空间两点间的距离公式
(1)平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的距离为P1P2=.特别地,点A(x,y)到原点距离为OA=.
(2)空间两点P1(x1,y1,z1),P2(x2,y2,z2)的距离公式是P1P2=.特别地,点A(x,y,z)到原点的距离公式为OA=.
2.空间两点的中点坐标公式
连结空间两点P1(x1,y1,z1),P2(x2,y2,z2)的线段P1P2的中点M的坐标为.
1.点P(-2,-1,1)到原点的距离为________.
[PO==.]
2.给定空间直角坐标系,在x轴上找一点P,使它与点P0(4,1,2)的距离为,则该点的坐标为__________.
(9,0,0)或(-1,0,0) [设点P的坐标是(x,0,0),由题意得,P0P=,即=,∴(x-4)2=25,解得x=9或x=-1.
∴点P的坐标为(9,0,0)或(-1,0,0).]
3.若O为原点,P点坐标为(2,-4,-6),Q为OP中点,那么Q点的坐标为________.
(1,-2,-3) [设Q(x,y,z),
则x==1,y==-2,
z==-3,
∴Q(1,-2,-3).]
4.如图,在长方体OABC-O1A1B1C1中,OA=2,AB=3,AA1=2,M是OB1与BO1的交点,则M点的坐标是________.
[∵OA=2,AB=3,AA1=2,∴O(0,0,0),B1(2,3,2).
又∵M为OB1的中点,∴M.]
空间中两点间距离的计算
【例1】 如图,已知正方体ABCD-A′B′C′D′的棱长为a,M为BD′的中点,点N在A′C′上,且A′N=3NC′,试求MN的长.
思路探究:解答本题关键是先建立适当坐标系,把M,N两点的坐标表示出来,再利用公式求长度.
[解] 以D为原点,建立如图所示的空间直角坐标系.
因为正方体的棱长为a,所以B(a,a,0),A′(a,0,a),C′(0,a,a),D′(0,0,a).
由于M为BD′的中点,取A′C′的中点O′,
所以M,O′.
因为A′N=3NC′,所以N为A′C′的四等分点,从而N为O′C′的中点,故N,根据空间两点距离公式,可得
MN==a.
利用空间两点间的距离公式求空间两点间距离的步骤
(1)建立适当的坐标系,并写出相关点的坐标;
(2)代入空间两点间的距离公式求值.
1.已知△ABC的三个顶点A(1,5,2),B(2,3,4),C(3,1,5).
(1)求△ABC中最短边的边长;
(2)求AC边上中线的长度.
[解] (1)由空间两点间距离公式得
AB==3,
BC==,
AC==,
∴△ABC中最短边是BC,其长度为.
(2)由中点坐标公式得,AC的中点坐标为.
∴AC边上中线的长度为
=.
确定空间点的坐标
[探究问题]
1.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是什么?
[提示] 设M(0,a,0),由已知得MA=MB,即=,解得a=-1,故M(0,-1,0).
2.方程(x-1)2+(y-2)2+(z-3)2=25的几何意义是什么?
[提示] 依题意=5,点(x,y,z)是空间中到点(1,2,3)距离等于5的点,即以点(1,2,3)为球心,以5为半径的球面.
【例2】 已知A(x,5-x,2x-1),B(1,x+2,2-x),求AB取最小值时A,B两点的坐标,并求此时的AB的长度.
思路探究:解答本题可由空间两点间的距离公式建立AB关于x的函数,由函数的性质求x,再确定坐标.
[解] 由空间两点间的距离公式得AB=
=
=,
当x=时 ,AB有最小值=,
此时A,B.
解决这类问题的关键是根据点的坐标的特征,应用空间两点间的距离公式建立已知与未知的关系,再结合已知条件确定点的坐标.
2.如图所示,正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0
(2)当a为何值时,MN的长最小.
[解] 以B为坐标原点,BA,BE,BC所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示.
∵正方形ABCD,ABEF的边长都是1,且CM=BN=a(0
M,
N.
(1)|MN|=
=(0
∴当a=时,MN的长最小,且最小值为.
1.本节课的重点是理解空间两点间距离公式的推导过程和方法,掌握空间两点间的距离公式和中点坐标公式及其简单应用.难点是空间直角坐标系的恰当建立及求相关点的坐标.
2.本节课要重点掌握的规律方法
(1)求空间中对称点坐标的规律.
(2)空间两点间距离公式的应用.
3.本节课的易错点是空间两点间距离的求解运算.
1.已知A(1,1,1),B(-3,-3,-3),则线段AB的长为( )
A.4 B.2
C.4 D.3
A [AB==4.]
2.已知△ABC三个顶点的坐标分别为A(3,1,2),B(4,-2,-2),C(0,5,1),则BC边上的中线长为________.
[∵B(4,-2,-2),C(0,5,1),
∴BC的中点为,
∴BC边上的中线长为
=.]
3.已知点A(x,1,2)和点B(2,3,4),且AB=2,则实数x的值是________.
-2或6 [由题意得
=2,
解得x=-2或x=6.]
4.已知A(1,-2,11),B(4,2,3),C(6,-1,4)为三角形的三个顶点,求证:三角形ABC为直角三角形.
[证明] 由空间两点间的距离公式得
AB==,
BC==,
AC==,
∵AB2=BC2+AC2,
∴△ABC为直角三角形,∠C为直角.
