人教版高二物理选修3-3第八章气体 8.1 气体的等温变化之气体压强的计算(17张PPT)课件
文档属性
| 名称 | 人教版高二物理选修3-3第八章气体 8.1 气体的等温变化之气体压强的计算(17张PPT)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 463.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-11 19:24:07 | ||
图片预览



文档简介
(共17张PPT)
8.1 气体的等温变化(2)
专题:封闭气体压强的计算
学习目标:
掌握封闭气体压强的计算方法。
思考:
1:压强的定义及定义式是怎样的?
2:气体的压强是如何产生的?
3:封闭在容器中的气体的压强如何计算?
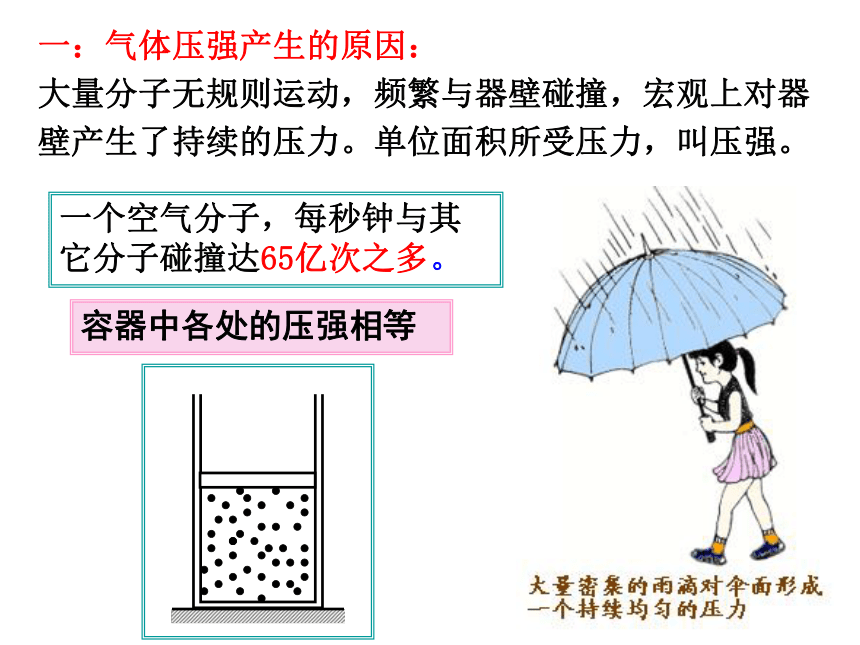
一:气体压强产生的原因:
大量分子无规则运动,频繁与器壁碰撞,宏观上对器壁产生了持续的压力。单位面积所受压力,叫压强。
一个空气分子,每秒钟与其它分子碰撞达65亿次之多。
容器中各处的压强相等
1. 理论依据
(1)液体压强的计算公式 p = ?gh。
(2)液面与外界大气相接触,则液面下h处的压强为 p = p0 + ?gh
(3)连通器原理:在连通器中,同一种液体(中间液体不间断)的同一水平面上的压强是相等的。
二、平衡态下液体封闭气体压强的计算
(1)连通器原理:根据同种液体在同一水平液面处压强相等,在连通器内灵活选取等压面.由两侧压强相等列方程求解压强.
例如图中,同一液面C、D处压强相等pA=p0+ph.
(2)参考液片法:选取假想的液体薄片(自身重力不计)为研究对象,分析液片两侧受力情况,建立平衡方程消去面积,得到液片两侧压强相等,进而求得气体压强.
例如,图中粗细均匀的U形管中封闭了一定质量的气体A,在其最低处取一液片B,由其两侧受力平衡可知
(pA+ph0)S=(p0+ph+ph0)S.即pA=p0+ph.
2.计算方法
(3)受力平衡法:选与封闭气体接触的液柱为研究对象进行受力分析,由F合=0列式求气体压强.
①
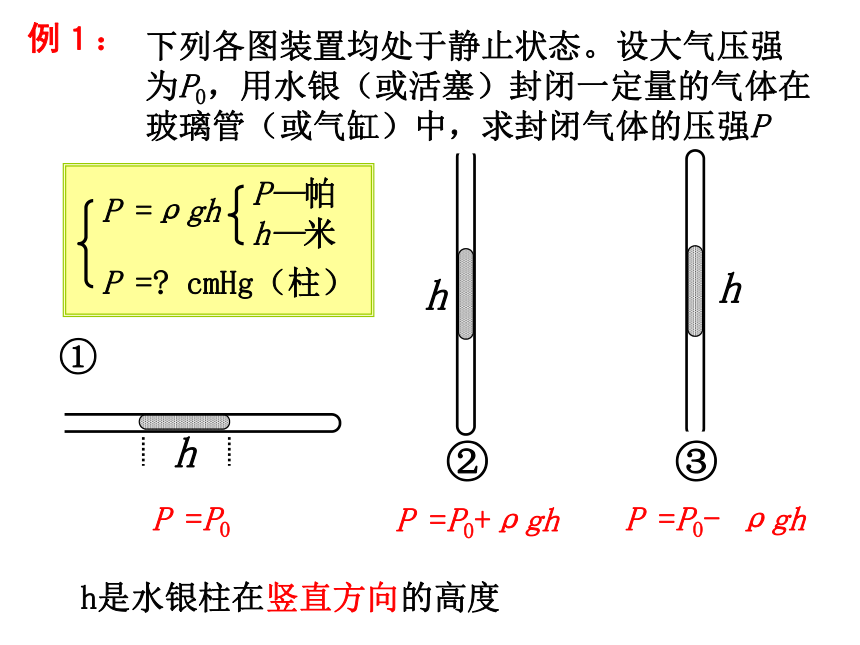
下列各图装置均处于静止状态。设大气压强为P0,用水银(或活塞)封闭一定量的气体在玻璃管(或气缸)中,求封闭气体的压强P
例1:
P =P0
P =P0+ρgh
P =P0- ρgh
h是水银柱在竖直方向的高度
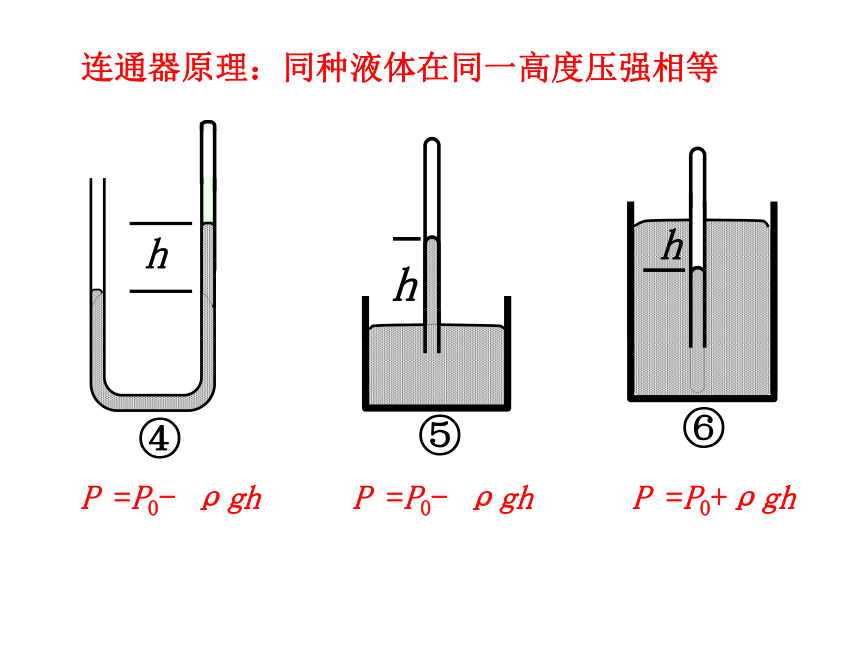
连通器原理:同种液体在同一高度压强相等
P =P0+ρgh
P =P0- ρgh
P =P0- ρgh
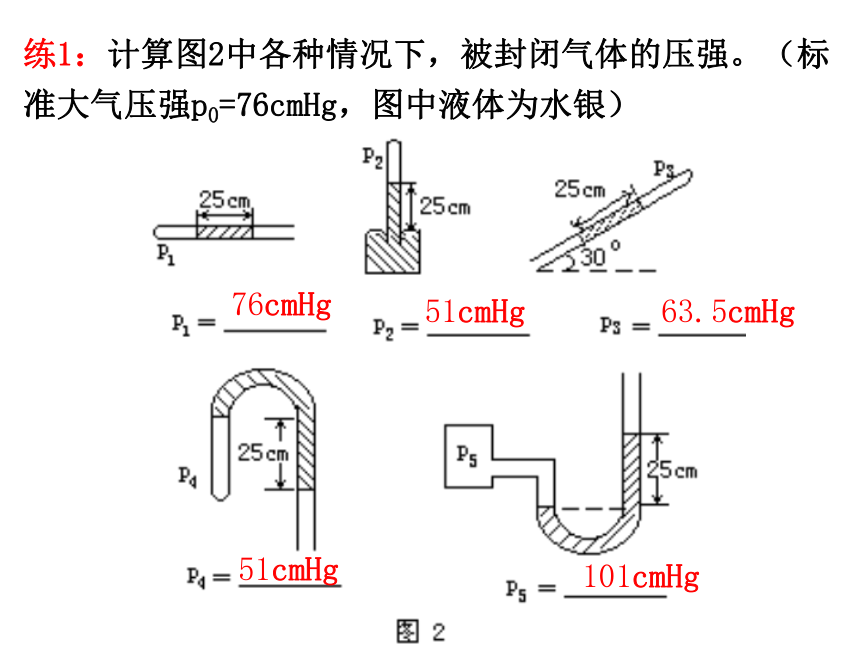
练1:计算图2中各种情况下,被封闭气体的压强。(标准大气压强p0=76cmHg,图中液体为水银)
76cmHg
51cmHg
63.5cmHg
51cmHg
101cmHg
气体对面的压力与面垂直: F=PS
PS = P0S+mg
S′
PS =mg +P0S'cosθ
PS = mg+P0S
三、平衡态下固体密闭气体压强的计算
以活塞为研究对象
以气缸为研究对象
mg+PS = P0S
Mg+PS = P0S
练2:三个长方体容器中被光滑的活塞封闭一定质量的气体。如图3所示,M为重物质量,F是外力,p0为大气压,S为活塞面积,G为活塞重,则压强各为:
四、非平衡态下固体,液体闭气体压强的计算
当封闭气体的所在的系统处于力学非平衡状态时,欲求封闭气体压强,首先要选择 恰当的对象(如与气体相关的液体、活塞等)并对其进行正确的受力分析(特别注意分析内外的压力)然后应用牛顿第二定律列方程求解。
解得:P =P0+ρ(g-a)h
解:对液体柱,由牛顿第二定律得
P0S+mg-PS =ma
m=?hs
练3:如下图甲所示,气缸质量为m1,活塞质量为m2,不计缸内气体的质量及一切摩擦,当用一水平外力F拉活塞时,活塞和气缸最终以共同的加速度运动.求此时缸内气体的压强.(已知大气压为p0,活塞横截面积为S)
解:以气缸整体为研究对象,F=(m1+m2)a
以m2为研究对象,如图乙:F-P0S+PS=m2a
类型
1、液体密封气体
2、容器密封气体
3、气缸密封气体
课堂小结:
思路方法步骤
1、定对象
2、分析力
3、用规律
整体
部分
缸体
活塞
密封气体
静态∑F外=0
动态∑F外=ma
1.已知大气压强为p0,如图所示,竖直的U形管内A、B两部分被水银柱密封着,则两部分气体的压强分别为:pA=____________;pB=__________.
课堂训练
2.如图所示,开口向上竖直放置的内壁光滑气缸,其侧壁是绝热的,底部导热,内有两个质量均为m的密闭活塞,活塞A导热,活塞B绝热,将缸内理想气体分成Ⅰ、Ⅱ两部分.初状态整个装置静止不动且处于平衡状态,Ⅰ、Ⅱ两部分气体的高度均为L,温度为T.设外界大气压强为P保持不变,活塞横截面积为S,且mg=PS,环境温度保持不变.求:在活塞A上逐渐添加铁砂,当铁砂质量等于2m时,两活塞在某位置重新处于平衡,求:活塞B和A下降的高度分别多少?
,
解:对I气体,初状态p1=p0+=2p0,末状态p′1=p0+=4p0
2P0LS=4P0L1S 解得:L1=L /2
设压缩后气体柱长度为L1
对气体Ⅱ,初状态P2=3P0 ,末状态P2 ′=5P0
设压缩后气体柱长度为L2
3P0LS=5P0L2S 解得:L2=3L /5
B活塞下移距离△L2=L-3L /5=2L /5
A活塞下移距离△L1=(L-L /2)+△L2=9L /10
3:一个足球的容积是2.5L。用打气筒给这个足球打气,每打一次都把体积为125mL、压强与大气压强相同的气体打进球内。如果在打气前足球就已经是球形并且里面的压强与大气压强相同。打了20次后,足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
解:研究对象:打完20次气后足球内的气体,假设气体的温度和球的体积均不发生变化,设大气压强为p0,则
初态:压强p1=p0, V1=2.5+0.125×20=5L
末态:压强p2=? 体积为打气后V2=2.5L,
据玻意耳定律有:p1V1=p2V2 得:
p0×5=p2×2.5解得:p2=2p0
8.1 气体的等温变化(2)
专题:封闭气体压强的计算
学习目标:
掌握封闭气体压强的计算方法。
思考:
1:压强的定义及定义式是怎样的?
2:气体的压强是如何产生的?
3:封闭在容器中的气体的压强如何计算?
一:气体压强产生的原因:
大量分子无规则运动,频繁与器壁碰撞,宏观上对器壁产生了持续的压力。单位面积所受压力,叫压强。
一个空气分子,每秒钟与其它分子碰撞达65亿次之多。
容器中各处的压强相等
1. 理论依据
(1)液体压强的计算公式 p = ?gh。
(2)液面与外界大气相接触,则液面下h处的压强为 p = p0 + ?gh
(3)连通器原理:在连通器中,同一种液体(中间液体不间断)的同一水平面上的压强是相等的。
二、平衡态下液体封闭气体压强的计算
(1)连通器原理:根据同种液体在同一水平液面处压强相等,在连通器内灵活选取等压面.由两侧压强相等列方程求解压强.
例如图中,同一液面C、D处压强相等pA=p0+ph.
(2)参考液片法:选取假想的液体薄片(自身重力不计)为研究对象,分析液片两侧受力情况,建立平衡方程消去面积,得到液片两侧压强相等,进而求得气体压强.
例如,图中粗细均匀的U形管中封闭了一定质量的气体A,在其最低处取一液片B,由其两侧受力平衡可知
(pA+ph0)S=(p0+ph+ph0)S.即pA=p0+ph.
2.计算方法
(3)受力平衡法:选与封闭气体接触的液柱为研究对象进行受力分析,由F合=0列式求气体压强.
①
下列各图装置均处于静止状态。设大气压强为P0,用水银(或活塞)封闭一定量的气体在玻璃管(或气缸)中,求封闭气体的压强P
例1:
P =P0
P =P0+ρgh
P =P0- ρgh
h是水银柱在竖直方向的高度
连通器原理:同种液体在同一高度压强相等
P =P0+ρgh
P =P0- ρgh
P =P0- ρgh
练1:计算图2中各种情况下,被封闭气体的压强。(标准大气压强p0=76cmHg,图中液体为水银)
76cmHg
51cmHg
63.5cmHg
51cmHg
101cmHg
气体对面的压力与面垂直: F=PS
PS = P0S+mg
S′
PS =mg +P0S'cosθ
PS = mg+P0S
三、平衡态下固体密闭气体压强的计算
以活塞为研究对象
以气缸为研究对象
mg+PS = P0S
Mg+PS = P0S
练2:三个长方体容器中被光滑的活塞封闭一定质量的气体。如图3所示,M为重物质量,F是外力,p0为大气压,S为活塞面积,G为活塞重,则压强各为:
四、非平衡态下固体,液体闭气体压强的计算
当封闭气体的所在的系统处于力学非平衡状态时,欲求封闭气体压强,首先要选择 恰当的对象(如与气体相关的液体、活塞等)并对其进行正确的受力分析(特别注意分析内外的压力)然后应用牛顿第二定律列方程求解。
解得:P =P0+ρ(g-a)h
解:对液体柱,由牛顿第二定律得
P0S+mg-PS =ma
m=?hs
练3:如下图甲所示,气缸质量为m1,活塞质量为m2,不计缸内气体的质量及一切摩擦,当用一水平外力F拉活塞时,活塞和气缸最终以共同的加速度运动.求此时缸内气体的压强.(已知大气压为p0,活塞横截面积为S)
解:以气缸整体为研究对象,F=(m1+m2)a
以m2为研究对象,如图乙:F-P0S+PS=m2a
类型
1、液体密封气体
2、容器密封气体
3、气缸密封气体
课堂小结:
思路方法步骤
1、定对象
2、分析力
3、用规律
整体
部分
缸体
活塞
密封气体
静态∑F外=0
动态∑F外=ma
1.已知大气压强为p0,如图所示,竖直的U形管内A、B两部分被水银柱密封着,则两部分气体的压强分别为:pA=____________;pB=__________.
课堂训练
2.如图所示,开口向上竖直放置的内壁光滑气缸,其侧壁是绝热的,底部导热,内有两个质量均为m的密闭活塞,活塞A导热,活塞B绝热,将缸内理想气体分成Ⅰ、Ⅱ两部分.初状态整个装置静止不动且处于平衡状态,Ⅰ、Ⅱ两部分气体的高度均为L,温度为T.设外界大气压强为P保持不变,活塞横截面积为S,且mg=PS,环境温度保持不变.求:在活塞A上逐渐添加铁砂,当铁砂质量等于2m时,两活塞在某位置重新处于平衡,求:活塞B和A下降的高度分别多少?
,
解:对I气体,初状态p1=p0+=2p0,末状态p′1=p0+=4p0
2P0LS=4P0L1S 解得:L1=L /2
设压缩后气体柱长度为L1
对气体Ⅱ,初状态P2=3P0 ,末状态P2 ′=5P0
设压缩后气体柱长度为L2
3P0LS=5P0L2S 解得:L2=3L /5
B活塞下移距离△L2=L-3L /5=2L /5
A活塞下移距离△L1=(L-L /2)+△L2=9L /10
3:一个足球的容积是2.5L。用打气筒给这个足球打气,每打一次都把体积为125mL、压强与大气压强相同的气体打进球内。如果在打气前足球就已经是球形并且里面的压强与大气压强相同。打了20次后,足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
解:研究对象:打完20次气后足球内的气体,假设气体的温度和球的体积均不发生变化,设大气压强为p0,则
初态:压强p1=p0, V1=2.5+0.125×20=5L
末态:压强p2=? 体积为打气后V2=2.5L,
据玻意耳定律有:p1V1=p2V2 得:
p0×5=p2×2.5解得:p2=2p0
