2020湘教版八下数学1.3直角三角形全等的判定教学课件(20张)
文档属性
| 名称 | 2020湘教版八下数学1.3直角三角形全等的判定教学课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 1021.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-11 12:20:56 | ||
图片预览







文档简介
课件20张PPT。1.3 直角三角形全等的判定1.经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
2.掌握直角三角形全等的条件,并能运用其解决一些实际
问题.
3.在探索直角三角形全等条件及其运用的过程中,能够进
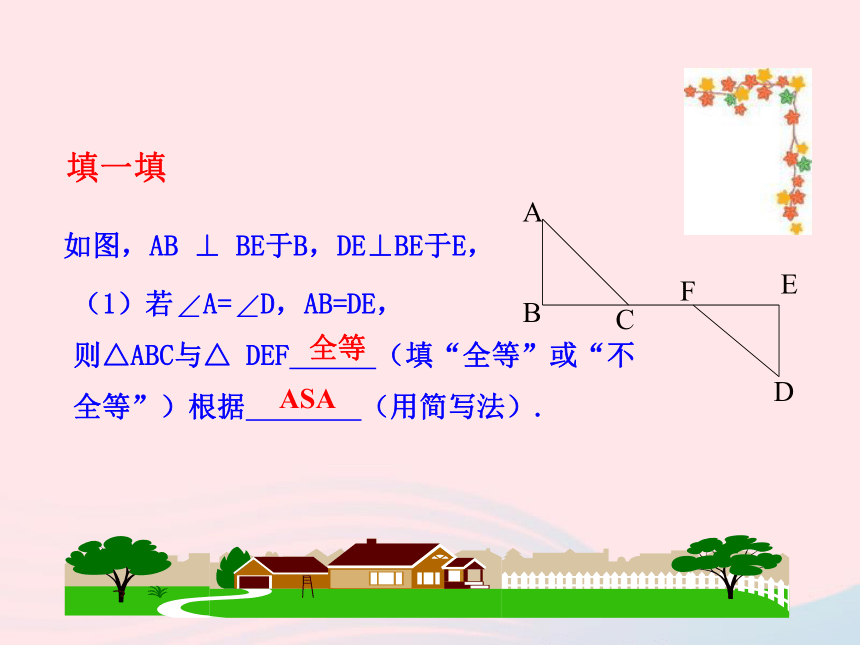
行有条理的思考并进行简单的推理.我们已经学过判定全等三角形的方法有哪些?1、边边边(SSS)3、角边角(ASA)4、角角边(AAS)2、边角边(SAS)如图,AB ⊥ BE于B,DE⊥BE于E,(1)若 A= D,AB=DE,
则△ABC与△ DEF (填“全等”或“不全等”)根据 (用简写法).全等ASA填一填(2)若 A= D,BC=EF,则△ABC与△DEF (填
“全等”或“不全等”)根据 (用简写法).AAS全等(3)若AB=DE,BC=EF,则△ABC与△DEF (填“全
等”或“不全等”)根据 (用简写法).全等SAS(4)若AB=DE,BC=EF,AC=DF,则
△ABC与△DEF (填“全等”或
“不全等”)根据_____(用简写法).
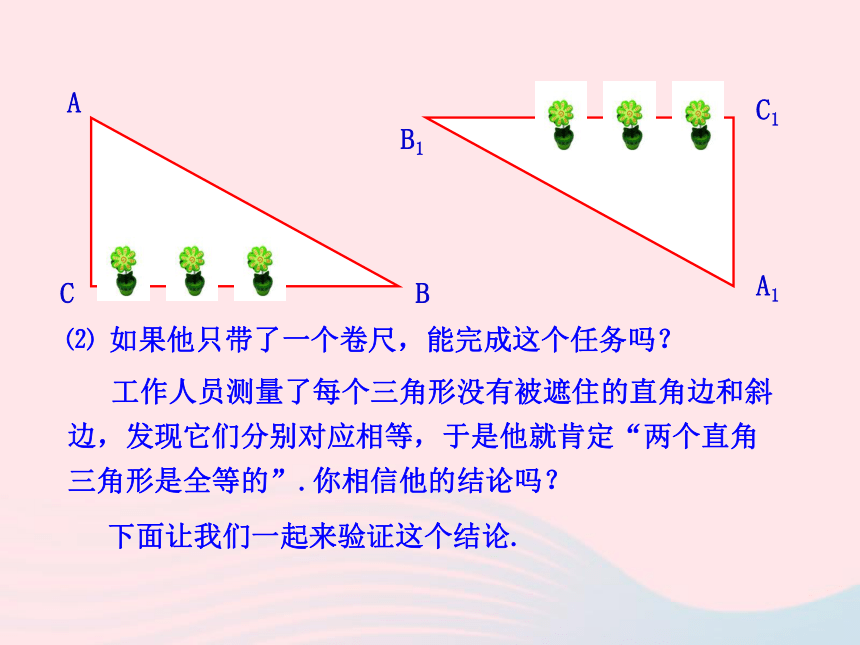
全等SSS 如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(1)你能帮他想个办法吗?方法一:测量斜边和一个对应的锐角. (AAS)方法二:测量没遮住的一条直角边和一个对应的锐
角.(ASA)或(AAS)⑵ 如果他只带了一个卷尺,能完成这个任务吗? 工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?下面让我们一起来验证这个结论. 任意画一个Rt△ACB ,使∠C﹦90°,再画一个Rt△A′C′B′使∠C﹦∠C′,B′C′﹦BC,A′B′﹦AB,
(1)你能试着画出来吗?与小组交流一下.(2)把画好的Rt△A′C′B′放到Rt△ACB上,它们全等吗?你能发现什么规律? 合作交流⑴ 作∠MC'N=90°;⑵ 在射线C'M上截取线段
C'B'=CB;⑶ 以B'为圆心,BA为半径画弧,交射线C'N于点A';⑷连接A'B'.C' 斜边和一条直角边分别相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”.定理【例】如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?【例题】【解析】在Rt△ABC和Rt△DEF中,∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°.则1.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.【跟踪训练】【证明】在Rt△ABF和Rt△CDE中,
∵AE=CF,
∴AF=CE.
又∵AB=CD,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.ABCDEF 2. 如图,两根长度为12 m的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由. BD=CD.
∵∠ADB=∠ADC=90°,
AB=AC,
AD=AD,∴Rt△ABD≌Rt△ACD(HL),
∴ BD=CD.【解析】1.(温州·中考)如图,AC,BD是矩形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有( )
A.1个 B.2个 C.3个 D.4个【解析】选D.在矩形ABCD中,△CDA、△BAD、△DBC都和△ABC全等,又∠ABC=∠DCE=90°,DE∥AC,所以∠DEC=∠ACB;又AB=DC,所以△DCE也和△ABC全等.2. 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?在Rt△ACB和Rt△ADB中,则∴ Rt△ACB≌Rt△ADB (HL).∴BC=BD
(全等三角形对应边相等).【解析】通过本课时的学习,需要我们掌握: 直角三角形是特殊的三角形,所以不仅有一般三角形
判定全等的方法: SSS、SAS、ASA、AAS,还有直角三角形
特殊的判定方法:HL. 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么.
——毕达哥拉斯
2.掌握直角三角形全等的条件,并能运用其解决一些实际
问题.
3.在探索直角三角形全等条件及其运用的过程中,能够进
行有条理的思考并进行简单的推理.我们已经学过判定全等三角形的方法有哪些?1、边边边(SSS)3、角边角(ASA)4、角角边(AAS)2、边角边(SAS)如图,AB ⊥ BE于B,DE⊥BE于E,(1)若 A= D,AB=DE,
则△ABC与△ DEF (填“全等”或“不全等”)根据 (用简写法).全等ASA填一填(2)若 A= D,BC=EF,则△ABC与△DEF (填
“全等”或“不全等”)根据 (用简写法).AAS全等(3)若AB=DE,BC=EF,则△ABC与△DEF (填“全
等”或“不全等”)根据 (用简写法).全等SAS(4)若AB=DE,BC=EF,AC=DF,则
△ABC与△DEF (填“全等”或
“不全等”)根据_____(用简写法).
全等SSS 如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(1)你能帮他想个办法吗?方法一:测量斜边和一个对应的锐角. (AAS)方法二:测量没遮住的一条直角边和一个对应的锐
角.(ASA)或(AAS)⑵ 如果他只带了一个卷尺,能完成这个任务吗? 工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?下面让我们一起来验证这个结论. 任意画一个Rt△ACB ,使∠C﹦90°,再画一个Rt△A′C′B′使∠C﹦∠C′,B′C′﹦BC,A′B′﹦AB,
(1)你能试着画出来吗?与小组交流一下.(2)把画好的Rt△A′C′B′放到Rt△ACB上,它们全等吗?你能发现什么规律? 合作交流⑴ 作∠MC'N=90°;⑵ 在射线C'M上截取线段
C'B'=CB;⑶ 以B'为圆心,BA为半径画弧,交射线C'N于点A';⑷连接A'B'.C' 斜边和一条直角边分别相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”.定理【例】如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?【例题】【解析】在Rt△ABC和Rt△DEF中,∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°.则1.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.【跟踪训练】【证明】在Rt△ABF和Rt△CDE中,
∵AE=CF,
∴AF=CE.
又∵AB=CD,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.ABCDEF 2. 如图,两根长度为12 m的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由. BD=CD.
∵∠ADB=∠ADC=90°,
AB=AC,
AD=AD,∴Rt△ABD≌Rt△ACD(HL),
∴ BD=CD.【解析】1.(温州·中考)如图,AC,BD是矩形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有( )
A.1个 B.2个 C.3个 D.4个【解析】选D.在矩形ABCD中,△CDA、△BAD、△DBC都和△ABC全等,又∠ABC=∠DCE=90°,DE∥AC,所以∠DEC=∠ACB;又AB=DC,所以△DCE也和△ABC全等.2. 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?在Rt△ACB和Rt△ADB中,则∴ Rt△ACB≌Rt△ADB (HL).∴BC=BD
(全等三角形对应边相等).【解析】通过本课时的学习,需要我们掌握: 直角三角形是特殊的三角形,所以不仅有一般三角形
判定全等的方法: SSS、SAS、ASA、AAS,还有直角三角形
特殊的判定方法:HL. 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么.
——毕达哥拉斯
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
