2020湘教版八下数学2.2.2平行四边形的判定第1课时教学课件(29张)
文档属性
| 名称 | 2020湘教版八下数学2.2.2平行四边形的判定第1课时教学课件(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 00:00:00 | ||
图片预览




文档简介
课件29张PPT。2.2.2 平行四边形的判定
第1课时 1.使学生感受平行四边形的判定方法1和2的形成过程,体会性质与判定的区别与联系.
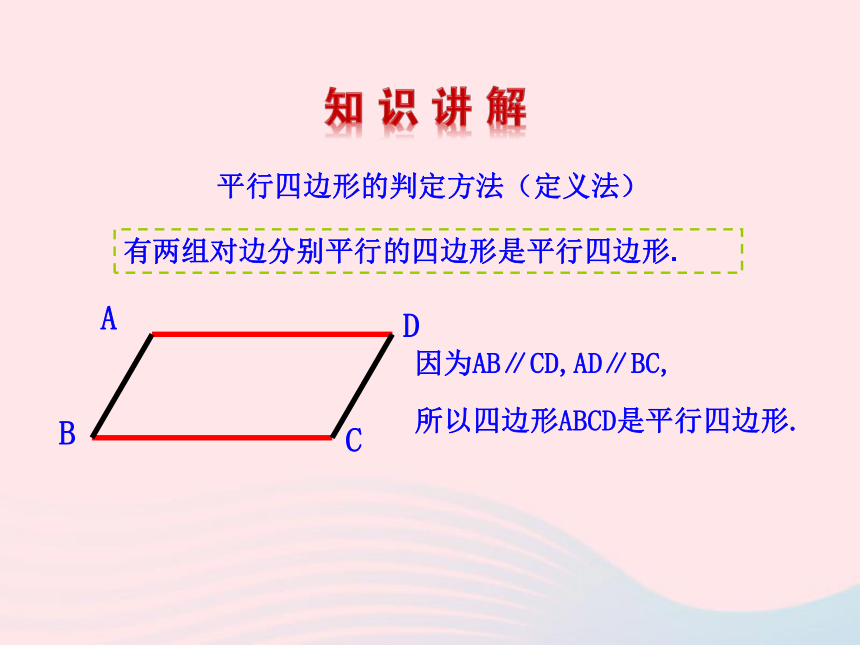
2.能运用平行四边形的判定方法和性质解决简单的推导问题,提高分析问题和解决问题的能力.边对角线角 平行四边形的对角线互相平分定义:两组对边分别平行的四边形是平行四边形.平行四边形的性质有两组对边分别平行的四边形是平行四边形.平行四边形的判定方法(定义法)因为AB∥CD,AD∥BC,所以四边形ABCD是平行四边形.探究1 对角线互相平分的四边形是平行四边形
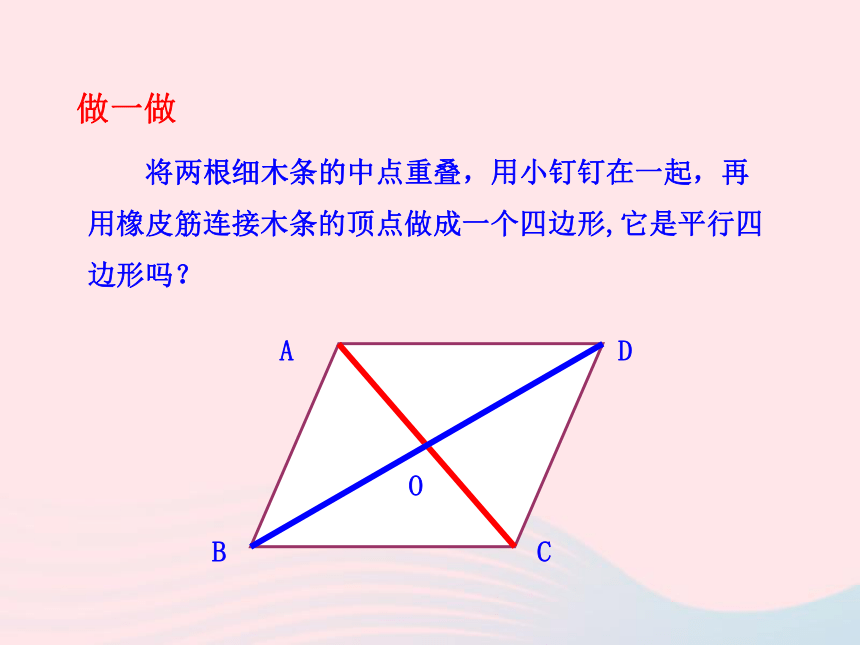
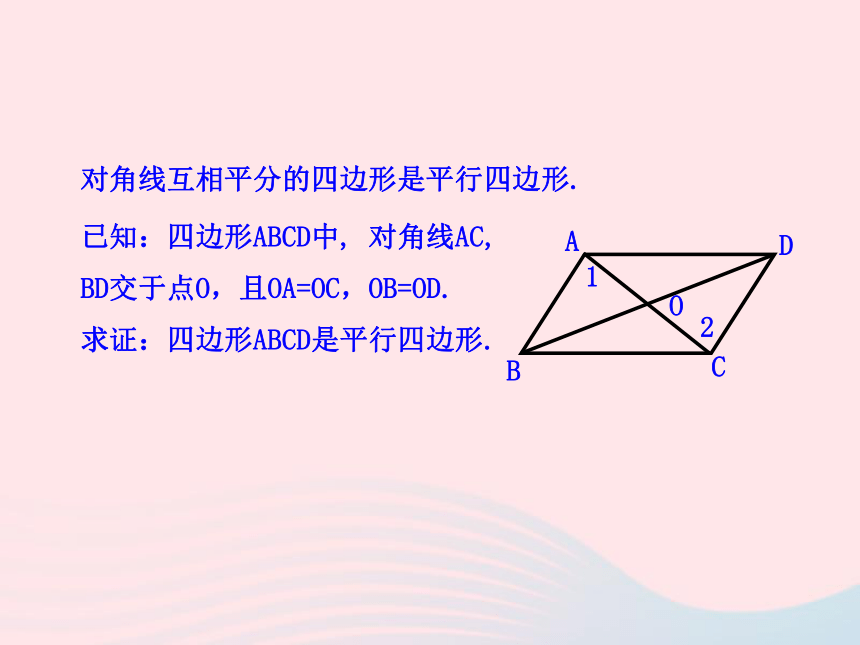
探究2 两组对角分别相等的四边形是平行四边形作业猜一猜 将两根细木条的中点重叠,用小钉钉在一起,再用橡皮筋连接木条的顶点做成一个四边形,它是平行四边形吗?做一做对角线互相平分的四边形是平行四边形.已知:四边形ABCD中, 对角线AC,
BD交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.证明:因为OA=OC OD=OB(已知)
∠AOB=∠COD(对顶角)
所以△AOB≌△COD(SAS)
所以∠1 = ∠2
所以AB∥CD
同理 AD∥BC
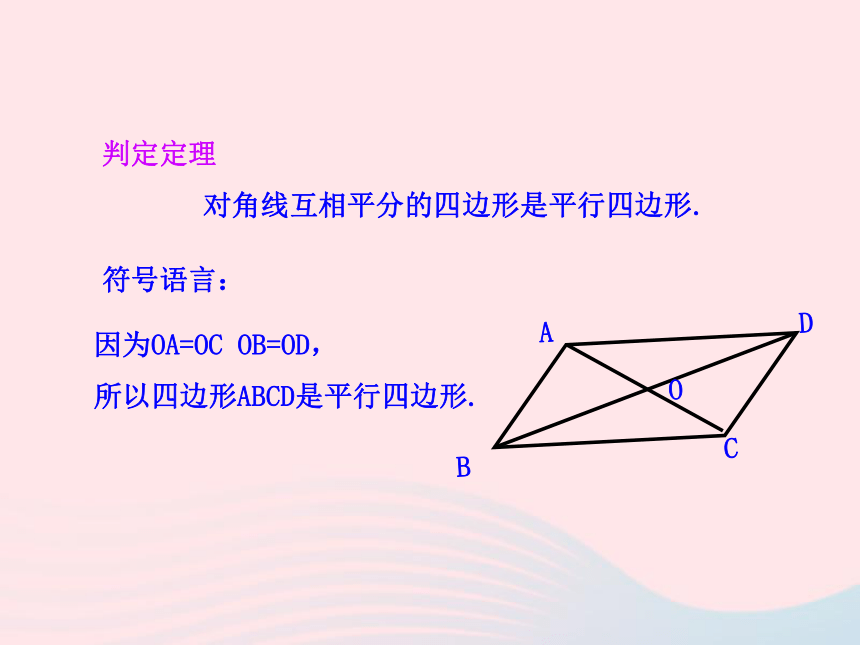
所以四边形ABCD是平行四边形判定定理
对角线互相平分的四边形是平行四边形.B符号语言:因为OA=OC OB=OD,
所以四边形ABCD是平行四边形.判断下列四边形是否是平行四边形?并说明理由.BADC110°110°⑴(2)ABCDO5㎝5㎝4㎝4㎝两组对边分别平行的四边形是
平行四边形两条对角线互相平分的四边形是
平行四边形70°【跟踪训练】70°解析(1)是平行四边形,理由:(2)是平行四边形,理由:例 在□ABCD中,点E,F是对角线AC上的两点,
且AE=CF,
求证:四边形BFDE是平行四边形.【例题】证明:连结BD,交AC于点O
因为四边形ABCD是平行四边形
所以OB=OD,OA=OC(平行四
边形的对角线互相平分)
因为AE=FC,
所以OE=OF,
所以四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形). 将一根木棒从AB平移到DC,AB与DC之间有怎样的位置关系、数量关系? 四边形ABCD是什么样的图形?【跟踪训练】AB猜测:一组对边平行且相等的四边形是平行四边形已知:AB∥CD,AB=CD.求证:四边形ABCD是平行四边形.判定定理 一组对边平行且相等的四边形是平行四边形.例 已知:平行四边形ABCD中,E,F分别是边AD,BC的中点. 求证:四边形EBFD是平行四边形.【例题】证明:因为四边形ABCD是平行四边形. 因为ED= AD, BF= BC, 所以四边形EBFD是平行四边形(一
组对边平行且相等的四边形是平
行四边形).所以AD BC, 所以ED BF, 思考:
1.你还有其他的证法吗?
2.如果把求证换成BE=FD,你会证吗?2.一组对边平行,一组对边相等的四边形是平行四边形吗?1.如图,四边形ABCD, ⑴若AB∥CD,______,则得到□ABCD; ⑵若AB=CD,______,则得到□ABCD. AB=CDAB∥CD【解析】不一定,如图所示的四边形就不是平行四边形【跟踪训练】3.已知:如图,在□ABCD中,BF=DE.
求证:四边形AFCE是平行四边形.
分析:由已知的平行四边形和BF=DE可知,CE=AF,则转化为利用一组对应边平行且相等来证明.【解析】2.已知:四边形ABCD中,AD∥BC,分别添上下列条件:
①AB∥CD;②AB=CD;③AD=BC;
④∠A=∠C;⑤∠B=∠C;
⑥∠A+∠D=∠B+∠C.
能使四边形ABCD为平行四边形的有( )
(A)①②③④ (B)①③④⑤
(C)①④⑤⑥ (D)①③④⑥
【解析】选D.添上①是平行四边形的定义,添上③是平行四边形的一个判定定理,由④能推出另两个对角相等,由⑥能推出另一组对边平行.【解析】答案:4.(滨州·中考)如图,平行四边形ABCD中,∠ABC=60°,E,F分别在CD,BC的延长线上,AE∥BD,EF⊥BC,DF=2,则EF的长为________.【解析】由题意易证,四边形ABDE是平行四边形,又四边形ABCD是平行四边形,所以CD=DE,又EF⊥CF,所以CE=4,易证∠CEF=30°,所以CF=2,所以
EF=
答案:5.(中山·中考)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连结DF.
(1)证明AC=EF;
(2)求证:四边形ADFE是平行四边形.【证明】(1)在Rt△ABC中,∠BAC=30°,
所以∠ABC=60°,
等边△ABE中,∠ABE=60°且AB=BE.
因为EF⊥AB,所以∠EFB=90°,
所以Rt△ABC≌Rt△EBF,
所以AC=EF.
(2)等边△ACD中,∠DAC=60°,AD=AC,
又因为∠BAC=30°,所以∠DAF=90°,
所以AD∥EF,
又因为AC=EF,所以AD=EF.
所以四边形ADFE是平行四边形. 本节课学习了平行四边形的判定方法:一组对边平行且相等平行四边形的定义的四边形是平行四边形对角线互相平分要求:1.会利用对角线关系和一组对边的关系判定一个四边形是不是平行四边形.
2.会综合运用平行四边形的判定定理和性质来解决问题.世上没有绝望的处境,只有对处境绝望的人.
第1课时 1.使学生感受平行四边形的判定方法1和2的形成过程,体会性质与判定的区别与联系.
2.能运用平行四边形的判定方法和性质解决简单的推导问题,提高分析问题和解决问题的能力.边对角线角 平行四边形的对角线互相平分定义:两组对边分别平行的四边形是平行四边形.平行四边形的性质有两组对边分别平行的四边形是平行四边形.平行四边形的判定方法(定义法)因为AB∥CD,AD∥BC,所以四边形ABCD是平行四边形.探究1 对角线互相平分的四边形是平行四边形
探究2 两组对角分别相等的四边形是平行四边形作业猜一猜 将两根细木条的中点重叠,用小钉钉在一起,再用橡皮筋连接木条的顶点做成一个四边形,它是平行四边形吗?做一做对角线互相平分的四边形是平行四边形.已知:四边形ABCD中, 对角线AC,
BD交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.证明:因为OA=OC OD=OB(已知)
∠AOB=∠COD(对顶角)
所以△AOB≌△COD(SAS)
所以∠1 = ∠2
所以AB∥CD
同理 AD∥BC
所以四边形ABCD是平行四边形判定定理
对角线互相平分的四边形是平行四边形.B符号语言:因为OA=OC OB=OD,
所以四边形ABCD是平行四边形.判断下列四边形是否是平行四边形?并说明理由.BADC110°110°⑴(2)ABCDO5㎝5㎝4㎝4㎝两组对边分别平行的四边形是
平行四边形两条对角线互相平分的四边形是
平行四边形70°【跟踪训练】70°解析(1)是平行四边形,理由:(2)是平行四边形,理由:例 在□ABCD中,点E,F是对角线AC上的两点,
且AE=CF,
求证:四边形BFDE是平行四边形.【例题】证明:连结BD,交AC于点O
因为四边形ABCD是平行四边形
所以OB=OD,OA=OC(平行四
边形的对角线互相平分)
因为AE=FC,
所以OE=OF,
所以四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形). 将一根木棒从AB平移到DC,AB与DC之间有怎样的位置关系、数量关系? 四边形ABCD是什么样的图形?【跟踪训练】AB猜测:一组对边平行且相等的四边形是平行四边形已知:AB∥CD,AB=CD.求证:四边形ABCD是平行四边形.判定定理 一组对边平行且相等的四边形是平行四边形.例 已知:平行四边形ABCD中,E,F分别是边AD,BC的中点. 求证:四边形EBFD是平行四边形.【例题】证明:因为四边形ABCD是平行四边形. 因为ED= AD, BF= BC, 所以四边形EBFD是平行四边形(一
组对边平行且相等的四边形是平
行四边形).所以AD BC, 所以ED BF, 思考:
1.你还有其他的证法吗?
2.如果把求证换成BE=FD,你会证吗?2.一组对边平行,一组对边相等的四边形是平行四边形吗?1.如图,四边形ABCD, ⑴若AB∥CD,______,则得到□ABCD; ⑵若AB=CD,______,则得到□ABCD. AB=CDAB∥CD【解析】不一定,如图所示的四边形就不是平行四边形【跟踪训练】3.已知:如图,在□ABCD中,BF=DE.
求证:四边形AFCE是平行四边形.
分析:由已知的平行四边形和BF=DE可知,CE=AF,则转化为利用一组对应边平行且相等来证明.【解析】2.已知:四边形ABCD中,AD∥BC,分别添上下列条件:
①AB∥CD;②AB=CD;③AD=BC;
④∠A=∠C;⑤∠B=∠C;
⑥∠A+∠D=∠B+∠C.
能使四边形ABCD为平行四边形的有( )
(A)①②③④ (B)①③④⑤
(C)①④⑤⑥ (D)①③④⑥
【解析】选D.添上①是平行四边形的定义,添上③是平行四边形的一个判定定理,由④能推出另两个对角相等,由⑥能推出另一组对边平行.【解析】答案:4.(滨州·中考)如图,平行四边形ABCD中,∠ABC=60°,E,F分别在CD,BC的延长线上,AE∥BD,EF⊥BC,DF=2,则EF的长为________.【解析】由题意易证,四边形ABDE是平行四边形,又四边形ABCD是平行四边形,所以CD=DE,又EF⊥CF,所以CE=4,易证∠CEF=30°,所以CF=2,所以
EF=
答案:5.(中山·中考)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连结DF.
(1)证明AC=EF;
(2)求证:四边形ADFE是平行四边形.【证明】(1)在Rt△ABC中,∠BAC=30°,
所以∠ABC=60°,
等边△ABE中,∠ABE=60°且AB=BE.
因为EF⊥AB,所以∠EFB=90°,
所以Rt△ABC≌Rt△EBF,
所以AC=EF.
(2)等边△ACD中,∠DAC=60°,AD=AC,
又因为∠BAC=30°,所以∠DAF=90°,
所以AD∥EF,
又因为AC=EF,所以AD=EF.
所以四边形ADFE是平行四边形. 本节课学习了平行四边形的判定方法:一组对边平行且相等平行四边形的定义的四边形是平行四边形对角线互相平分要求:1.会利用对角线关系和一组对边的关系判定一个四边形是不是平行四边形.
2.会综合运用平行四边形的判定定理和性质来解决问题.世上没有绝望的处境,只有对处境绝望的人.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
