2020北师版九上数学2.2用配方法求解一元二次方程习题课件(18张PPT)
文档属性
| 名称 | 2020北师版九上数学2.2用配方法求解一元二次方程习题课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 00:00:00 | ||
图片预览






文档简介
课件18张PPT。2 用配方法求解一元二次方程
第1课时1.完全平方式的定义:
形如__________的式子称为完全平方式.a2±2ab+b22.配方:
在下列式子中,填上适当的数,使等式成立.
x2+6x+__=(x+3)2;
x2-12x+___=(x-__)2;
x2+10x+___=(x+__)2.
(1)观察以上各式,可知方程左边填写的常数项是一次项系数
___________,右边填写的是一次项系数的_____________.
(2)二次项系数为1的完全平方式,其常数项等于一次项系数
___________.9366255一半的平方一半的绝对值一半的平方3.配方法的定义:
通过配成___________的方法得到一元二次方程的根,这种解
一元二次方程的方法称为配方法.完全平方式【思维诊断】(打“√”或“×”)
1.方程x2-1=0的解是x=1. ( )
2.方程(x+m)2=n(n≥0)的解是x=-m± . ( )
3.所有的一元二次方程都有实数解. ( )
4.方程(x-2)2-9=0的解是x=5. ( )×√××知识点 用配方法解二次项系数为1的一元二次方程
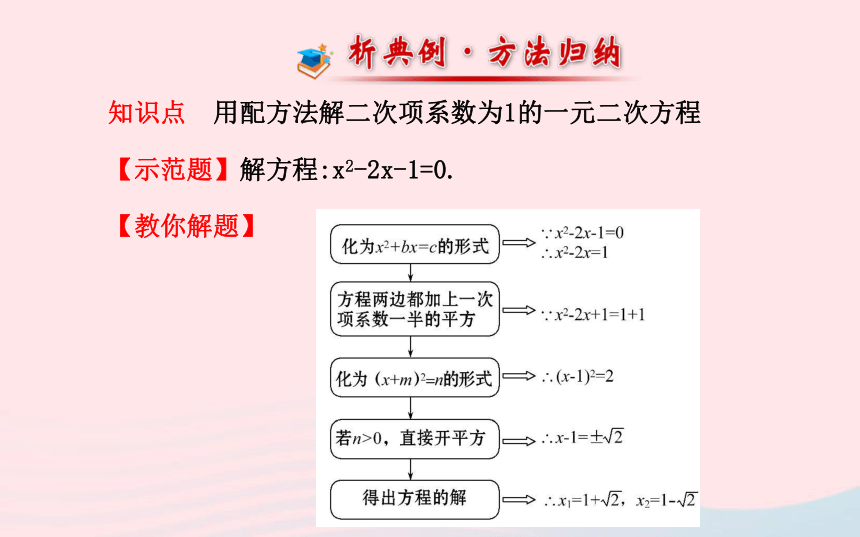
【示范题】解方程:x2-2x-1=0.
【教你解题】【想一想】
把一元二次方程配成(x+m)2=n的形式后,如果n<0,那么方程解的情况是怎样的?
提示:因为负数没有平方根,所以当n<0时,方程没有实数根.【微点拨】
1.形如x2=n(n≥0),(x+m)2=n(n≥0)的方程都能用直接开平方法求解.
2.把一元二次方程配成x2=n(n≥0),(x+m)2=n(n≥0)的形式后,就能用直接开平方法求解.
3.配方添项时方程两边需同时加上一次项系数一半的平方.
4.配方后方程的右边是非负数时,才能用直接开平方法求解.
5.开平方时方程的两边要同时开平方.【方法一点通】
用配方法解方程的“三个步骤”
1.化:把原方程化为x2+bx=c的形式.
2.配:在方程的左、右两边同时加上一次项系数一半的平方,配成(x+m)2=n的形式.
3.求:若n≥0,两边开平方,求出方程的根为x=-m± ;
若n<0,则此方程没有实数根.2 用配方法求解一元二次方程
第2课时1.用配方法解方程3x2-9x+1=0:
解:二次项系数化为1,得______________=0,
移项,得_____=________,
配方,得_______________=_______________,
整理,得___________=________,
两边开平方,得______=±____,所以x1=________,x2=_______.x2-3x2.用配方法解二次项系数不为1的一元二次方程的一般步骤:
(1)化:化___________为1.
(2)移项:使方程左边为_______________,右边为_______.
(3)配方:方程两边同时加上_____________________,使原方程
变为________的形式.
(4)开方:若方程右边为负数,则方程没有实数根,若方程右边为
_______,就可左右两边开平方得x+m=_____.
(5)求解:方程的解为x=_________.二次项系数二次项和一次项常数项一次项系数一半的平方(x+m)2=n非负数【思维诊断】(打“√”或“×”)
1.2t2-7t-4=0可化为 ( )
2.一元二次方程4x2-x+ =0的根为x1=x2=- . ( )
3.所有的一元二次方程都能用配方法求解. ( )
4.配方后方程的右边一定会大于0. ( )××√×知识点 用配方法解二次项系数不为1的一元二次方程
【示范题】解方程:5x2-x-2=0.
【思路点拨】系数化为1→配方→确定方程的解.【自主解答】二次项系数化为1,得
移项,得
配方,得
【想一想】
将方程2x2+5x+6=0和将代数式2x2+5x+6进行配方有何区别?
提示:将方程2x2+5x+6=0进行配方时,一般先将方程两边都除以2,再进行配方.而将代数式2x2+5x+6进行配方时,先提取二次项系数2,再进行配方.【备选例题】若x为任意实数,求-2x2+4x+7的最大值.
【解析】-2x2+4x+7=-2(x2-2x)+7
=-2(x2-2x+1)+2+7=-2(x-1)2+9,
∵-2(x-1)2≤0,∴-2(x-1)2+9≤9,
因此-2x2+4x+7的最大值为9.【方法一点通】
用配方法解方程应注意的“三个方面”
1.不漏除:二次项系数化为1时,方程中各项都要除以二次项系数.
2.式恒等:配方时始终要保证等式的成立.
3.不错号:不要弄错完全平方式中的符号.
第1课时1.完全平方式的定义:
形如__________的式子称为完全平方式.a2±2ab+b22.配方:
在下列式子中,填上适当的数,使等式成立.
x2+6x+__=(x+3)2;
x2-12x+___=(x-__)2;
x2+10x+___=(x+__)2.
(1)观察以上各式,可知方程左边填写的常数项是一次项系数
___________,右边填写的是一次项系数的_____________.
(2)二次项系数为1的完全平方式,其常数项等于一次项系数
___________.9366255一半的平方一半的绝对值一半的平方3.配方法的定义:
通过配成___________的方法得到一元二次方程的根,这种解
一元二次方程的方法称为配方法.完全平方式【思维诊断】(打“√”或“×”)
1.方程x2-1=0的解是x=1. ( )
2.方程(x+m)2=n(n≥0)的解是x=-m± . ( )
3.所有的一元二次方程都有实数解. ( )
4.方程(x-2)2-9=0的解是x=5. ( )×√××知识点 用配方法解二次项系数为1的一元二次方程
【示范题】解方程:x2-2x-1=0.
【教你解题】【想一想】
把一元二次方程配成(x+m)2=n的形式后,如果n<0,那么方程解的情况是怎样的?
提示:因为负数没有平方根,所以当n<0时,方程没有实数根.【微点拨】
1.形如x2=n(n≥0),(x+m)2=n(n≥0)的方程都能用直接开平方法求解.
2.把一元二次方程配成x2=n(n≥0),(x+m)2=n(n≥0)的形式后,就能用直接开平方法求解.
3.配方添项时方程两边需同时加上一次项系数一半的平方.
4.配方后方程的右边是非负数时,才能用直接开平方法求解.
5.开平方时方程的两边要同时开平方.【方法一点通】
用配方法解方程的“三个步骤”
1.化:把原方程化为x2+bx=c的形式.
2.配:在方程的左、右两边同时加上一次项系数一半的平方,配成(x+m)2=n的形式.
3.求:若n≥0,两边开平方,求出方程的根为x=-m± ;
若n<0,则此方程没有实数根.2 用配方法求解一元二次方程
第2课时1.用配方法解方程3x2-9x+1=0:
解:二次项系数化为1,得______________=0,
移项,得_____=________,
配方,得_______________=_______________,
整理,得___________=________,
两边开平方,得______=±____,所以x1=________,x2=_______.x2-3x2.用配方法解二次项系数不为1的一元二次方程的一般步骤:
(1)化:化___________为1.
(2)移项:使方程左边为_______________,右边为_______.
(3)配方:方程两边同时加上_____________________,使原方程
变为________的形式.
(4)开方:若方程右边为负数,则方程没有实数根,若方程右边为
_______,就可左右两边开平方得x+m=_____.
(5)求解:方程的解为x=_________.二次项系数二次项和一次项常数项一次项系数一半的平方(x+m)2=n非负数【思维诊断】(打“√”或“×”)
1.2t2-7t-4=0可化为 ( )
2.一元二次方程4x2-x+ =0的根为x1=x2=- . ( )
3.所有的一元二次方程都能用配方法求解. ( )
4.配方后方程的右边一定会大于0. ( )××√×知识点 用配方法解二次项系数不为1的一元二次方程
【示范题】解方程:5x2-x-2=0.
【思路点拨】系数化为1→配方→确定方程的解.【自主解答】二次项系数化为1,得
移项,得
配方,得
【想一想】
将方程2x2+5x+6=0和将代数式2x2+5x+6进行配方有何区别?
提示:将方程2x2+5x+6=0进行配方时,一般先将方程两边都除以2,再进行配方.而将代数式2x2+5x+6进行配方时,先提取二次项系数2,再进行配方.【备选例题】若x为任意实数,求-2x2+4x+7的最大值.
【解析】-2x2+4x+7=-2(x2-2x)+7
=-2(x2-2x+1)+2+7=-2(x-1)2+9,
∵-2(x-1)2≤0,∴-2(x-1)2+9≤9,
因此-2x2+4x+7的最大值为9.【方法一点通】
用配方法解方程应注意的“三个方面”
1.不漏除:二次项系数化为1时,方程中各项都要除以二次项系数.
2.式恒等:配方时始终要保证等式的成立.
3.不错号:不要弄错完全平方式中的符号.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
