2020北师大版九上数学2.6应用一元二次方程习题讲解课件(2课时 24张)
文档属性
| 名称 | 2020北师大版九上数学2.6应用一元二次方程习题讲解课件(2课时 24张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 16:42:58 | ||
图片预览







文档简介
课件24张PPT。6 应用一元二次方程
第1课时列一元二次方程解应用题的一般步骤:
①审:审清题意,找出_________;
②设:设出_______,用所设的_______表示其他未知量;
③列:列一元二次方程;
④解:解一元二次方程;
⑤验:检验所求的解是否符合题意,确定_______的值;
⑥答:作答.等量关系未知数未知数未知数【思维诊断】(打“√”或“×”)
1.所有的应用题都能通过列一元二次方程解决. ( )
2.实际问题中的等量关系只能有一个. ( )
3.列方程解决实际问题时,方程的解既要满足所列方程,还要符
合实际问题的具体题意. ( )
4.列方程解决实际问题时,方程的解只要不是负数,就符合实际
要求. ( )××√×知识点 利用一元二次方程解决几何问题
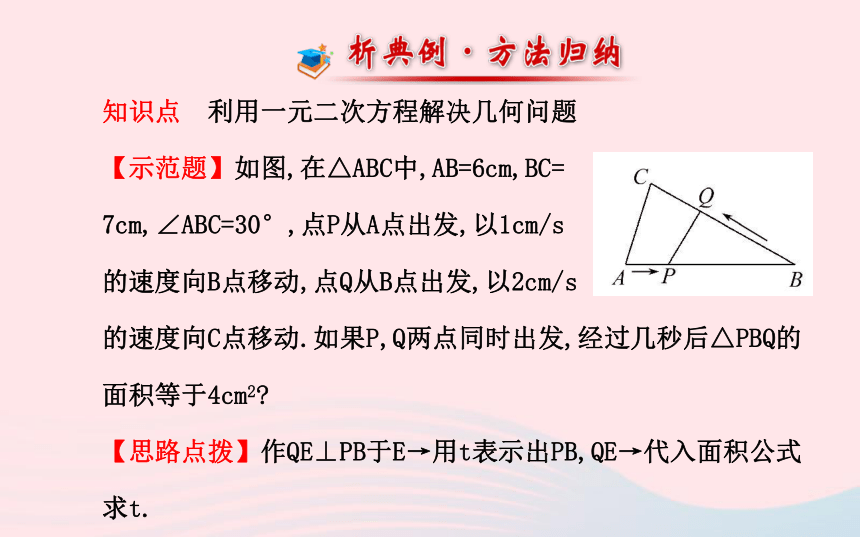
【示范题】如图,在△ABC中,AB=6cm,BC=
7cm,∠ABC=30°,点P从A点出发,以1cm/s
的速度向B点移动,点Q从B点出发,以2cm/s
的速度向C点移动.如果P,Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?
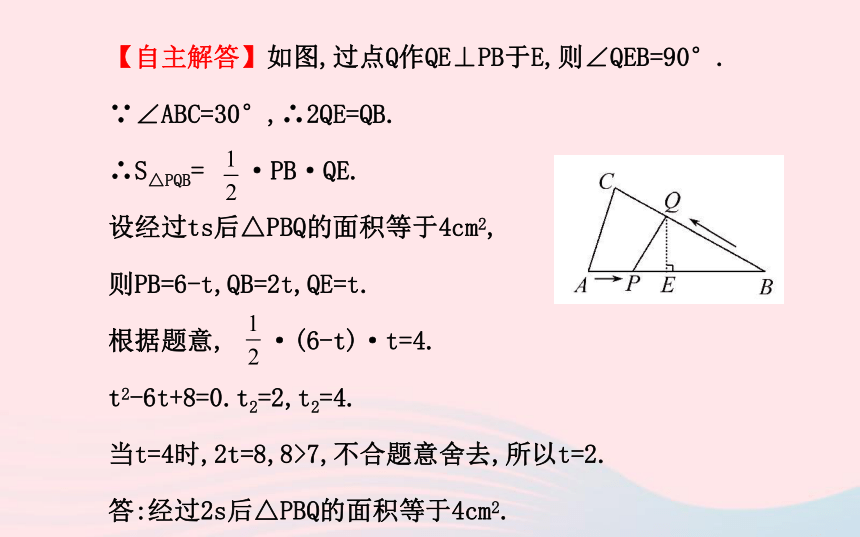
【思路点拨】作QE⊥PB于E→用t表示出PB,QE→代入面积公式求t.【自主解答】如图,过点Q作QE⊥PB于E,则∠QEB=90°.
∵∠ABC=30°,∴2QE=QB.
∴S△PQB= ·PB·QE.
设经过ts后△PBQ的面积等于4cm2,
则PB=6-t,QB=2t,QE=t.
根据题意, ·(6-t)·t=4.
t2-6t+8=0.t2=2,t2=4.
当t=4时,2t=8,8>7,不合题意舍去,所以t=2.
答:经过2s后△PBQ的面积等于4cm2.【想一想】
当△PBQ的面积等于4cm2时,△PBQ是什么形状的三角形?
提示:∵△PBQ的面积等于4cm2时t=2,
∴PB=6-t=6-2=4,QB=2t=4,∴QB=PB,
∴△PBQ是等腰三角形.【微点拨】
1.列一元二次方程解应用题时,要注意挖掘题目中隐含的等量关系.
2.方程的解既要满足所列方程,还要符合实际问题的具体题意.
3.题目中的等量关系可能不止一个,其中的一个等量关系用来列方程,另一些等量关系用来列代数式.【方法一点通】
几何问题中常见的等量关系
(1)当题目中有直角三角形时,常借助勾股定理建立一元二次方程.
(2)当题目中涉及图形面积(体积)时,常通过图形的面积(体积)公式建立方程.6 应用一元二次方程
第2课时1.利润问题中常用的等量关系
(1)单件利润=_________-单件成本.
(2)总利润=_________×销售件数=_______-总成本.
(3)利润=进价×利润率.单件售价单件利润总售价2.增长率方面的应用题
此类问题是在某个数据的基础上连续增长(降低)两次得到新的
数据,解这类问题需牢记公式_________或a(1-x)2=b,其中a表
示_____________的数据,x表示增长率或降低率,b表示后来得
到的数据,“+”表示_____,“-”表示_____.a(1+x)2=b增长(降低)前增长降低【思维诊断】(打“√”或“×”)
1.在商品的利润问题中只能直接设未知数.( )
2.增长率不能是负数,且不能大于1.( )
3.增长率和降低率均不能是负数.( )
4.10元一件的商品9折卖出,则该件商品的售价是19元.( ) ××√×知识点一 一元二次方程在利润问题中的应
【示范题1】小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件,如果一次性购买不超过10件,单价为80元;如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元,按此优惠条件,小丽一次性购买这种服装付了1200元,请问她购买了多少件这种服装?【教你解题】【想一想】
如果小丽再加50元钱,她可以多买几件服装?
提示:设小丽此时可购买y件服装,则有y[80-2(y-10)]=1250,
解得x1= x2=25,
1250÷25=50,符合题意,
所以她可以多买5件服装.【微点拨】增长率(或降低率)问题的规律
1.增长率问题:设基数为a,平均增长率为x,则一次增长后的值为a(1+x),两次增长后的值为a(1+x)2,依次类推,n次增长后的值为a(1+x)n.
2.降低率问题:设基数为a,平均降低率为x,则一次降低后的值为a(1-x),两次降低后的值为a(1-x)2,依次类推,n次降低后的值为a(1-x)n.【方法一点通】
解答商业利润问题的两点注意
1.理清利润、成本和其他费用之间的关系,然后用数学语言描述等量关系,再列方程,求出解后再进行实际意义的验证.
2.充分利用题目中的已知条件,挖掘隐含条件,找出数量关系.同时多方面考虑实际问题中取值的意义.知识点二 一元二次方程在经济中的应用——增长率问题
【示范题2】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10000元,第三天收到捐款12100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率.
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?【思路点拨】(1)利用等量关系:第一天收到捐款钱数×(1+增长率)2=第三天收到捐款钱数,设出未知数,列方程解答即可.
(2)第三天收到捐款钱数×(1+增长率)=第四天收到捐款钱数.【自主解答】(1)设捐款增长率为x,
则10000(1+x)2=12100,
解这个方程,得x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:捐款的增长率为10%.
(2)12100×(1+10%)=13310.
答:按照(1)中收到捐款的增长速度,第四天该单位能收到捐款13310元.【想一想】
增长率能大于1吗?
提示:增长率能大于1.【备选例题】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20kg,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?【解析】(1)设每千克核桃应降价x元.
根据题意,得
化简,得x2-10x+24=0,
解得x1=4,x2=6.
答:每千克核桃应降价4元或6元.
(2)由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.此时,售价为:60-6=54(元), ×100%=90%.
答:该店应按原售价的九折出售.【方法一点通】
平均增长率问题中常见的等量关系及注意事项
1.常见的等量关系:a(1±x)2=b,其中a表示原数据,x表示增长(降低)率,b表示后来得到的数据.
2.两点注意:(1)解此类问题一般用直接开平方法求解.
(2)增长(降低)率不能是负数,降低率要小于1.
第1课时列一元二次方程解应用题的一般步骤:
①审:审清题意,找出_________;
②设:设出_______,用所设的_______表示其他未知量;
③列:列一元二次方程;
④解:解一元二次方程;
⑤验:检验所求的解是否符合题意,确定_______的值;
⑥答:作答.等量关系未知数未知数未知数【思维诊断】(打“√”或“×”)
1.所有的应用题都能通过列一元二次方程解决. ( )
2.实际问题中的等量关系只能有一个. ( )
3.列方程解决实际问题时,方程的解既要满足所列方程,还要符
合实际问题的具体题意. ( )
4.列方程解决实际问题时,方程的解只要不是负数,就符合实际
要求. ( )××√×知识点 利用一元二次方程解决几何问题
【示范题】如图,在△ABC中,AB=6cm,BC=
7cm,∠ABC=30°,点P从A点出发,以1cm/s
的速度向B点移动,点Q从B点出发,以2cm/s
的速度向C点移动.如果P,Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?
【思路点拨】作QE⊥PB于E→用t表示出PB,QE→代入面积公式求t.【自主解答】如图,过点Q作QE⊥PB于E,则∠QEB=90°.
∵∠ABC=30°,∴2QE=QB.
∴S△PQB= ·PB·QE.
设经过ts后△PBQ的面积等于4cm2,
则PB=6-t,QB=2t,QE=t.
根据题意, ·(6-t)·t=4.
t2-6t+8=0.t2=2,t2=4.
当t=4时,2t=8,8>7,不合题意舍去,所以t=2.
答:经过2s后△PBQ的面积等于4cm2.【想一想】
当△PBQ的面积等于4cm2时,△PBQ是什么形状的三角形?
提示:∵△PBQ的面积等于4cm2时t=2,
∴PB=6-t=6-2=4,QB=2t=4,∴QB=PB,
∴△PBQ是等腰三角形.【微点拨】
1.列一元二次方程解应用题时,要注意挖掘题目中隐含的等量关系.
2.方程的解既要满足所列方程,还要符合实际问题的具体题意.
3.题目中的等量关系可能不止一个,其中的一个等量关系用来列方程,另一些等量关系用来列代数式.【方法一点通】
几何问题中常见的等量关系
(1)当题目中有直角三角形时,常借助勾股定理建立一元二次方程.
(2)当题目中涉及图形面积(体积)时,常通过图形的面积(体积)公式建立方程.6 应用一元二次方程
第2课时1.利润问题中常用的等量关系
(1)单件利润=_________-单件成本.
(2)总利润=_________×销售件数=_______-总成本.
(3)利润=进价×利润率.单件售价单件利润总售价2.增长率方面的应用题
此类问题是在某个数据的基础上连续增长(降低)两次得到新的
数据,解这类问题需牢记公式_________或a(1-x)2=b,其中a表
示_____________的数据,x表示增长率或降低率,b表示后来得
到的数据,“+”表示_____,“-”表示_____.a(1+x)2=b增长(降低)前增长降低【思维诊断】(打“√”或“×”)
1.在商品的利润问题中只能直接设未知数.( )
2.增长率不能是负数,且不能大于1.( )
3.增长率和降低率均不能是负数.( )
4.10元一件的商品9折卖出,则该件商品的售价是19元.( ) ××√×知识点一 一元二次方程在利润问题中的应
【示范题1】小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件,如果一次性购买不超过10件,单价为80元;如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元,按此优惠条件,小丽一次性购买这种服装付了1200元,请问她购买了多少件这种服装?【教你解题】【想一想】
如果小丽再加50元钱,她可以多买几件服装?
提示:设小丽此时可购买y件服装,则有y[80-2(y-10)]=1250,
解得x1= x2=25,
1250÷25=50,符合题意,
所以她可以多买5件服装.【微点拨】增长率(或降低率)问题的规律
1.增长率问题:设基数为a,平均增长率为x,则一次增长后的值为a(1+x),两次增长后的值为a(1+x)2,依次类推,n次增长后的值为a(1+x)n.
2.降低率问题:设基数为a,平均降低率为x,则一次降低后的值为a(1-x),两次降低后的值为a(1-x)2,依次类推,n次降低后的值为a(1-x)n.【方法一点通】
解答商业利润问题的两点注意
1.理清利润、成本和其他费用之间的关系,然后用数学语言描述等量关系,再列方程,求出解后再进行实际意义的验证.
2.充分利用题目中的已知条件,挖掘隐含条件,找出数量关系.同时多方面考虑实际问题中取值的意义.知识点二 一元二次方程在经济中的应用——增长率问题
【示范题2】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10000元,第三天收到捐款12100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率.
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?【思路点拨】(1)利用等量关系:第一天收到捐款钱数×(1+增长率)2=第三天收到捐款钱数,设出未知数,列方程解答即可.
(2)第三天收到捐款钱数×(1+增长率)=第四天收到捐款钱数.【自主解答】(1)设捐款增长率为x,
则10000(1+x)2=12100,
解这个方程,得x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:捐款的增长率为10%.
(2)12100×(1+10%)=13310.
答:按照(1)中收到捐款的增长速度,第四天该单位能收到捐款13310元.【想一想】
增长率能大于1吗?
提示:增长率能大于1.【备选例题】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20kg,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?【解析】(1)设每千克核桃应降价x元.
根据题意,得
化简,得x2-10x+24=0,
解得x1=4,x2=6.
答:每千克核桃应降价4元或6元.
(2)由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.此时,售价为:60-6=54(元), ×100%=90%.
答:该店应按原售价的九折出售.【方法一点通】
平均增长率问题中常见的等量关系及注意事项
1.常见的等量关系:a(1±x)2=b,其中a表示原数据,x表示增长(降低)率,b表示后来得到的数据.
2.两点注意:(1)解此类问题一般用直接开平方法求解.
(2)增长(降低)率不能是负数,降低率要小于1.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
