2020北师大版九上数学第二章一元二次方程阶段复习课件(40张)
文档属性
| 名称 | 2020北师大版九上数学第二章一元二次方程阶段复习课件(40张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 16:45:02 | ||
图片预览











文档简介
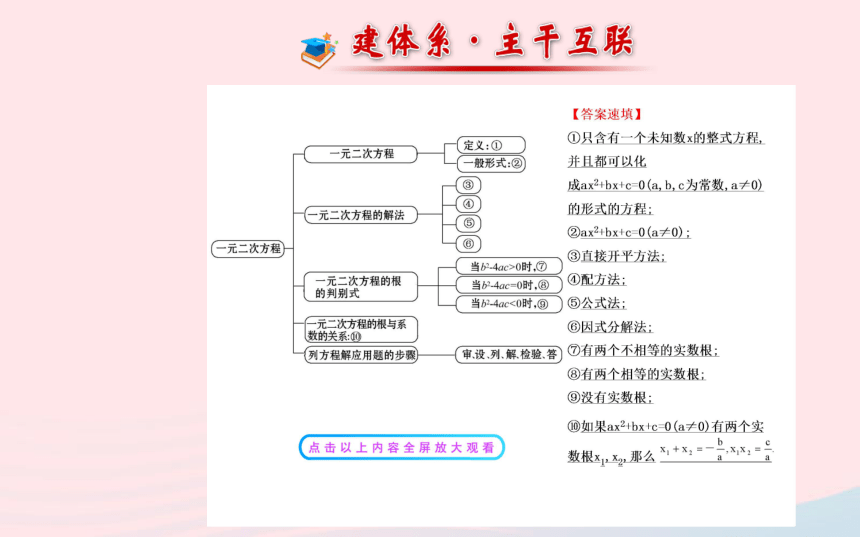
课件40张PPT。阶段复习课
第 二 章主题1 一元二次方程的相关概念与解法
【主题训练1】先化简,再求值:
(x-1)÷ 其中x为方程x2+3x+2=0的根.【自主解答】原式=
由x2+3x+2=0,得x1=-1,x2=-2.
当x=-1时,原式无意义,所以x=-1舍去,
当x=-2时,原式=1.【主题升华】
一元二次方程的有关概念
(1)一元二次方程满足的四个条件
(2)一元二次方程的项包括它前面的符号,一次项和常数项可以为0.
(3)根能使方程左右两边相等,已知一个根,可代入确定方程中的字母系数.1.一元二次方程x2-2x-3=0的解是
( )
A.x1=-1,x2=3 B.x1=1,x2=-3
C.x1=-1,x2=-3 D.x1=1,x2=3
【解析】选A.∵a=1,b=-2,c=-3,∴b2-4ac=16,
∴x= ∴x1=-1,x2=3.2.方程(2x+1)(3x-2)=0的解是 .
【解析】∵(2x+1)(3x-2)=0,
∴2x+1=0,3x-2=0,
答案: 3.已知x=-1是关于x的方程2x2+ax-a2=0的一个根,则a= .
【解析】根据题意得:2-a-a2=0,
解得a=-2或1.
答案:-2或14.解方程:x2-10x+9=0.
【解析】将方程x2-10x+9=0,
变形为:x2-10x=-9,
配方,x2-10x+25=-9+25,
整理,得(x-5)2=16,
解得,x1=1,x2=9.【一题多解】公式法:因为a=1,b=-10,c=9,
Δ=100-36=64>0,
由求根公式解得,x1=1,x2=9.
因式分解法:将方程x2-10x+9=0,
变形为:(x-1)(x-9)=0,
解得,x1=1,x2=9.【知识归纳】一元二次方程解法的理论依据及适用形式解读:配方法要先配方,再降次;公式法是判断b2-4ac>0后直接利用求根公式;分解因式法是把方程的一边化为两个一次因式的乘积,另一边为0.主题2 一元二次方程的根与b2-4ac的关系
【主题训练2】已知一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根.
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.【自主解答】(1)∵一元二次方程为x2-(2k+1)x+k2+k=0,
∴Δ=[-(2k+1)]2-4(k2+k)=1>0,
∴此方程有两个不相等的实数根.
(2)∵△ABC的两边AB,AC的长是这个方程的两个实数根,由(1)知,AB≠AC,△ABC的第三边BC的长为5,且△ABC是等腰三角形,
∴必然有AB=5或AC=5,即x=5是原方程的一个解.将x=5代入方程x2-(2k+1)x+k2+k=0,即25-5(2k+1)+k2+k=0,解得k=4或k=5.当k=4时,原方程为x2-9x +20=0,x1=5,x2=4,以5,5,4为边长能构成等腰三角形;
当k=5时,原方程为x2-11x +30=0,x1=5,x2=6,以5,5,6为边长能构成等腰三角形.
∴k的值为4或5.【主题升华】一元二次方程的根与b2-4ac的关系
(1)b2-4ac>0?方程有两个不相等的实数根.
(2)b2-4ac=0?方程有两个相等的实数根.
(3)b2-4ac<0?方程没有实数根.1.下列一元二次方程中,有两个不相等的实数根的方程是( )
A.x2-3x+1=0 B. x2+1=0
C.x2-2x+1=0 D.x2-2x+3=0【解析】选A.选项A中的b2-4ac>0,所以方程有两个不相等的实数根;选项B中的b2-4ac<0,所以方程没有实数根;选项C中的b2-4ac=0,所以方程有两个相等的实数根;选项D中的b2-4ac<0,所以方程没有实数根.2.已知关于x的一元二次方程x2+2x-a=0有两个相等的实数根,则a的值是 ( )
A.4 B.-4 C.1 D.-1
【解析】选D.∵关于x的一元二次方程x2+2x-a=0有两个相等的实数根,
∴Δ=b2-4ac=0,即22-4(-a)=0,解得:a=-1.3.已知关于x的方程x2-2(k-1)x+k2=0有两个实数根,求k的取值范围.
【解析】∵方程x2-2(k-1)x+k2=0有两个实数根,
∴b2-4ac≥0,即[-2(k-1)]2-4k2≥0,
∴4k2-8k+4-4k2≥0,解得k≤ .主题3 一元二次方程的根与系数的关系
【主题训练3】已知α,β是一元二次方程x2-5x-2=0的两个实数根,则α2+αβ+β2的值为 ( )
A.-1 B.9 C.23 D.27【自主解答】选D.∵α,β是一元二次方程x2-5x-2=0的两个实数根∴ ∴α2+αβ+β2=(α+β)2-αβ=52-(-2)=27.【主题升华】一元二次方程的根与系数的关系的三个应用
1.已知一个一元二次方程和它的一个根,不解方程,求另一个根或字母系数的值.
2.已知一个一元二次方程,不解方程,求关于它的两个根的某些代数式的值.
3.利用根与系数的关系求新的方程.1.设x1,x2是方程x2-3x-3=0的两个实数根,则
的值为 ( )
A.5 B.-5 C.1 D.-1【解题指南】本题涉及的三个知识点
(1)一元二次方程根与系数的关系.
(2)分式的运算.
(3)完全平方公式的变形.【解析】选B.由根与系数的关系可知
x1+x2=3,x1x2=-3,
2.已知x=-2是方程x2+mx-6=0的一个根,则方程的另一个根是 .
【解析】设方程另一个根为x1,根据题意得-2·x1=-6,所以x1=3.
答案:3【互动探究】本题中m的值是多少?
【解析】由题意求得方程的两个根分别是-2和3,
∴-2+3=-m,∴m=-1.3.若两个不等实数m,n满足条件:m2-2m-1=0,n2-2n-1=0,则m2+n2的值是 .
【解析】∵m2-2m-1=0,n2-2n-1=0,m≠n,∴m,n是x2-2x-1=0的两根,由根与系数关系得m+n=2,mn=-1,
∴m2+n2=(m+n)2-2mn=22-2×(-1)=6.
答案:64.关于x的一元二次方程x2-(m-3)x-m2=0.
(1)证明:方程总有两个不相等的实数根.
(2)设这个方程的两个实数根为x1,x2,且|x1|=|x2|-2,求m的值及方程的根.
【解析】(1)一元二次方程x2-(m-3)x-m2=0,
∵a=1,b=-(m-3)=3-m,c=-m2,
∴Δ=b2-4ac=(3-m)2-4×1×(-m2)=(3-m)2+4m2>0,
∴方程总有两个不相等的实数根.(2)由根与系数的关系得x1·x2= =-m2≤0,x1+x2=m-3,
∴x1,x2异号,
又|x1|=|x2|-2,即|x1|-|x2|=-2,
若x1>0,x2<0,上式化简得:x1+x2=-2,
∴m-3=-2,即m=1,
方程化为x2+2x-1=0,解得:x1=-1+ ,x2=-1- .
若x1<0,x2>0,上式化简得:-(x1+x2)=-2,
∴x1+x2=m-3=2,即m=5,
方程化为x2-2x-25=0,
解得:x1=1- ,x2=1+ .主题4 一元二次方程的应用
【主题训练4】 “4·20”雅安地震后,某商家为支援灾区人民,计划捐赠帐篷16800顶,该商家备有2辆大货车、8辆小货车运送,计划大货车比小货车每辆每次多运帐篷200顶,大、小货车每天均运送一次,两天恰好运完.
(1)求大、小货车原计划每辆每次各运送帐篷多少顶?(2)因地震导致路基受损,实际运送过程中,每辆大货车每次比
原计划少运200m顶,每辆小货车每次比原计划少运300顶.为了
尽快将帐篷运送到灾区,大货车每天比原计划多跑m次,小货车
每天比原计划多跑 m次,一天刚好运送了帐篷14400顶,求m的
值.【解析】(1)设小货车原计划每辆每次运送帐篷x顶,则大货车
原计划每辆每次运送帐篷(x+200)顶,根据题意,得2[8x+2(x+200)]=16800,解得x=800,
x+200=800+200=1000.
答:大、小货车原计划每辆每次分别运送帐篷1000顶,800顶.(2)根据题意,得
2(1000-200m)+8(800-300)(1+ m)=14400,化简为m2-23m+42=0,解得m1=2,m2=21.
∵1000-200m不能为负数,且 m为整数,
∴m=21不符合实际,舍去,
∴m的值为2.【主题升华】列一元二次方程解应用题的三点注意
1.审题:准确找出已知量与未知量之间的关系.
2.设元:分为直接设未知数和间接设未知数两种,对于直接设未知数列方程比较困难或列出的方程比较复杂时,要考虑采用间接设未知数.
3.检验:求出方程的解后,必须检验所求的解是否符合题目要求或客观实际,不符合的解需要舍去.1.某超市一月份的营业额为36万元,三月
份的营业额为48万元.设每月的平均增长率为x,则可列方程
为 ( )
A.48(1-x)2=36 B.48(1+x)2=36
C.36(1-x)2=48 D.36(1+x)2=48
【解析】选D.二月份的营业额为36(1+x),三月份的营业额为36(1+x)(1+x)=36(1+x)2,
即所列的方程为36(1+x)2=48.2.三角形的两边长分别为3和6,第三边是方程x2-6x+8=0的解,这个三角形的周长是 ( )
A.11 B.13 C.11或13 D.11和13
【解析】选B.解方程x2-6x+8=0,得x1=2,x2=4.∵2+3<6,∴第三边不能为2,当第三边为4时,周长为3+6+4=13.
第 二 章主题1 一元二次方程的相关概念与解法
【主题训练1】先化简,再求值:
(x-1)÷ 其中x为方程x2+3x+2=0的根.【自主解答】原式=
由x2+3x+2=0,得x1=-1,x2=-2.
当x=-1时,原式无意义,所以x=-1舍去,
当x=-2时,原式=1.【主题升华】
一元二次方程的有关概念
(1)一元二次方程满足的四个条件
(2)一元二次方程的项包括它前面的符号,一次项和常数项可以为0.
(3)根能使方程左右两边相等,已知一个根,可代入确定方程中的字母系数.1.一元二次方程x2-2x-3=0的解是
( )
A.x1=-1,x2=3 B.x1=1,x2=-3
C.x1=-1,x2=-3 D.x1=1,x2=3
【解析】选A.∵a=1,b=-2,c=-3,∴b2-4ac=16,
∴x= ∴x1=-1,x2=3.2.方程(2x+1)(3x-2)=0的解是 .
【解析】∵(2x+1)(3x-2)=0,
∴2x+1=0,3x-2=0,
答案: 3.已知x=-1是关于x的方程2x2+ax-a2=0的一个根,则a= .
【解析】根据题意得:2-a-a2=0,
解得a=-2或1.
答案:-2或14.解方程:x2-10x+9=0.
【解析】将方程x2-10x+9=0,
变形为:x2-10x=-9,
配方,x2-10x+25=-9+25,
整理,得(x-5)2=16,
解得,x1=1,x2=9.【一题多解】公式法:因为a=1,b=-10,c=9,
Δ=100-36=64>0,
由求根公式解得,x1=1,x2=9.
因式分解法:将方程x2-10x+9=0,
变形为:(x-1)(x-9)=0,
解得,x1=1,x2=9.【知识归纳】一元二次方程解法的理论依据及适用形式解读:配方法要先配方,再降次;公式法是判断b2-4ac>0后直接利用求根公式;分解因式法是把方程的一边化为两个一次因式的乘积,另一边为0.主题2 一元二次方程的根与b2-4ac的关系
【主题训练2】已知一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根.
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.【自主解答】(1)∵一元二次方程为x2-(2k+1)x+k2+k=0,
∴Δ=[-(2k+1)]2-4(k2+k)=1>0,
∴此方程有两个不相等的实数根.
(2)∵△ABC的两边AB,AC的长是这个方程的两个实数根,由(1)知,AB≠AC,△ABC的第三边BC的长为5,且△ABC是等腰三角形,
∴必然有AB=5或AC=5,即x=5是原方程的一个解.将x=5代入方程x2-(2k+1)x+k2+k=0,即25-5(2k+1)+k2+k=0,解得k=4或k=5.当k=4时,原方程为x2-9x +20=0,x1=5,x2=4,以5,5,4为边长能构成等腰三角形;
当k=5时,原方程为x2-11x +30=0,x1=5,x2=6,以5,5,6为边长能构成等腰三角形.
∴k的值为4或5.【主题升华】一元二次方程的根与b2-4ac的关系
(1)b2-4ac>0?方程有两个不相等的实数根.
(2)b2-4ac=0?方程有两个相等的实数根.
(3)b2-4ac<0?方程没有实数根.1.下列一元二次方程中,有两个不相等的实数根的方程是( )
A.x2-3x+1=0 B. x2+1=0
C.x2-2x+1=0 D.x2-2x+3=0【解析】选A.选项A中的b2-4ac>0,所以方程有两个不相等的实数根;选项B中的b2-4ac<0,所以方程没有实数根;选项C中的b2-4ac=0,所以方程有两个相等的实数根;选项D中的b2-4ac<0,所以方程没有实数根.2.已知关于x的一元二次方程x2+2x-a=0有两个相等的实数根,则a的值是 ( )
A.4 B.-4 C.1 D.-1
【解析】选D.∵关于x的一元二次方程x2+2x-a=0有两个相等的实数根,
∴Δ=b2-4ac=0,即22-4(-a)=0,解得:a=-1.3.已知关于x的方程x2-2(k-1)x+k2=0有两个实数根,求k的取值范围.
【解析】∵方程x2-2(k-1)x+k2=0有两个实数根,
∴b2-4ac≥0,即[-2(k-1)]2-4k2≥0,
∴4k2-8k+4-4k2≥0,解得k≤ .主题3 一元二次方程的根与系数的关系
【主题训练3】已知α,β是一元二次方程x2-5x-2=0的两个实数根,则α2+αβ+β2的值为 ( )
A.-1 B.9 C.23 D.27【自主解答】选D.∵α,β是一元二次方程x2-5x-2=0的两个实数根∴ ∴α2+αβ+β2=(α+β)2-αβ=52-(-2)=27.【主题升华】一元二次方程的根与系数的关系的三个应用
1.已知一个一元二次方程和它的一个根,不解方程,求另一个根或字母系数的值.
2.已知一个一元二次方程,不解方程,求关于它的两个根的某些代数式的值.
3.利用根与系数的关系求新的方程.1.设x1,x2是方程x2-3x-3=0的两个实数根,则
的值为 ( )
A.5 B.-5 C.1 D.-1【解题指南】本题涉及的三个知识点
(1)一元二次方程根与系数的关系.
(2)分式的运算.
(3)完全平方公式的变形.【解析】选B.由根与系数的关系可知
x1+x2=3,x1x2=-3,
2.已知x=-2是方程x2+mx-6=0的一个根,则方程的另一个根是 .
【解析】设方程另一个根为x1,根据题意得-2·x1=-6,所以x1=3.
答案:3【互动探究】本题中m的值是多少?
【解析】由题意求得方程的两个根分别是-2和3,
∴-2+3=-m,∴m=-1.3.若两个不等实数m,n满足条件:m2-2m-1=0,n2-2n-1=0,则m2+n2的值是 .
【解析】∵m2-2m-1=0,n2-2n-1=0,m≠n,∴m,n是x2-2x-1=0的两根,由根与系数关系得m+n=2,mn=-1,
∴m2+n2=(m+n)2-2mn=22-2×(-1)=6.
答案:64.关于x的一元二次方程x2-(m-3)x-m2=0.
(1)证明:方程总有两个不相等的实数根.
(2)设这个方程的两个实数根为x1,x2,且|x1|=|x2|-2,求m的值及方程的根.
【解析】(1)一元二次方程x2-(m-3)x-m2=0,
∵a=1,b=-(m-3)=3-m,c=-m2,
∴Δ=b2-4ac=(3-m)2-4×1×(-m2)=(3-m)2+4m2>0,
∴方程总有两个不相等的实数根.(2)由根与系数的关系得x1·x2= =-m2≤0,x1+x2=m-3,
∴x1,x2异号,
又|x1|=|x2|-2,即|x1|-|x2|=-2,
若x1>0,x2<0,上式化简得:x1+x2=-2,
∴m-3=-2,即m=1,
方程化为x2+2x-1=0,解得:x1=-1+ ,x2=-1- .
若x1<0,x2>0,上式化简得:-(x1+x2)=-2,
∴x1+x2=m-3=2,即m=5,
方程化为x2-2x-25=0,
解得:x1=1- ,x2=1+ .主题4 一元二次方程的应用
【主题训练4】 “4·20”雅安地震后,某商家为支援灾区人民,计划捐赠帐篷16800顶,该商家备有2辆大货车、8辆小货车运送,计划大货车比小货车每辆每次多运帐篷200顶,大、小货车每天均运送一次,两天恰好运完.
(1)求大、小货车原计划每辆每次各运送帐篷多少顶?(2)因地震导致路基受损,实际运送过程中,每辆大货车每次比
原计划少运200m顶,每辆小货车每次比原计划少运300顶.为了
尽快将帐篷运送到灾区,大货车每天比原计划多跑m次,小货车
每天比原计划多跑 m次,一天刚好运送了帐篷14400顶,求m的
值.【解析】(1)设小货车原计划每辆每次运送帐篷x顶,则大货车
原计划每辆每次运送帐篷(x+200)顶,根据题意,得2[8x+2(x+200)]=16800,解得x=800,
x+200=800+200=1000.
答:大、小货车原计划每辆每次分别运送帐篷1000顶,800顶.(2)根据题意,得
2(1000-200m)+8(800-300)(1+ m)=14400,化简为m2-23m+42=0,解得m1=2,m2=21.
∵1000-200m不能为负数,且 m为整数,
∴m=21不符合实际,舍去,
∴m的值为2.【主题升华】列一元二次方程解应用题的三点注意
1.审题:准确找出已知量与未知量之间的关系.
2.设元:分为直接设未知数和间接设未知数两种,对于直接设未知数列方程比较困难或列出的方程比较复杂时,要考虑采用间接设未知数.
3.检验:求出方程的解后,必须检验所求的解是否符合题目要求或客观实际,不符合的解需要舍去.1.某超市一月份的营业额为36万元,三月
份的营业额为48万元.设每月的平均增长率为x,则可列方程
为 ( )
A.48(1-x)2=36 B.48(1+x)2=36
C.36(1-x)2=48 D.36(1+x)2=48
【解析】选D.二月份的营业额为36(1+x),三月份的营业额为36(1+x)(1+x)=36(1+x)2,
即所列的方程为36(1+x)2=48.2.三角形的两边长分别为3和6,第三边是方程x2-6x+8=0的解,这个三角形的周长是 ( )
A.11 B.13 C.11或13 D.11和13
【解析】选B.解方程x2-6x+8=0,得x1=2,x2=4.∵2+3<6,∴第三边不能为2,当第三边为4时,周长为3+6+4=13.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
