人教版高中数学2019-2020 选修二 2-1 第二章 2.2.3 双曲线的几何性质 课件(共22张PPT)
文档属性
| 名称 | 人教版高中数学2019-2020 选修二 2-1 第二章 2.2.3 双曲线的几何性质 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1004.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
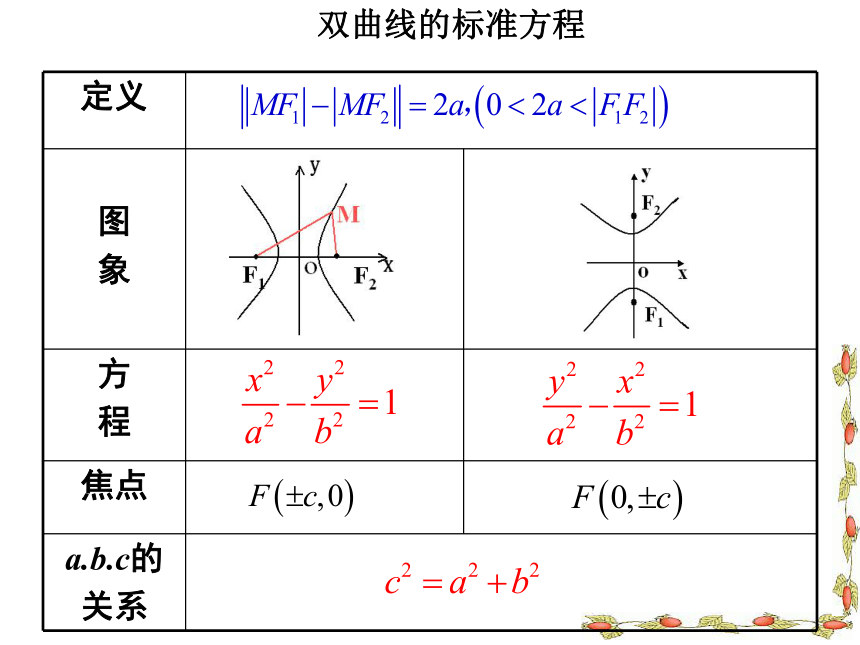
双曲线的标准方程
定义
图
象
方
程
焦点
a.b.c的
关系
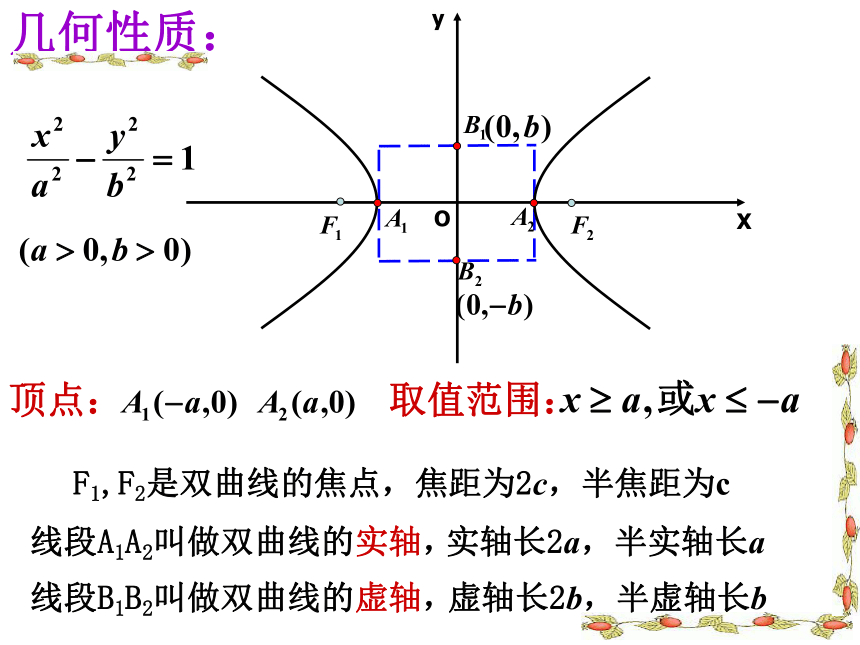
几何性质:
顶点:
取值范围:
线段A1A2叫做双曲线的实轴,
线段B1B2叫做双曲线的虚轴,
F1,F2是双曲线的焦点,焦距为2c,半焦距为c
实轴长2a,半实轴长a
虚轴长2b,半虚轴长b
几何性质:
对称性:
双曲线关于x轴、y轴、原点对称
渐近线:
实轴和虚轴相等的双曲线叫等轴双曲线
几何性质:
离心率:
思考:
(1) 双曲线的离心率的范围是什么?
(2)上图中表示a,b,c的线段分别是哪些?
(3)当离心率变化时,双曲线的形状如何变化?
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)
(c,0)、(-c,0)
半实轴长为a,
半虚轴长为b.
c2=a2+b2
同前
(0,a)、(0,-a)
(0 , c)、(0, -c)
同前
同前
同前
渐近线
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a,b,c的关系
(1)双曲线9y2-16x2=144的实半轴长是 ,
虚轴长是 , 焦点坐标是 , 离心
率为 ,渐近线方程是 .
4
6
例题1:
(2)求符合下列条件的双曲线的标准方程:
例题2:
例题2:
例题3:
关于坐标
轴和
原点
都对
称
例4 :
例3 :
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
法二:巧设方程,运用待定系数法.
设双曲线方程为
练:
例6、双曲线型自然通风塔的外形,是双曲线
的一部分绕其虚轴旋转所成的曲面,它的
最小半径为12m,上口半径为13m,下口半径
为25m,高55m.选择适当的坐标系,求出此
双曲线的方程(精确到1m).
A′
A
0
x
C′
C
B′
B
y
例题讲解
y
0
直线与双曲线问题:
直线与双曲线问题:
直线与双曲线问题:
例10、过双曲线 的右焦点 倾斜角为
的直线交双曲线于A,B两点,求弦长|AB|
直线与双曲线的位置关系:
例11、由双曲线 上的一点P与左、右
两焦点 构成 ,求 的内切圆与
边 的切点坐标。
双曲线的标准方程
定义
图
象
方
程
焦点
a.b.c的
关系
几何性质:
顶点:
取值范围:
线段A1A2叫做双曲线的实轴,
线段B1B2叫做双曲线的虚轴,
F1,F2是双曲线的焦点,焦距为2c,半焦距为c
实轴长2a,半实轴长a
虚轴长2b,半虚轴长b
几何性质:
对称性:
双曲线关于x轴、y轴、原点对称
渐近线:
实轴和虚轴相等的双曲线叫等轴双曲线
几何性质:
离心率:
思考:
(1) 双曲线的离心率的范围是什么?
(2)上图中表示a,b,c的线段分别是哪些?
(3)当离心率变化时,双曲线的形状如何变化?
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)
(c,0)、(-c,0)
半实轴长为a,
半虚轴长为b.
c2=a2+b2
同前
(0,a)、(0,-a)
(0 , c)、(0, -c)
同前
同前
同前
渐近线
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a,b,c的关系
(1)双曲线9y2-16x2=144的实半轴长是 ,
虚轴长是 , 焦点坐标是 , 离心
率为 ,渐近线方程是 .
4
6
例题1:
(2)求符合下列条件的双曲线的标准方程:
例题2:
例题2:
例题3:
关于坐标
轴和
原点
都对
称
例4 :
例3 :
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
法二:巧设方程,运用待定系数法.
设双曲线方程为
练:
例6、双曲线型自然通风塔的外形,是双曲线
的一部分绕其虚轴旋转所成的曲面,它的
最小半径为12m,上口半径为13m,下口半径
为25m,高55m.选择适当的坐标系,求出此
双曲线的方程(精确到1m).
A′
A
0
x
C′
C
B′
B
y
例题讲解
y
0
直线与双曲线问题:
直线与双曲线问题:
直线与双曲线问题:
例10、过双曲线 的右焦点 倾斜角为
的直线交双曲线于A,B两点,求弦长|AB|
直线与双曲线的位置关系:
例11、由双曲线 上的一点P与左、右
两焦点 构成 ,求 的内切圆与
边 的切点坐标。
