2020湘教版八下数学第2章四边形2.1多边形教学课件(43张PPT)
文档属性
| 名称 | 2020湘教版八下数学第2章四边形2.1多边形教学课件(43张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 08:38:41 | ||
图片预览




文档简介
课件43张PPT。第2章 四边形
2.1 多边形1.通过具体情境了解多边形的概念,掌握四边形和多边形的内角和,会利用多边形的内角和进行计算.
2.通过多边形内角和公式的推导过程,培养学生的发散思维能力,逐步提高推理的能力.
3.了解多边形外角和的概念、掌握多边形外角和公式.
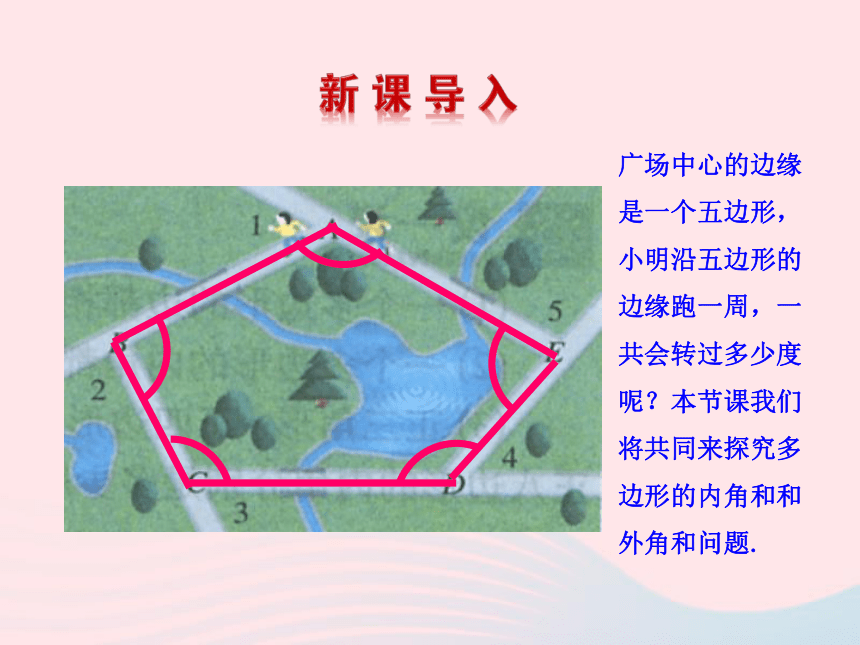
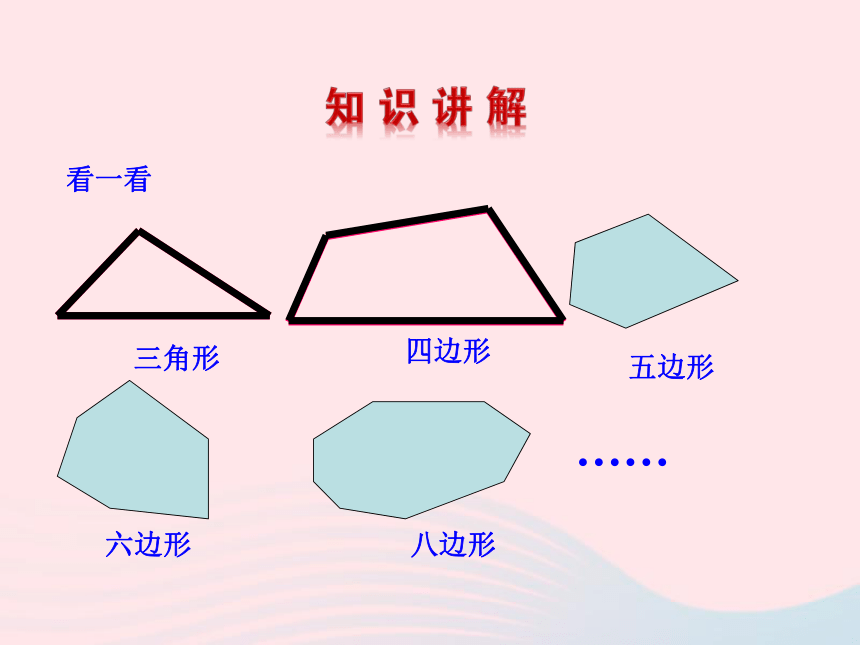
4.了解正多边形的概念;了解四边形的不稳定性及生活中的应用.广场中心的边缘是一个五边形,小明沿五边形的边缘跑一周,一共会转过多少度呢?本节课我们将共同来探究多边形的内角和和外角和问题.看一看四边形五边形六边形八边形……三角形顶点内角边对角线
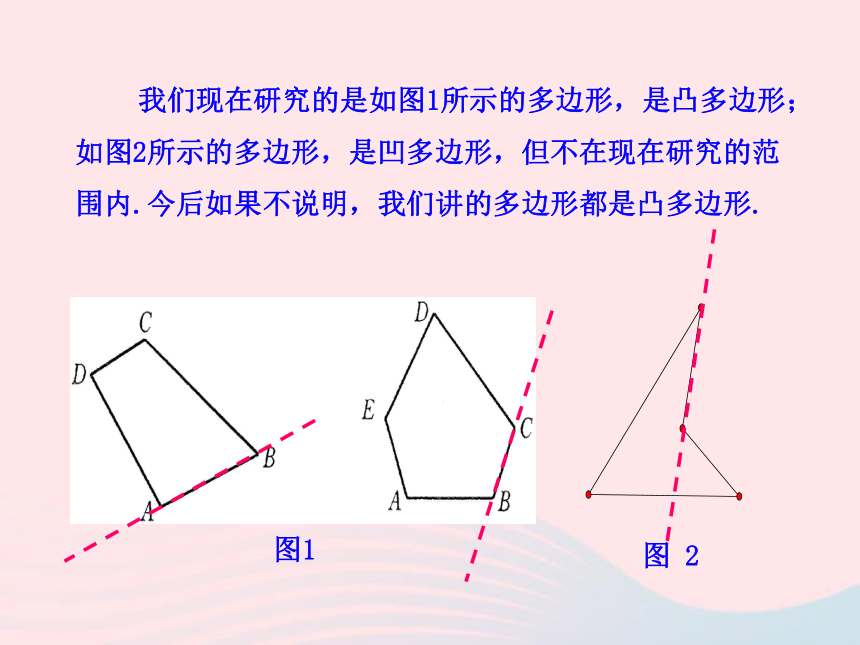
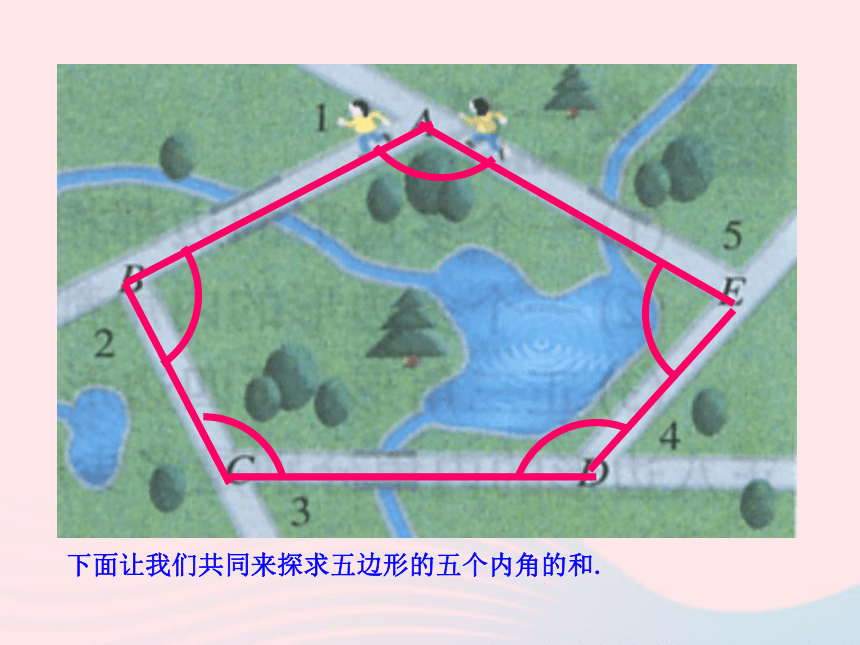
(连接不相邻两个顶点的线段)这里所说的多边形都指凸多边形在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.图 2 我们现在研究的是如图1所示的多边形,是凸多边形;如图2所示的多边形,是凹多边形,但不在现在研究的范围内.今后如果不说明,我们讲的多边形都是凸多边形.下面让我们共同来探求五边形的五个内角的和. A BCDE我们知道,三角形的内角和等于______度,四边形的内角和等于 度,那五边形的内角和呢?180360你能动手做一做吗?
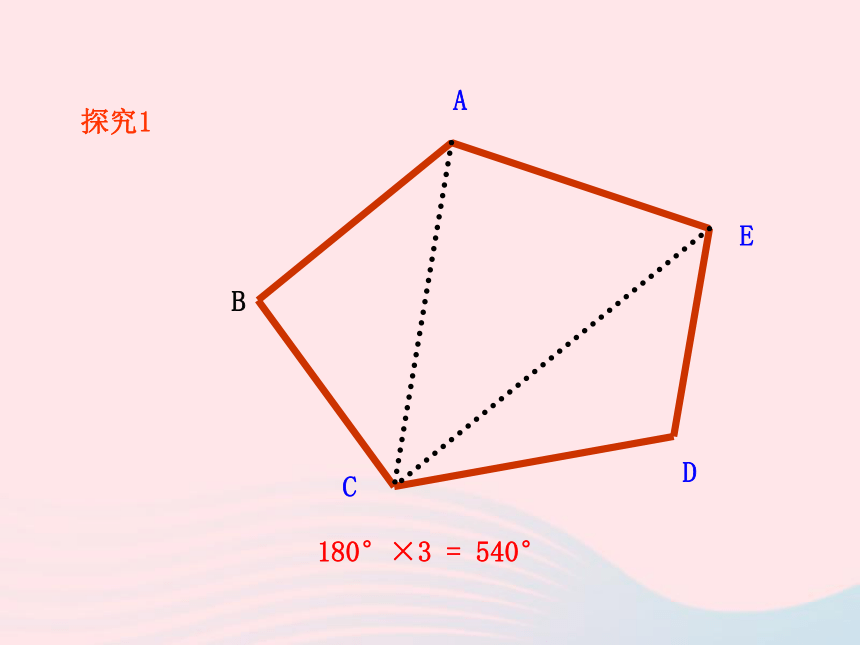
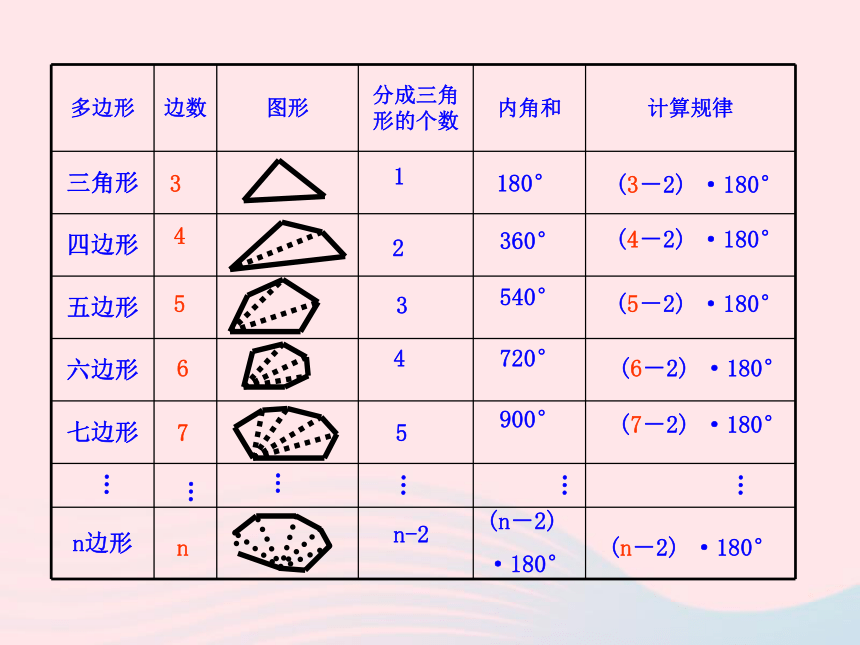
你能想出几种不同的解法? A BCDE探究1180°×3 = 540°………………34567n1n-22345180°360°540°720°900°(n-2)
·180°(n-2) ·180°(7-2) ·180°(6-2) ·180°(5-2) ·180°(4-2) ·180°(3-2) ·180°E
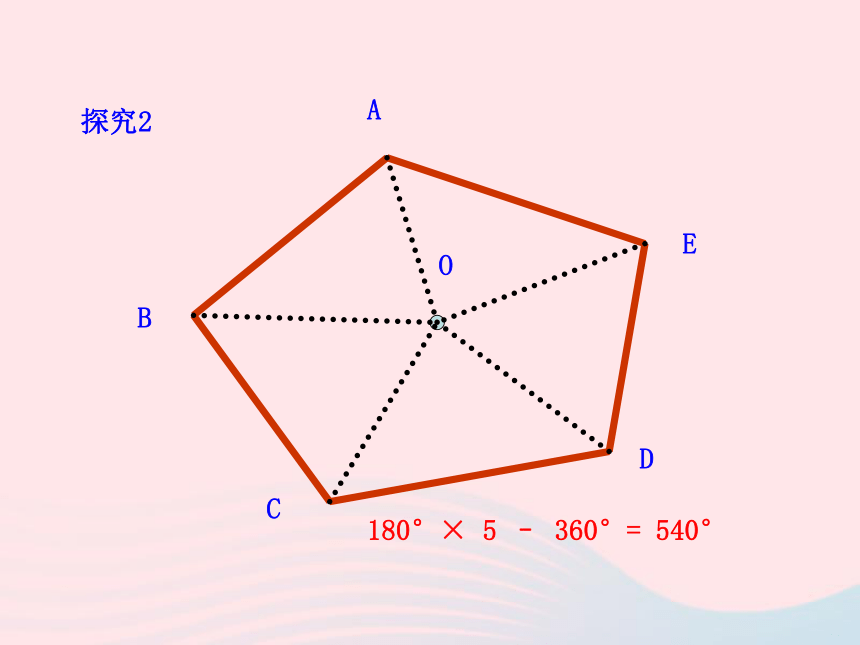
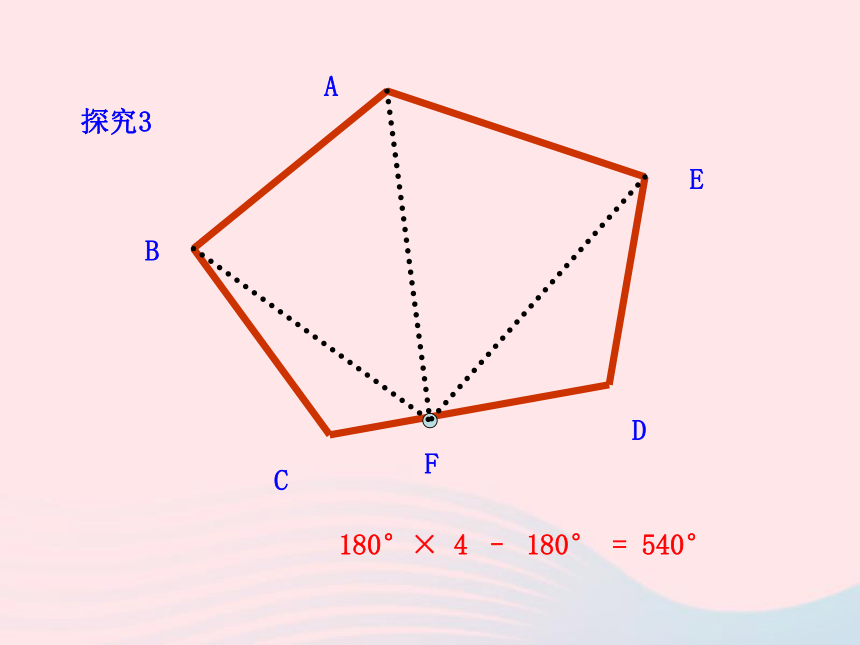
ABCDO180°× 5 – 360°= 540°探究2ABCDEF180°× 4 – 180° = 540°探究3 A BCDE180°+ 360° = 540°探究42.如图:(1)作多边形过顶点A的所有对角线,并分别用字母表达出来。(2)求这个多边形的内角和。ABCDEF1.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?
答案:七边形 900°解:(1)过顶点A的对角线共有三 条,分别是AC、AD和AE. (2)这个多边形的内角和是:
(6-2) · 180 = 720(度).【跟踪训练】解:由多边形的内角和公式可得:(n-2)·180 = 1440 (n - 2) = 8n = 10所以这是十边形。十3.如果一个多边形的内角和是1440度,那么这是___边形。在平面内,内角都相等、边也都相等的多边形叫作正多边形.正三角形正方形正五边形正六边形正八边形观察图中的多边形,它们的边、角有什么特点?(1)一个多边形的边都相等,它的内角一定都相等吗?(2)一个多边形的内角都相等,它的边一定都相等吗? (3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?正n边形呢?菱形(分别是60°,90°,108°,120°,135°, )矩形不一定,如菱形.不一定,如矩形.2.若正n边形的一个内角是144度,则n=_______.解:由多边形的内角和公式可得:(n -2) · 180 = 144n180n – 360 = 144n180n -144n=36036n = 360n = 10101.如果十二边形的每一个内角都相等,那么每个内角是
______度。150【跟踪训练】3.在四边形ABCD中,∠A=120度,∠B︰∠C︰∠D=3︰4︰5,求∠B,∠C,∠D的度数.解:设∠B,∠C,∠D的度数分别是3x, 4x, 5x度,由四边形的内角和等于360度可得: 120 + 3x + 4x + 5x = 360 12x = 240 x = 20所以 3x = 60
4x = 80
5x = 100答:∠B,∠C,∠D的度数分别为60度,80度,100度.(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出?1+?2+?3+?4+?5=?吗?你是
怎样得到的?4.问题解决
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
ABCDEA'
C'
D'
E'B'
O2345112 345结论:(1)分别是?1,?2,?3,?4,?5
(2)角度之和为360°
(3)?1,?2,?3,?4,?5的和等于360°如果广场的形状是六边形、八边形,那么还有类似的结论吗?多边形内角的一边与另一边的反向延长线所组成的角叫作这个多边形的外角.
在每个顶点处取这个多边形的一个外角,它们的和叫作这个多边形的外角和.
任意多边形的外角和都等于360°
(1)还有什么方法可以推导出多边形的外角和公式?
(2)利用多边形外角和的结论,能否推导出多边形内角和的结论?例 一个多边形的内角和等于它的外角和的3倍,它是几边形?解:设这个多边形是n边形,由题意得
(n-2)·180=360×3
解得 n=8
答:这个多边形是八边形.【例题】【解析】答案:【跟踪训练】【解析】【解析】2.(自贡·中考)一个多边形截取一个角后,形成的另一个多边形的内角和是1 620°,则原来多边形的边数是( )
(A)10 (B)11
(C)12 (D)以上都有可能【解析】选D.设截去一个角后的多边形的边数为n,则有
(n-2)×180°=1 620°解得n=11,
由于多边形被截取一个角后有三种情况,一是边数减少一条,二是边数不变,三是边数增加一条,所以多边形的边数可能是10,11,12.3.如图,能够利用下面图形说明n边形的内角和为
(n-2)·180°的有( )
(A)1个 (B)2个 (C)3个 (D)4个【解析】选D.探索多边形内角和的思路是把多边形划分成三角形,利用三角形的内角和为180°求得,由图形作法可知:
图①为n·180°-360°=(n-2)×180°,
图②为(n-2)×180°,
图③为(n-1)×180°-180°=(n-2)×180°,
图④为(n-1)×180°-180°=(n-2)×180°.4.(湛江·中考)如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
(A)30° (B)40°
(C)80° (D)不存在【解析】选B.观察图形分析已知条件,不难看出小林实
际上围绕正多边形走了一周,并且该正多边形的边长是
12米,因为小林一共走了108米,即该正多边形的周长
是108米,所以其边数为9,因其外角和是定值360°,
故α= =40°,所以本题选B.【解析】答案:【解析】答案:7.(宿迁·中考)如图,平面上两个正方形与一个正五边形都有一条公共边,则∠α=_________.
【解析】∠α=360°-180°-108°=72°
答案:72°.8.(晋江·中考)将一块正五边形纸片(图①)做成一个底面仍为正五边形且高相等的无盖纸盒(侧面均垂直于底面,见图②),需在每一个顶点处剪去一个四边形,例如图①中的四边形ABCD,则∠BAD的大小是________.【解析】要做成一个底面仍为正五边形且高相等的无盖纸盒,则AB,AD都与里面的正五边形的边垂直,所以∠BAD与正五边形的内角互补,∠BAD=180°-108°=72°
答案:72°9.如图,∠A,∠B,∠C,∠D,∠E,∠F的度数之和为________.【解析】如图,连结AD,
由∠3=∠4,得∠1+∠2=∠E+∠F,
所以∠BAF+∠B+∠C+∠EDC+∠E+∠F
=∠5+∠B+∠C+∠6+∠1+∠2
=四边形ABCD的内角和=360°
答案:360°10.多边形的每个内角都等于它的相邻外角的6倍,试求该多边形的边数.
【解析】设多边形的边数为n,
则(n-2)·180°=6×360°,
解得n=14.本节课我们研究了多边形的定义及其内角和、外角和公式.
1.多边形的内角和公式:n边形的内角和等于(n-2)·
180°,它揭示了多边形内角和与边数之间的关系.
2.多边形的外角及其外角和公式:多边形的外角和等于360°.
求解有关多边形的角的计算题,有时直接应用外角和公式会比较简便.人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定、冷静,学习如何从慌乱中找到生机.
2.1 多边形1.通过具体情境了解多边形的概念,掌握四边形和多边形的内角和,会利用多边形的内角和进行计算.
2.通过多边形内角和公式的推导过程,培养学生的发散思维能力,逐步提高推理的能力.
3.了解多边形外角和的概念、掌握多边形外角和公式.
4.了解正多边形的概念;了解四边形的不稳定性及生活中的应用.广场中心的边缘是一个五边形,小明沿五边形的边缘跑一周,一共会转过多少度呢?本节课我们将共同来探究多边形的内角和和外角和问题.看一看四边形五边形六边形八边形……三角形顶点内角边对角线
(连接不相邻两个顶点的线段)这里所说的多边形都指凸多边形在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.图 2 我们现在研究的是如图1所示的多边形,是凸多边形;如图2所示的多边形,是凹多边形,但不在现在研究的范围内.今后如果不说明,我们讲的多边形都是凸多边形.下面让我们共同来探求五边形的五个内角的和. A BCDE我们知道,三角形的内角和等于______度,四边形的内角和等于 度,那五边形的内角和呢?180360你能动手做一做吗?
你能想出几种不同的解法? A BCDE探究1180°×3 = 540°………………34567n1n-22345180°360°540°720°900°(n-2)
·180°(n-2) ·180°(7-2) ·180°(6-2) ·180°(5-2) ·180°(4-2) ·180°(3-2) ·180°E
ABCDO180°× 5 – 360°= 540°探究2ABCDEF180°× 4 – 180° = 540°探究3 A BCDE180°+ 360° = 540°探究42.如图:(1)作多边形过顶点A的所有对角线,并分别用字母表达出来。(2)求这个多边形的内角和。ABCDEF1.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?
答案:七边形 900°解:(1)过顶点A的对角线共有三 条,分别是AC、AD和AE. (2)这个多边形的内角和是:
(6-2) · 180 = 720(度).【跟踪训练】解:由多边形的内角和公式可得:(n-2)·180 = 1440 (n - 2) = 8n = 10所以这是十边形。十3.如果一个多边形的内角和是1440度,那么这是___边形。在平面内,内角都相等、边也都相等的多边形叫作正多边形.正三角形正方形正五边形正六边形正八边形观察图中的多边形,它们的边、角有什么特点?(1)一个多边形的边都相等,它的内角一定都相等吗?(2)一个多边形的内角都相等,它的边一定都相等吗? (3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?正n边形呢?菱形(分别是60°,90°,108°,120°,135°, )矩形不一定,如菱形.不一定,如矩形.2.若正n边形的一个内角是144度,则n=_______.解:由多边形的内角和公式可得:(n -2) · 180 = 144n180n – 360 = 144n180n -144n=36036n = 360n = 10101.如果十二边形的每一个内角都相等,那么每个内角是
______度。150【跟踪训练】3.在四边形ABCD中,∠A=120度,∠B︰∠C︰∠D=3︰4︰5,求∠B,∠C,∠D的度数.解:设∠B,∠C,∠D的度数分别是3x, 4x, 5x度,由四边形的内角和等于360度可得: 120 + 3x + 4x + 5x = 360 12x = 240 x = 20所以 3x = 60
4x = 80
5x = 100答:∠B,∠C,∠D的度数分别为60度,80度,100度.(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出?1+?2+?3+?4+?5=?吗?你是
怎样得到的?4.问题解决
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
ABCDEA'
C'
D'
E'B'
O2345112 345结论:(1)分别是?1,?2,?3,?4,?5
(2)角度之和为360°
(3)?1,?2,?3,?4,?5的和等于360°如果广场的形状是六边形、八边形,那么还有类似的结论吗?多边形内角的一边与另一边的反向延长线所组成的角叫作这个多边形的外角.
在每个顶点处取这个多边形的一个外角,它们的和叫作这个多边形的外角和.
任意多边形的外角和都等于360°
(1)还有什么方法可以推导出多边形的外角和公式?
(2)利用多边形外角和的结论,能否推导出多边形内角和的结论?例 一个多边形的内角和等于它的外角和的3倍,它是几边形?解:设这个多边形是n边形,由题意得
(n-2)·180=360×3
解得 n=8
答:这个多边形是八边形.【例题】【解析】答案:【跟踪训练】【解析】【解析】2.(自贡·中考)一个多边形截取一个角后,形成的另一个多边形的内角和是1 620°,则原来多边形的边数是( )
(A)10 (B)11
(C)12 (D)以上都有可能【解析】选D.设截去一个角后的多边形的边数为n,则有
(n-2)×180°=1 620°解得n=11,
由于多边形被截取一个角后有三种情况,一是边数减少一条,二是边数不变,三是边数增加一条,所以多边形的边数可能是10,11,12.3.如图,能够利用下面图形说明n边形的内角和为
(n-2)·180°的有( )
(A)1个 (B)2个 (C)3个 (D)4个【解析】选D.探索多边形内角和的思路是把多边形划分成三角形,利用三角形的内角和为180°求得,由图形作法可知:
图①为n·180°-360°=(n-2)×180°,
图②为(n-2)×180°,
图③为(n-1)×180°-180°=(n-2)×180°,
图④为(n-1)×180°-180°=(n-2)×180°.4.(湛江·中考)如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
(A)30° (B)40°
(C)80° (D)不存在【解析】选B.观察图形分析已知条件,不难看出小林实
际上围绕正多边形走了一周,并且该正多边形的边长是
12米,因为小林一共走了108米,即该正多边形的周长
是108米,所以其边数为9,因其外角和是定值360°,
故α= =40°,所以本题选B.【解析】答案:【解析】答案:7.(宿迁·中考)如图,平面上两个正方形与一个正五边形都有一条公共边,则∠α=_________.
【解析】∠α=360°-180°-108°=72°
答案:72°.8.(晋江·中考)将一块正五边形纸片(图①)做成一个底面仍为正五边形且高相等的无盖纸盒(侧面均垂直于底面,见图②),需在每一个顶点处剪去一个四边形,例如图①中的四边形ABCD,则∠BAD的大小是________.【解析】要做成一个底面仍为正五边形且高相等的无盖纸盒,则AB,AD都与里面的正五边形的边垂直,所以∠BAD与正五边形的内角互补,∠BAD=180°-108°=72°
答案:72°9.如图,∠A,∠B,∠C,∠D,∠E,∠F的度数之和为________.【解析】如图,连结AD,
由∠3=∠4,得∠1+∠2=∠E+∠F,
所以∠BAF+∠B+∠C+∠EDC+∠E+∠F
=∠5+∠B+∠C+∠6+∠1+∠2
=四边形ABCD的内角和=360°
答案:360°10.多边形的每个内角都等于它的相邻外角的6倍,试求该多边形的边数.
【解析】设多边形的边数为n,
则(n-2)·180°=6×360°,
解得n=14.本节课我们研究了多边形的定义及其内角和、外角和公式.
1.多边形的内角和公式:n边形的内角和等于(n-2)·
180°,它揭示了多边形内角和与边数之间的关系.
2.多边形的外角及其外角和公式:多边形的外角和等于360°.
求解有关多边形的角的计算题,有时直接应用外角和公式会比较简便.人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定、冷静,学习如何从慌乱中找到生机.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
