湘教版八下数学2.5.1矩形的性质教学课件(33张PPT)
文档属性
| 名称 | 湘教版八下数学2.5.1矩形的性质教学课件(33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览





文档简介
课件33张PPT。2.5 矩形
2.5.1 矩形的性质1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
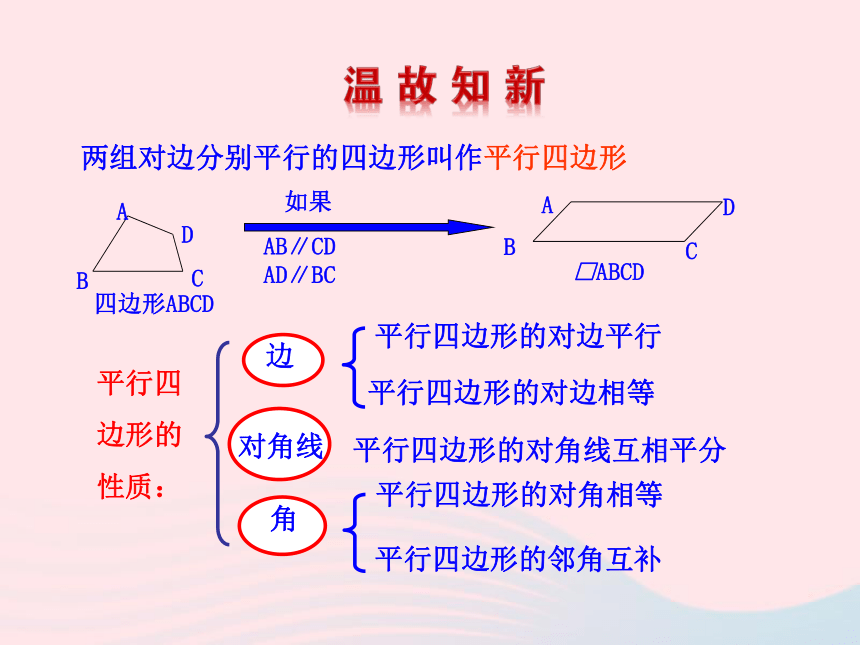
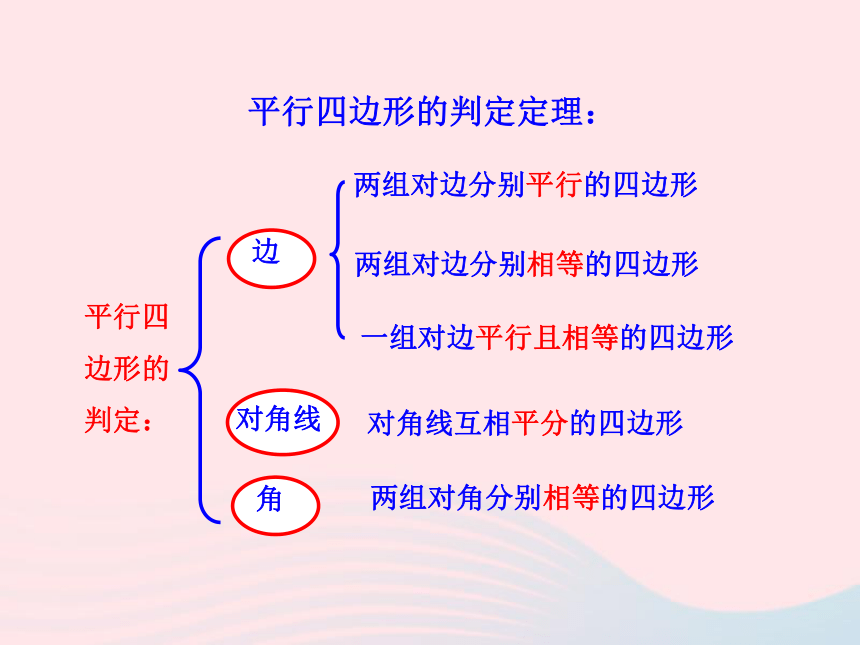
2.会初步运用矩形的性质等知识,解决简单的证明和计算,进一步培养学生的分析能力.两组对边分别平行的四边形叫作平行四边形平行四边形的性质:平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的对角线互相平分平行四边形的判定:两组对边分别平行的四边形两组对边分别相等的四边形两组对角分别相等的四边形对角线互相平分的四边形一组对边平行且相等的四边形平行四边形的判定定理:有一个角
是直角两组对边
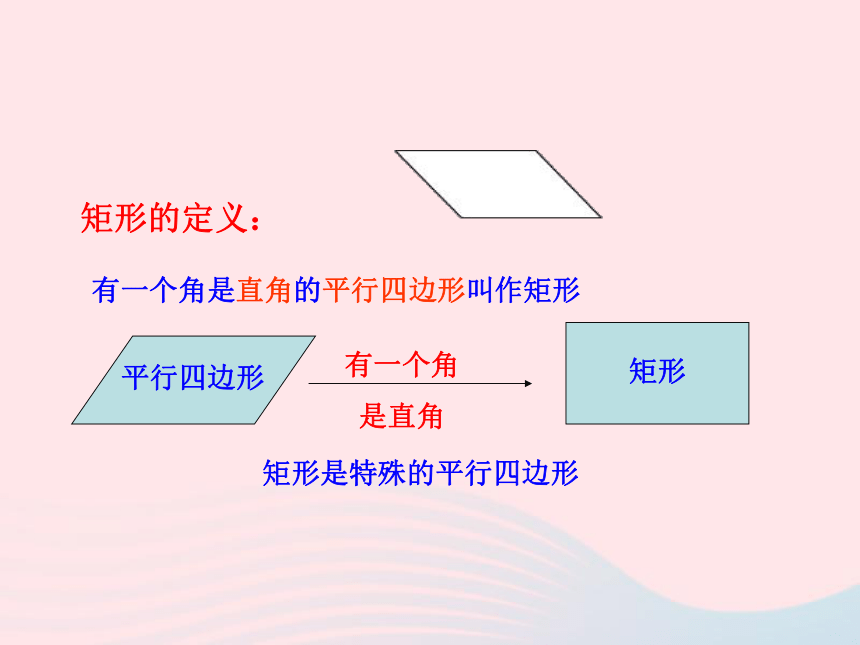
分别平行矩形 我们已经知道平行四边形是特殊的四边形,因此平行
四边形除具有四边形的性质外,还有它的特殊性质,同
样,对于平行四边形来说也有特殊情况即特殊的平行四边
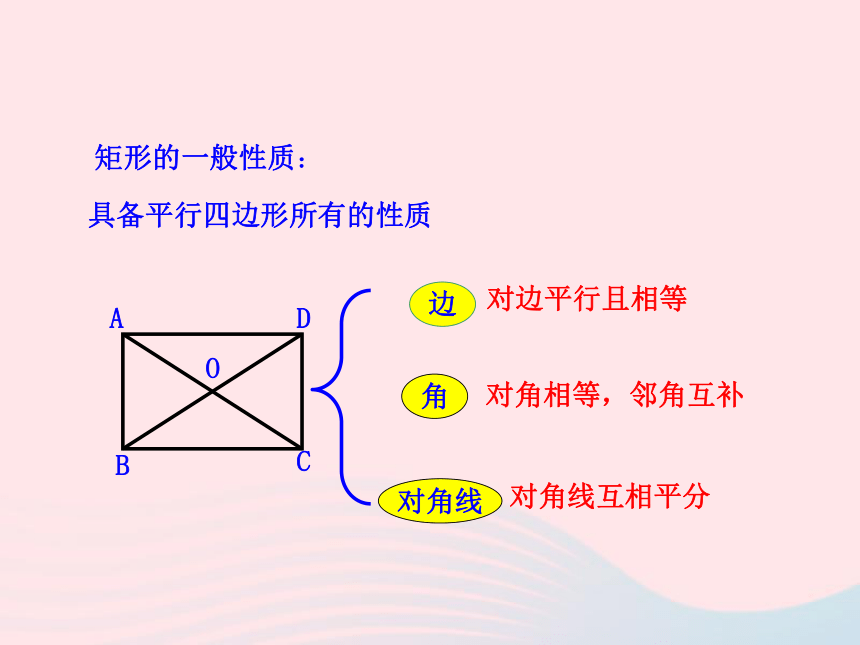
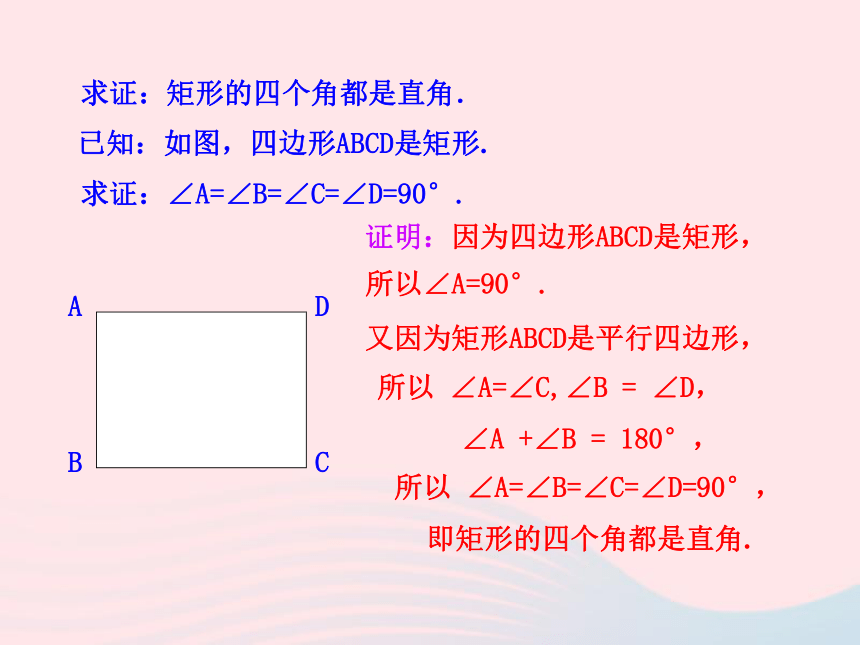
形,这堂课我们就来研究一种特殊的平行四边形— 矩形有一个角是直角的平行四边形叫作矩形矩形的定义:矩形是特殊的平行四边形具备平行四边形所有的性质对边平行且相等对角相等,邻角互补对角线互相平分矩形的一般性质:矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.求证:∠A=∠B=∠C=∠D=90°.证明:因为四边形ABCD是矩形,所以∠A=90°.又因为矩形ABCD是平行四边形,所以 ∠A=∠C,∠B = ∠D,
∠A +∠B = 180°,所以 ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.
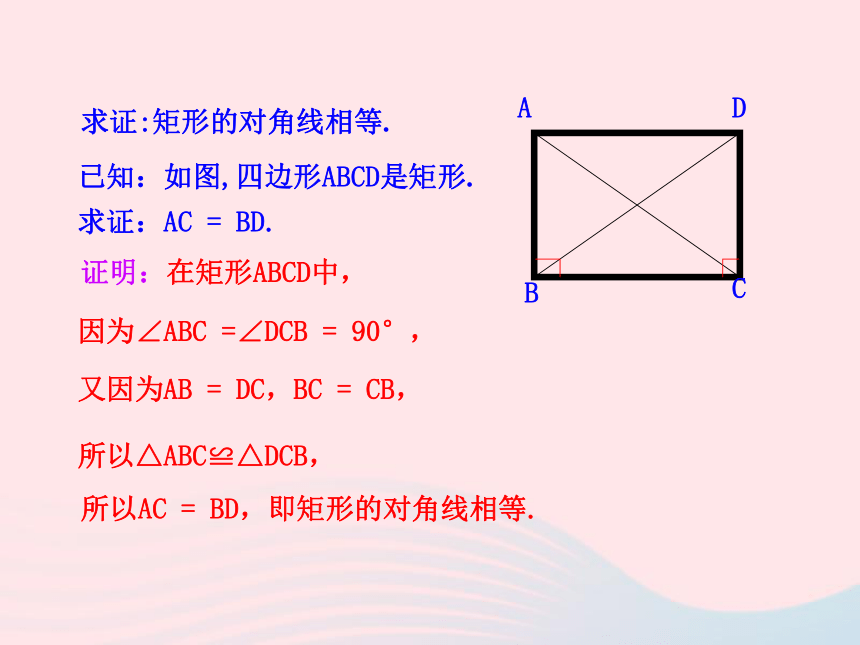
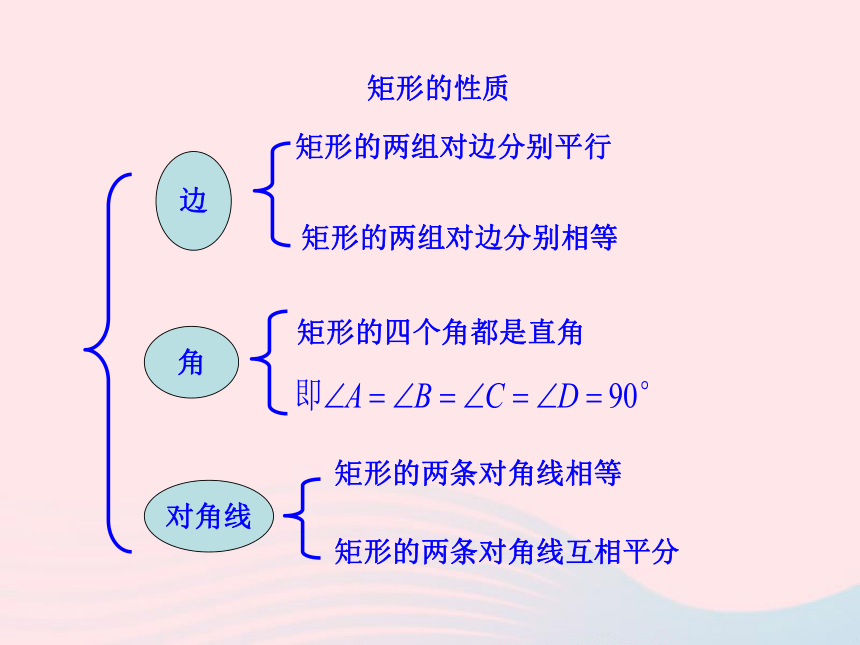
求证:AC = BD.证明:在矩形ABCD中,因为∠ABC =∠DCB = 90°,又因为AB = DC,BC = CB,所以△ABC≌△DCB,所以AC = BD,即矩形的对角线相等.求证:矩形的对角线相等.矩形的特殊性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形的两条对角线相等边对角线角矩形的性质例 : 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?所以AC与BD相等且互相平分,所以OA=OB.因为∠AOB=60°,所以△AOB是等边三角形,所以OA=AB=4(㎝),所以矩形对角线的长AC=BD=2OA=8(㎝).解:因为四边形ABCD是矩形,【例题】下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直D 【跟踪训练】2.过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是( )
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互相垂直且平分的四边形
D.对角线垂直的四边形D3. 已知矩形的一条对角线与一边的夹角是40°,则两条
对角线所夹锐角的度数为( )
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等
于( )
A.30° B.45° C.60° D.120°DA矩形的对称性
矩形是轴对称图形,过每一组对边的中点的直线都是矩
形的对称轴.
矩形是中心对称图形,对角线的交点是它的对称中心.四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?OABCD公平,因为OA=OC=OB=OD【跟踪训练】直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半应用格式:因为在Rt△ABC中,∠ABC=90°,BO是AC上
的中线.
所以BO = AC.已知△ABC是Rt△,∠ABC=90°,BD是斜边AC上的中线(1)若BD=3㎝ 则AC=_____㎝
(2)若∠C=30°,AB=5㎝,则AC=____㎝,BD=___㎝.6510【跟踪训练】【解析】2.(温州·中考)如图,AC,BD是矩形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有( )
(A)1个 (B)2个 (C)3个 (D)4个
【解析】选D.与△ABC全等的三角形有:△DCB、△BAD、△CDA、△DCE共4个.3.(哈尔滨·中考)如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为_____度 .【解析】由折叠可知,∠DEF=∠BEF.
∠EFC=∠EFC′.
因为四边形ABCD是矩形,
所以∠A=∠D=∠C=90°.
又∠ABE=20°,
所以∠AEB=70°,
所以∠DEF=55°.
在四边形EFCD中,∠EFC=125°,
所以∠EFC′=125°.
答案:1254.(河北·中考)如图,矩形ABCD的顶点A,B在数
轴上,CD=6,点A对应的数为-1,则点B所对应的数为
________.
【解析】在矩形ABCD中,CD=6,
所以AB=6.
又点A对应的数为-1,
所以点B所对应的数为5.
答案:55.如图,矩形ABCD的两对角线交于点O,
过点O作AC的垂线EF,分别交AD,BC于
点E,F,连接CE,已知△CDE的周长为
24 cm,则矩形ABCD的周长是_____cm.
【解析】易得EF垂直平分AC,
所以EA=EC.
因为△CDE的周长为24 cm,
所以DC+DA=24 cm,
所以矩形ABCD的周长为48 cm.
答案:486.(黄冈·中考)如图,矩形纸片ABCD,AB=5 cm,BC=
10 cm,CD上有一点E,ED=2 cm,AD上有一点P,PD=
3 cm,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点
重合,折痕与PF交于Q点,则PQ的长是____cm.【解析】如图连结EQ,作QM⊥CD于M,
由题意知EQ=PQ=DM,
设PQ=x,则MQ=PD=3.
ME=DM-DE=x-2,
在Rt△MQE中(x-2)2+32=x2
解得x= (cm)
答案: 【解析】本节课主要学习了矩形的定义、性质,要求我们
1.弄清矩形的性质与平行四边形性质的区别与联系.
2.会应用矩形的性质证明一些几何问题.人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定、冷静,学习如何从慌乱中找到生机。
——席慕蓉
2.5.1 矩形的性质1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的性质等知识,解决简单的证明和计算,进一步培养学生的分析能力.两组对边分别平行的四边形叫作平行四边形平行四边形的性质:平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的对角线互相平分平行四边形的判定:两组对边分别平行的四边形两组对边分别相等的四边形两组对角分别相等的四边形对角线互相平分的四边形一组对边平行且相等的四边形平行四边形的判定定理:有一个角
是直角两组对边
分别平行矩形 我们已经知道平行四边形是特殊的四边形,因此平行
四边形除具有四边形的性质外,还有它的特殊性质,同
样,对于平行四边形来说也有特殊情况即特殊的平行四边
形,这堂课我们就来研究一种特殊的平行四边形— 矩形有一个角是直角的平行四边形叫作矩形矩形的定义:矩形是特殊的平行四边形具备平行四边形所有的性质对边平行且相等对角相等,邻角互补对角线互相平分矩形的一般性质:矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.求证:∠A=∠B=∠C=∠D=90°.证明:因为四边形ABCD是矩形,所以∠A=90°.又因为矩形ABCD是平行四边形,所以 ∠A=∠C,∠B = ∠D,
∠A +∠B = 180°,所以 ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.
求证:AC = BD.证明:在矩形ABCD中,因为∠ABC =∠DCB = 90°,又因为AB = DC,BC = CB,所以△ABC≌△DCB,所以AC = BD,即矩形的对角线相等.求证:矩形的对角线相等.矩形的特殊性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形的两条对角线相等边对角线角矩形的性质例 : 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?所以AC与BD相等且互相平分,所以OA=OB.因为∠AOB=60°,所以△AOB是等边三角形,所以OA=AB=4(㎝),所以矩形对角线的长AC=BD=2OA=8(㎝).解:因为四边形ABCD是矩形,【例题】下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直D 【跟踪训练】2.过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是( )
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互相垂直且平分的四边形
D.对角线垂直的四边形D3. 已知矩形的一条对角线与一边的夹角是40°,则两条
对角线所夹锐角的度数为( )
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等
于( )
A.30° B.45° C.60° D.120°DA矩形的对称性
矩形是轴对称图形,过每一组对边的中点的直线都是矩
形的对称轴.
矩形是中心对称图形,对角线的交点是它的对称中心.四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?OABCD公平,因为OA=OC=OB=OD【跟踪训练】直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半应用格式:因为在Rt△ABC中,∠ABC=90°,BO是AC上
的中线.
所以BO = AC.已知△ABC是Rt△,∠ABC=90°,BD是斜边AC上的中线(1)若BD=3㎝ 则AC=_____㎝
(2)若∠C=30°,AB=5㎝,则AC=____㎝,BD=___㎝.6510【跟踪训练】【解析】2.(温州·中考)如图,AC,BD是矩形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有( )
(A)1个 (B)2个 (C)3个 (D)4个
【解析】选D.与△ABC全等的三角形有:△DCB、△BAD、△CDA、△DCE共4个.3.(哈尔滨·中考)如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为_____度 .【解析】由折叠可知,∠DEF=∠BEF.
∠EFC=∠EFC′.
因为四边形ABCD是矩形,
所以∠A=∠D=∠C=90°.
又∠ABE=20°,
所以∠AEB=70°,
所以∠DEF=55°.
在四边形EFCD中,∠EFC=125°,
所以∠EFC′=125°.
答案:1254.(河北·中考)如图,矩形ABCD的顶点A,B在数
轴上,CD=6,点A对应的数为-1,则点B所对应的数为
________.
【解析】在矩形ABCD中,CD=6,
所以AB=6.
又点A对应的数为-1,
所以点B所对应的数为5.
答案:55.如图,矩形ABCD的两对角线交于点O,
过点O作AC的垂线EF,分别交AD,BC于
点E,F,连接CE,已知△CDE的周长为
24 cm,则矩形ABCD的周长是_____cm.
【解析】易得EF垂直平分AC,
所以EA=EC.
因为△CDE的周长为24 cm,
所以DC+DA=24 cm,
所以矩形ABCD的周长为48 cm.
答案:486.(黄冈·中考)如图,矩形纸片ABCD,AB=5 cm,BC=
10 cm,CD上有一点E,ED=2 cm,AD上有一点P,PD=
3 cm,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点
重合,折痕与PF交于Q点,则PQ的长是____cm.【解析】如图连结EQ,作QM⊥CD于M,
由题意知EQ=PQ=DM,
设PQ=x,则MQ=PD=3.
ME=DM-DE=x-2,
在Rt△MQE中(x-2)2+32=x2
解得x= (cm)
答案: 【解析】本节课主要学习了矩形的定义、性质,要求我们
1.弄清矩形的性质与平行四边形性质的区别与联系.
2.会应用矩形的性质证明一些几何问题.人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定、冷静,学习如何从慌乱中找到生机。
——席慕蓉
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
