湘教版八下数学2.7正方形教学课件(32张PPT)
文档属性
| 名称 | 湘教版八下数学2.7正方形教学课件(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 09:15:03 | ||
图片预览




文档简介
课件32张PPT。2.7 正方形1.掌握正方形的定义、性质和判定,并会用它们进行有关的证明和计算.
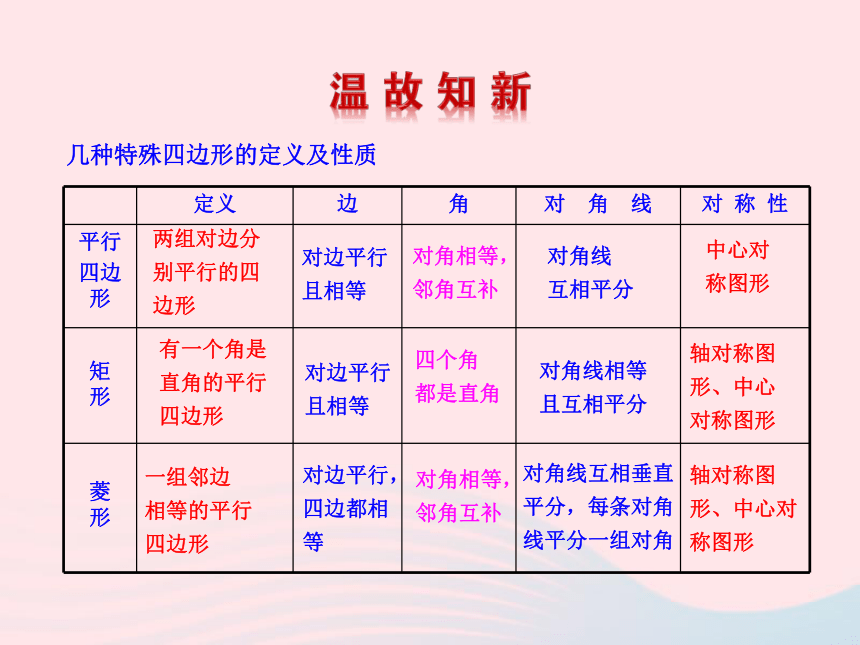
2.理解正方形与平行四边形、矩形、菱形的联系和区别.几种特殊四边形的定义及性质 对边平行
且相等对边平行且相等对边平行,四边都相等对角相等,
邻角互补四个角
都是直角对角相等,邻角互补对角线
互相平分对角线相等
且互相平分对角线互相垂直平分,每条对角线平分一组对角中心对
称图形轴对称图形、中心对称图形轴对称图
形、中心对称图形两组对边分
别平行的四
边形有一个角是
直角的平行
四边形一组邻边
相等的平行
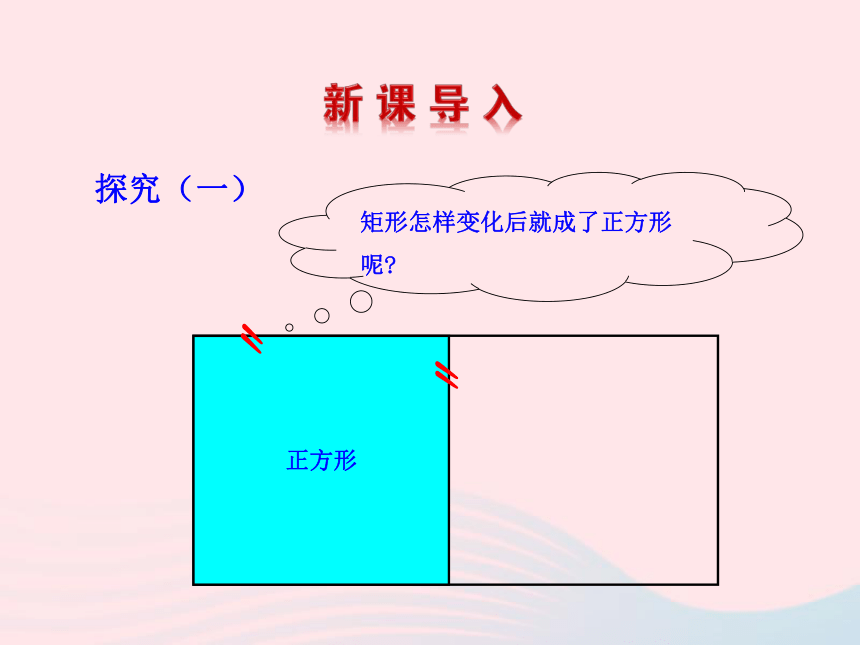
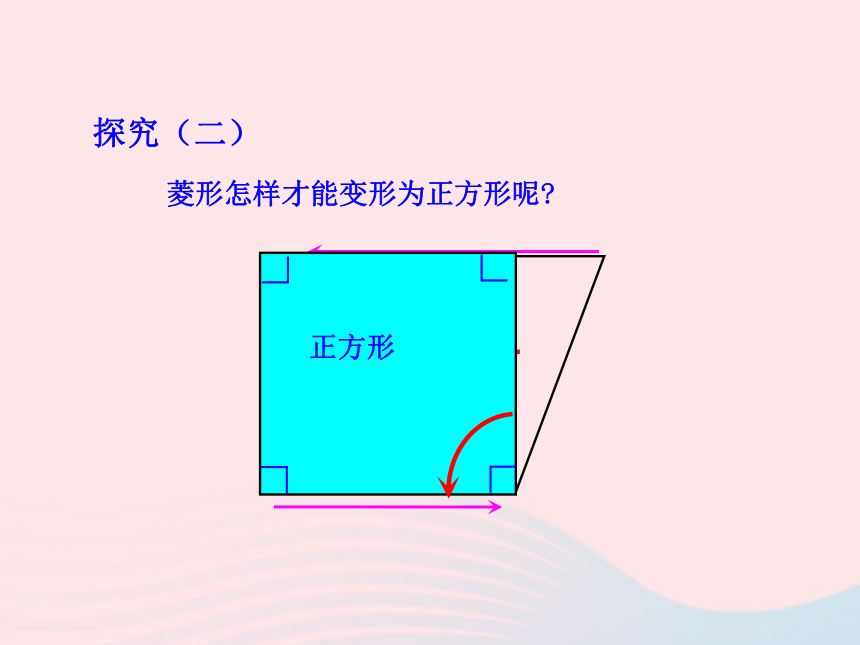
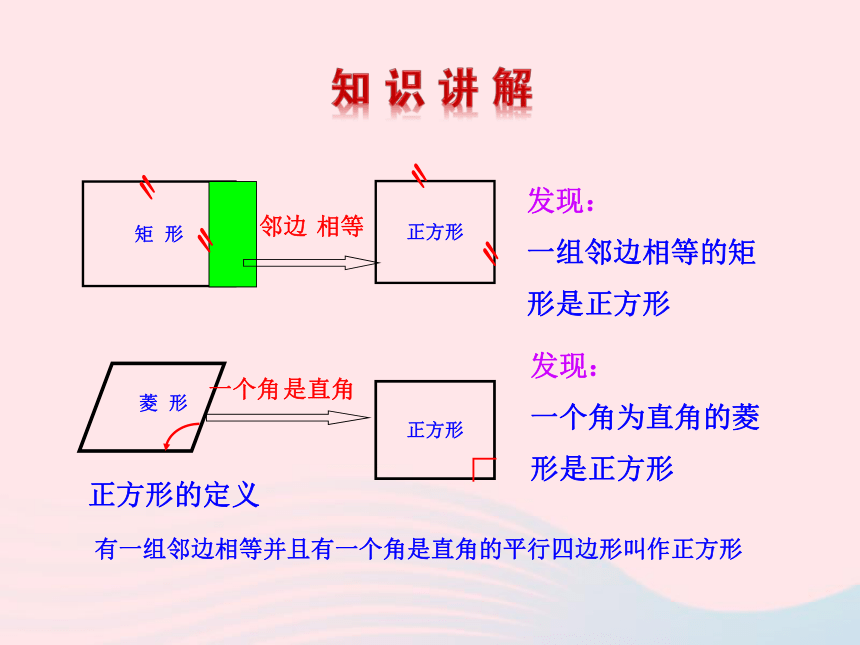
四边形矩形正方形〃〃矩形怎样变化后就成了正方形呢?探究(一)∟∟∟∟正方形菱形怎样才能变形为正方形呢?探究(二)矩 形〃〃正方形邻边相等〃〃发现:
一组邻边相等的矩形是正方形一个角是直角正方形∟发现:
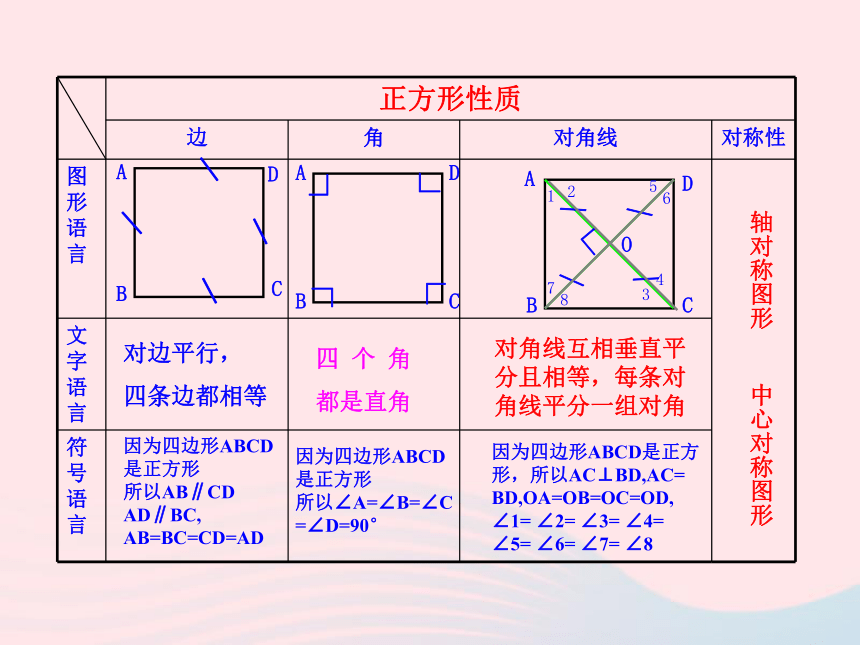
一个角为直角的菱形是正方形正方形的定义有一组邻边相等并且有一个角是直角的平行四边形叫作正方形ACDBACDBACDB\∟∟∟∟O\\∟对边平行, 四条边都相等 四 个 角
都是直角对角线互相垂直平分且相等,每条对角线平分一组对角因为四边形ABCD是正方形
所以AB∥CD AD∥BC, AB=BC=CD=AD因为四边形ABCD是正方形
所以∠A=∠B=∠C
=∠D=90°因为四边形ABCD是正方
形,所以AC⊥BD,AC=
BD,OA=OB=OC=OD,
∠1= ∠2= ∠3= ∠4=
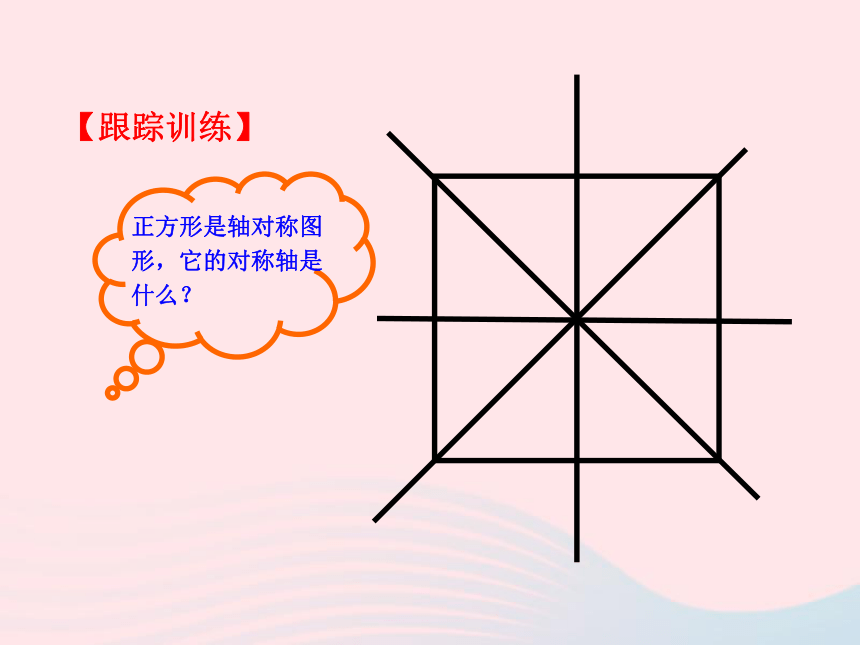
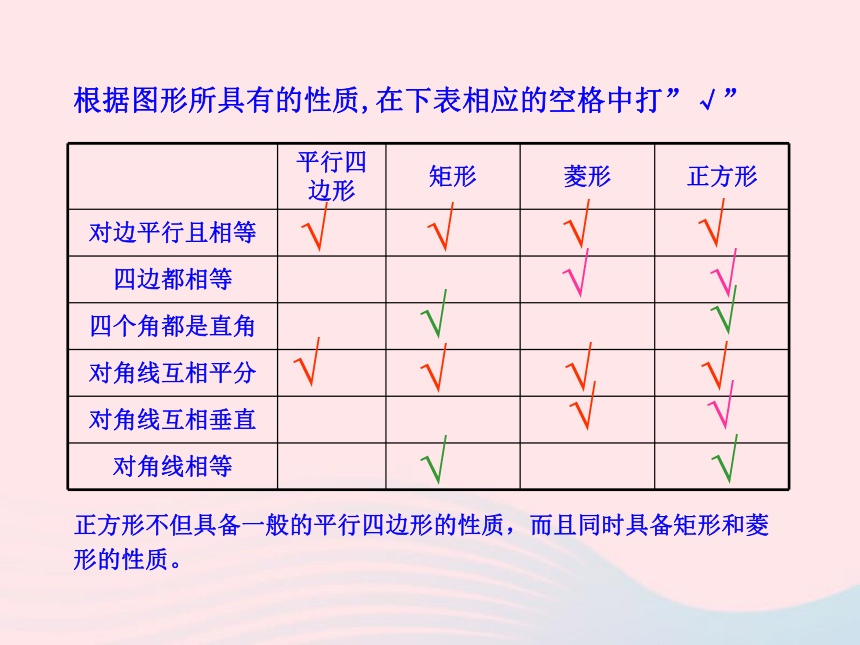
∠5= ∠6= ∠7= ∠8轴对称图形 中心对称图形12345678【跟踪训练】根据图形所具有的性质,在下表相应的空格中打”√”√√√√√√√√√√√√√√正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。√√求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.例1 已知:如图,四边形ABCD是正方形,对
角线AC、BD相交于点O,证明:因为四边形ABCD是正方形,所以AC=BD,AC⊥BD,AO=BO=CO=DO.所以△ABO、△BCO、△CDO、【例题】例2:AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:EC=EF=FB证明:因为 四边形ABCD是正方形
所以∠B=90°,∠ACB=45°,
因为∠AEF=∠B =90°,AB=AE,AF=AF,
所以△ABF≌△AEF(HL),
所以BF=EF,
又因为∠FEC=90° 所以∠EFC=45°,
所以EC=EF(等角对等边),
所以BF=EF=EC . 【例题】(红河·中考)如图,在正方形ABCD中,G是BC上的任意一点(G与B、C两点不重合),E、F是AG上的两点(E、F与A、G两点不重合),若AF=BF+EF,∠1=∠2,
请判断线段DE与BF有怎样的位置关系,并证明你的结论.【跟踪训练】【解析】根据题目条件可判断DE∥BF.
证明如下:
因为四边形ABCD是正方形,
所以AB=AD,
因为AF=AE+EF,又AF=BF+EF,
所以AE=BF,
因为∠1=∠2,所以△ABF≌△DAE(SAS).
所以∠AFB=∠DEA,∠BAF=∠ADE.
因为∠BAF+∠2=90°,
所以∠ADE+∠2=90°,所以 ∠BAF+ ∠1=90°
所以∠AED=∠BFA=90°,
所以DE∥BF.一组邻边相等有一个内角是直角一组邻边相等有一个内角是直角正方形的判定一组邻边相等且
有一个角是直角ABCDEFGH123例3 已知:正方形ABCD中,点E,F,G,H分别在AB,BC,CD,DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?并证明你的结论.【例题】证明:四边形EFGH是正方形,
因为四边形ABCD是正方形,
所以∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=AD=DC=BC.
又因为AE=BF=CG=DH,
所以AB-AE=AD-DH=DC-CG=BC-BF,
即BE=AH=DG=CF,
所以△AEH≌△BFE≌ △CGF ≌ △DHG.所以EH=HG=FG=EF,
因为∠1=∠3.又∠3+∠2=90°所以∠1+∠2=90°.
所以四边形EFGH是正方形.1.ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?ADBCE【解析】连接AC.因为四边形ABCD是正方形所以∠B=90°,AB=BC因为EC=50m,EB=30m所以 S正方形ABCD=(40 m)2=1600(m2)所以 所以 【跟踪训练】2.在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?解析:有无数方法,只要两直线垂直且交点在正方形的对角线交点处即可.平行四边形矩形菱形正
方
形3.你能用恰当的方式表示出平行四边形、矩形、菱形、正方形之间的包含关系吗?解析:1.(义乌·中考)下列说法不正确的是( )
(A)一组邻边相等的矩形是正方形
(B)对角线相等的菱形是正方形
(C)对角线互相垂直的矩形是正方形
(D)有一个角是直角的平行四边形是正方形
【解析】选D.有一个角是直角的平行四边形可能是矩形,也可能是正方形.2.(苏州·中考)如图,四边形
ABCD是正方形,延长AB到E,使AE=AC,
则∠BCE的度数是_______°.
【解析】因为四边形ABCD是正方形,
所以∠CAE=45°,∠ABC=90°,
又因为AE=AC,所以∠E=∠ACE=67.5°,
所以∠BCE=90°-∠E=90°-67.5°=22.5°.
答案:22.53.(宜宾·中考)如图,点P是正方形ABCD的对角线
BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出
下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等
腰三角形;④∠PFE=∠BAP;⑤PD= EC.其中正确结
论的序号是_____.【解析】延长FP交AB于点G,延长AP交EF于点H,交EC于点M,由题意易证,△BPE、△DPF为等腰直角三角形,四边形PECF为矩形,四边形BEPG为正方形.
易证△APG≌△FEP,
所以AP=EF,∠BAP=∠PFE,又PE∥FC,
所以∠PFE=∠FEC=∠BAP,
又∠BAP+∠BMA=90°,所以∠FEM+∠BMA=90°,
所以∠EHM=90°即AP⊥EF.
在等腰直角三角形PDF中,
PD= PF= EC.
答案:①②④⑤4.如图,正方形ABCD和正方形OEFG的边
长均为4,O是正方形ABCD的旋转对称中
心,则图中阴影部分的面积是______.
【解析】连接OC,OD.易证图中阴影部分
的面积等于△COD的面积,即正方形面积
的四分之一,故阴影部分面积为4.
答案:45.(滨州·中考)如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
(1)请判断四边形EFGH的形状?并说明为什么.
(2)要使四边形EFGH为正方形,那么四边形ABCD的对角线应该有怎样的情况?【解析】(1)四边形EFGH是平行四边形.
连接AC,
因为E、F分别是AB、BC的中点
所以EF∥AC,EF= AC
同理HG∥AC,HG= AC
所以EF HG,
所以四边形EFGH是平行四边形.
(2)四边形ABCD的对角线互相垂直且相等.通过本课时的学习,需要我们
1.掌握正方形的定义、性质、判定.
2.了解正方形、矩形、菱形、平行四边形间的关系,认识它们之间的联系和区别.
3.能综合利用正方形的性质与判定解决有关的证明与计算.一、正方形的定义:直角相等平行且相等相等垂直平分一组对角中心轴4菱形矩形矩形菱形相等直角天将降大任于斯人也,必先苦其心志,劳其筋 骨,饿其体肤,空乏其身,行拂乱其所为。
——《孟子?告子下》
2.理解正方形与平行四边形、矩形、菱形的联系和区别.几种特殊四边形的定义及性质 对边平行
且相等对边平行且相等对边平行,四边都相等对角相等,
邻角互补四个角
都是直角对角相等,邻角互补对角线
互相平分对角线相等
且互相平分对角线互相垂直平分,每条对角线平分一组对角中心对
称图形轴对称图形、中心对称图形轴对称图
形、中心对称图形两组对边分
别平行的四
边形有一个角是
直角的平行
四边形一组邻边
相等的平行
四边形矩形正方形〃〃矩形怎样变化后就成了正方形呢?探究(一)∟∟∟∟正方形菱形怎样才能变形为正方形呢?探究(二)矩 形〃〃正方形邻边相等〃〃发现:
一组邻边相等的矩形是正方形一个角是直角正方形∟发现:
一个角为直角的菱形是正方形正方形的定义有一组邻边相等并且有一个角是直角的平行四边形叫作正方形ACDBACDBACDB\∟∟∟∟O\\∟对边平行, 四条边都相等 四 个 角
都是直角对角线互相垂直平分且相等,每条对角线平分一组对角因为四边形ABCD是正方形
所以AB∥CD AD∥BC, AB=BC=CD=AD因为四边形ABCD是正方形
所以∠A=∠B=∠C
=∠D=90°因为四边形ABCD是正方
形,所以AC⊥BD,AC=
BD,OA=OB=OC=OD,
∠1= ∠2= ∠3= ∠4=
∠5= ∠6= ∠7= ∠8轴对称图形 中心对称图形12345678【跟踪训练】根据图形所具有的性质,在下表相应的空格中打”√”√√√√√√√√√√√√√√正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。√√求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.例1 已知:如图,四边形ABCD是正方形,对
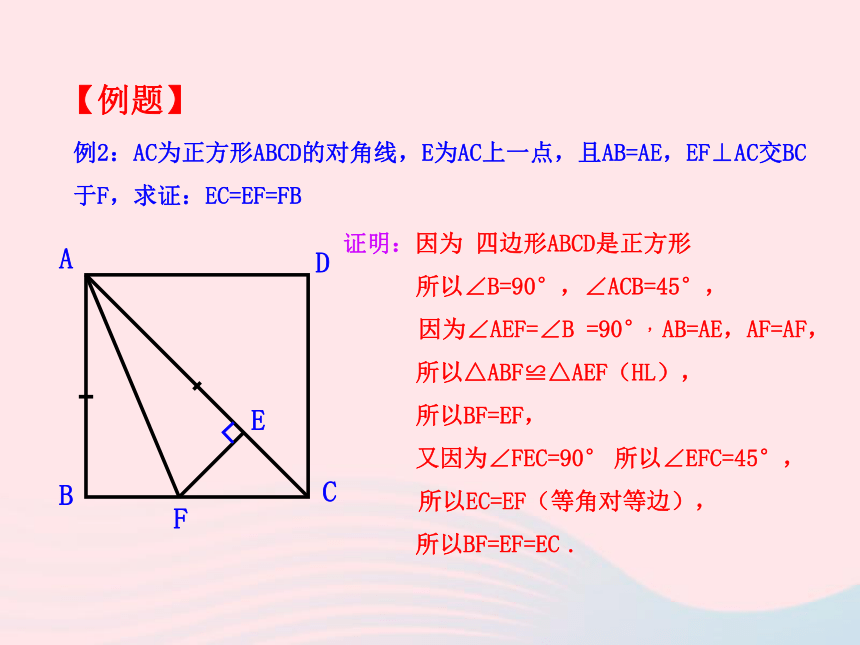
角线AC、BD相交于点O,证明:因为四边形ABCD是正方形,所以AC=BD,AC⊥BD,AO=BO=CO=DO.所以△ABO、△BCO、△CDO、【例题】例2:AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:EC=EF=FB证明:因为 四边形ABCD是正方形
所以∠B=90°,∠ACB=45°,
因为∠AEF=∠B =90°,AB=AE,AF=AF,
所以△ABF≌△AEF(HL),
所以BF=EF,
又因为∠FEC=90° 所以∠EFC=45°,
所以EC=EF(等角对等边),
所以BF=EF=EC . 【例题】(红河·中考)如图,在正方形ABCD中,G是BC上的任意一点(G与B、C两点不重合),E、F是AG上的两点(E、F与A、G两点不重合),若AF=BF+EF,∠1=∠2,
请判断线段DE与BF有怎样的位置关系,并证明你的结论.【跟踪训练】【解析】根据题目条件可判断DE∥BF.
证明如下:
因为四边形ABCD是正方形,
所以AB=AD,
因为AF=AE+EF,又AF=BF+EF,
所以AE=BF,
因为∠1=∠2,所以△ABF≌△DAE(SAS).
所以∠AFB=∠DEA,∠BAF=∠ADE.
因为∠BAF+∠2=90°,
所以∠ADE+∠2=90°,所以 ∠BAF+ ∠1=90°
所以∠AED=∠BFA=90°,
所以DE∥BF.一组邻边相等有一个内角是直角一组邻边相等有一个内角是直角正方形的判定一组邻边相等且
有一个角是直角ABCDEFGH123例3 已知:正方形ABCD中,点E,F,G,H分别在AB,BC,CD,DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?并证明你的结论.【例题】证明:四边形EFGH是正方形,
因为四边形ABCD是正方形,
所以∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=AD=DC=BC.
又因为AE=BF=CG=DH,
所以AB-AE=AD-DH=DC-CG=BC-BF,
即BE=AH=DG=CF,
所以△AEH≌△BFE≌ △CGF ≌ △DHG.所以EH=HG=FG=EF,
因为∠1=∠3.又∠3+∠2=90°所以∠1+∠2=90°.
所以四边形EFGH是正方形.1.ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?ADBCE【解析】连接AC.因为四边形ABCD是正方形所以∠B=90°,AB=BC因为EC=50m,EB=30m所以 S正方形ABCD=(40 m)2=1600(m2)所以 所以 【跟踪训练】2.在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?解析:有无数方法,只要两直线垂直且交点在正方形的对角线交点处即可.平行四边形矩形菱形正
方
形3.你能用恰当的方式表示出平行四边形、矩形、菱形、正方形之间的包含关系吗?解析:1.(义乌·中考)下列说法不正确的是( )
(A)一组邻边相等的矩形是正方形
(B)对角线相等的菱形是正方形
(C)对角线互相垂直的矩形是正方形
(D)有一个角是直角的平行四边形是正方形
【解析】选D.有一个角是直角的平行四边形可能是矩形,也可能是正方形.2.(苏州·中考)如图,四边形
ABCD是正方形,延长AB到E,使AE=AC,
则∠BCE的度数是_______°.
【解析】因为四边形ABCD是正方形,
所以∠CAE=45°,∠ABC=90°,
又因为AE=AC,所以∠E=∠ACE=67.5°,
所以∠BCE=90°-∠E=90°-67.5°=22.5°.
答案:22.53.(宜宾·中考)如图,点P是正方形ABCD的对角线
BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出
下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等
腰三角形;④∠PFE=∠BAP;⑤PD= EC.其中正确结
论的序号是_____.【解析】延长FP交AB于点G,延长AP交EF于点H,交EC于点M,由题意易证,△BPE、△DPF为等腰直角三角形,四边形PECF为矩形,四边形BEPG为正方形.
易证△APG≌△FEP,
所以AP=EF,∠BAP=∠PFE,又PE∥FC,
所以∠PFE=∠FEC=∠BAP,
又∠BAP+∠BMA=90°,所以∠FEM+∠BMA=90°,
所以∠EHM=90°即AP⊥EF.
在等腰直角三角形PDF中,
PD= PF= EC.
答案:①②④⑤4.如图,正方形ABCD和正方形OEFG的边
长均为4,O是正方形ABCD的旋转对称中
心,则图中阴影部分的面积是______.
【解析】连接OC,OD.易证图中阴影部分
的面积等于△COD的面积,即正方形面积
的四分之一,故阴影部分面积为4.
答案:45.(滨州·中考)如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
(1)请判断四边形EFGH的形状?并说明为什么.
(2)要使四边形EFGH为正方形,那么四边形ABCD的对角线应该有怎样的情况?【解析】(1)四边形EFGH是平行四边形.
连接AC,
因为E、F分别是AB、BC的中点
所以EF∥AC,EF= AC
同理HG∥AC,HG= AC
所以EF HG,
所以四边形EFGH是平行四边形.
(2)四边形ABCD的对角线互相垂直且相等.通过本课时的学习,需要我们
1.掌握正方形的定义、性质、判定.
2.了解正方形、矩形、菱形、平行四边形间的关系,认识它们之间的联系和区别.
3.能综合利用正方形的性质与判定解决有关的证明与计算.一、正方形的定义:直角相等平行且相等相等垂直平分一组对角中心轴4菱形矩形矩形菱形相等直角天将降大任于斯人也,必先苦其心志,劳其筋 骨,饿其体肤,空乏其身,行拂乱其所为。
——《孟子?告子下》
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
