沪科版数学八年级下册第19章《四边形》单元测试卷 (含详细答案)
文档属性
| 名称 | 沪科版数学八年级下册第19章《四边形》单元测试卷 (含详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 313.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 13:26:50 | ||
图片预览




文档简介
沪科新版八年级下册第19章《四边形》单元测试卷
满分100分
班级:________姓名:________学号:________成绩:________
一.选择题(共8小题,,满分24分)
1.从五边形的一个顶点出发可以连接的对角线条数为( )
A.1 B.2 C.3 D.4
2.内角和为540°的多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
3.下列边长相等的正多边形能完成镶嵌的是( )
A.2个正八边形和1个正三角形
B.3个正方形和2个正三角形
C.1个正五边形和1个正十边形
D.2个正六边形和2个正三角形
4.如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是( )
A.9m B.12m C.8m D.10m
5.下列判断错误的是( )
A.两组对角分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.一组对边平行且对角线相等的四边形是矩形
D.四条边都相等的四边形是菱形
6.如图,在四边形ABCD中,对角线AC,BD相交于点O,添加下列条件后仍不能判定四边形ABCD是平行四边形的是( )
A.AD∥BC,AO=CO B.AD=BC,AO=OC
C.AD=BC,CD=AB D.S△AOD=S△COD=S△BOC
7.如图,在正方形ABCD内,以BC为边作等边三角形BCM,连接AM并延长交CD于N,则下列结论不正确的是( )
A.∠DAN=15° B.∠CMN=45° C.AM=MN D.MN=NC
8.若一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为( )
A.14或15 B.13或14 C.13或14或15 D.14或15或16
二.填空题(共8小题,满分24分)
9.正七边形的外角和是 .
10.如图,在平行四边形ABCD中,∠A与∠B的度数之比为2:1,则∠A= °.
11.如图,五边形ABCDE的对角线共有 条.
12.如图,菱形ABCD中,∠ABC=130°,DE⊥AB于点E,则∠BDE= °.
13.如图,在矩形ABCD中,AC,BD交于点O,M、N分别为BC、OC的中点.若BD=8,则MN的长为 .
14.如图,在菱形ABCD中,连接BD,点E在AB上,连接CE交BD于点F,作FG⊥BC于点G,∠BEC=3∠BCE,BF=DF,若FG=,则AB的长为 .
15.阅读:将一个量用两种方法分别计算一次,由结果相同构造等式解决问题,这种思维方法称为“算两次”原理,又称“富比尼原理”,比如我们常用的等积法是其中的一种.如图,在长方形ABCD中,AB=4cm,BC=3cm,E是CD的中点,动点P从点A出发,以每秒1cm的速度沿点A→B→C→E运动,最终到达点E.若点P运动的时间为ts,则当t= s时,S△APE=4.
16.如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…以此类推,则第2020个三角形的周长是 .
三.解答题(共7小题,满分52分)
17.矩形ABCD中,AE平分∠BAD交BC于点E,CF平分∠BCD交AD于点F,求证:AE∥CF.
18.如图,在?ABCD中,点E是BC上的一点,连接DE,在DE上取一点F使得∠AFE=∠ADC.若DE=AD,求证:DF=CE.
19.已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC、DE,当∠B=∠AEB=45°时,求证四边形ACED是正方形.
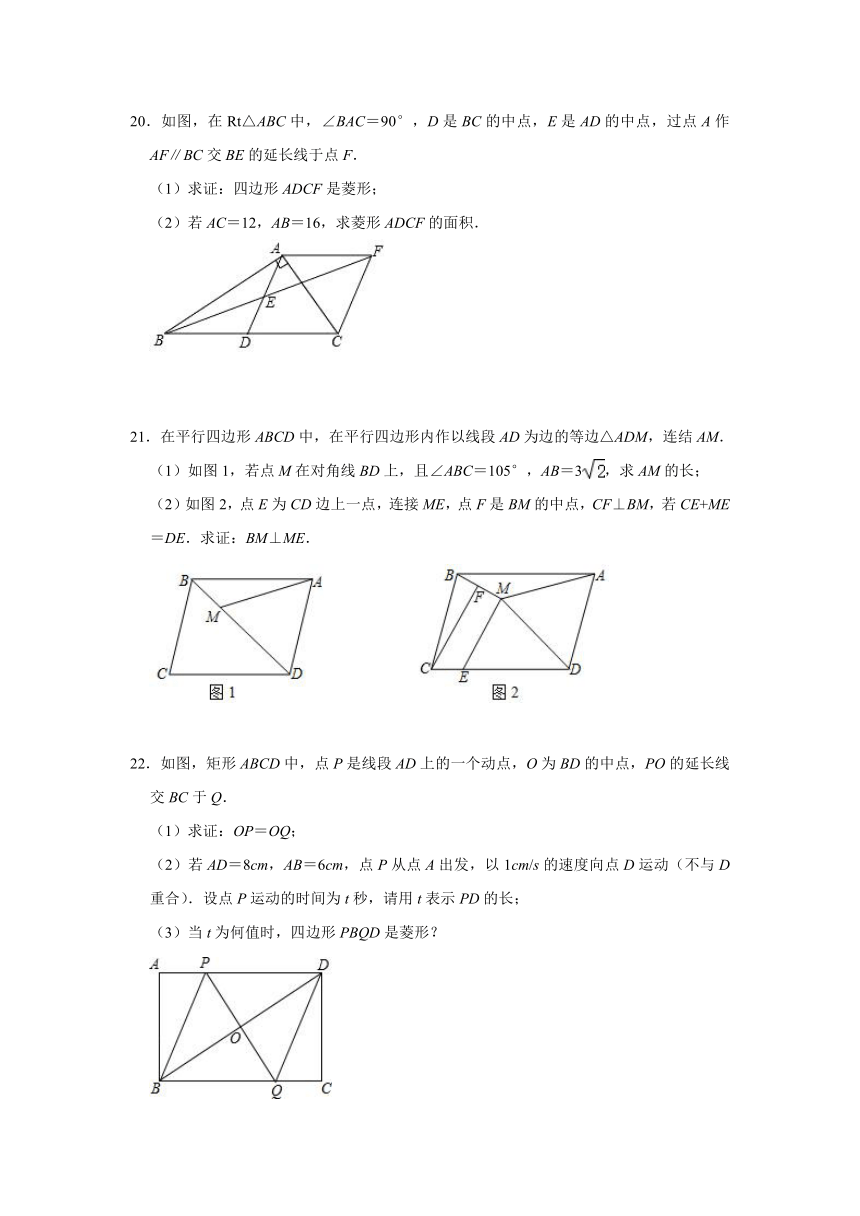
20.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若AC=12,AB=16,求菱形ADCF的面积.
21.在平行四边形ABCD中,在平行四边形内作以线段AD为边的等边△ADM,连结AM.
(1)如图1,若点M在对角线BD上,且∠ABC=105°,AB=3,求AM的长;
(2)如图2,点E为CD边上一点,连接ME,点F是BM的中点,CF⊥BM,若CE+ME=DE.求证:BM⊥ME.
22.如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
23.如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F,
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
参考答案
一.选择题(共8小题)
1.【解答】解:∵n边形(n>3)从一个顶点出发可以引(n﹣3)条对角线,
∴从五边形的一个顶点出发可以画出5﹣3=2(条)对角线.
故选:B.
2.【解答】解:设这个多边形的边数是n,
则(n﹣2)?180°=540°,
解得n=5,
故选:C.
3.【解答】解:A、正三角形的每个内角是60°,正八边形形的每个内角是135°,∵2×135°+1×90°≠360°,不能密铺.
B、正三角形的每个内角是60°,正方形的每个内角是90°,∵3×90°+2×60°≠360°,不能密铺.
C、正五边形的每个内角是108°,正十边形的每个内角是144°,∵108°+144°≠360°,不能密铺.
D、正六边形的每个内角是120°,正三角形每个内角是60°,2×120°+2×60°=360°,能铺满.
故选:D.
4.【解答】解:∵A、B分别是CD、CE的中点,若DE=18m,
∴AB=DE=9m,
故选:A.
5.【解答】解:A、两组对角分别相等的四边形是平行四边形,故A选项不符合题意;
B、四个内角都相等的四边形是矩形,故B选项不符合题意;
C、一组对边平行且对角线相等的四边形不一定是矩形,故C选项符合题意;
D、四条边都相等的四边形是菱形,故D选项不符合题意;
故选:C.
6.【解答】解:若∵AD∥BC,
∴∠ADO=∠CBO,且AO=CO,∠AOD=∠BOC,
∴△AOD≌△COB(AAS)
∴AD=BC,
∴四边形ABCD是平行四边形,故A选项不合题意;
若AD=BC,CD=AB,
∴四边形ABCD是平行四边形,故C选项不合题意;
若S△AOD=S△COD=S△BOC,
∴AO=CO,BO=DO,
∴四边形ABCD是平行四边形,故D选项不合题意;
故选:B.
7.【解答】解:作MG⊥BC于G.
∵四边形ABCD是正方形,
∴BA=BC,∠ABC=∠DAB=°∠DCB=90°
∵△MBC是等边三角形,
∴MB=MC=BC,∠MBC=∠BMC=60°,
∵MG⊥BC,
∴BG=GC,
∵AB∥MG∥CD,
∴AM=MN,
∴∠ABM=30°,
∵BA=BM,
∴∠MAB=∠BMA=75°,
∴∠DAN=90°﹣75°=15°,∠CMN=180°﹣75°﹣60°=45°,
故A,B,C正确,
故选:D.
8.【解答】解:如图,n边形,A1A2A3…An,
若沿着直线A1A3截去一个角,所得到的多边形,比原来的多边形的边数少1,
若沿着直线A1M截去一个角,所得到的多边形,与原来的多边形的边数相等,
若沿着直线A1N截去一个角,所得到的多边形,比原来的多边形的边数多1,
因此将一个多边形截去一个角后,变成十四边形,则原来的四边形为13或14或15,
故选:C.
二.填空题(共8小题)
9.【解答】解:根据任意多边形的外角和都为360°,可知正七边形的外角和是360°,
故答案为360°.
10.【解答】解:∵四边形ABCD为平行四边形,
∴∠A+∠B=180°,
∵∠A:∠B=2:1,
∴∠A=×180°=120°.
故答案为:120.
11.【解答】解:五边形ABCDE的对角线共有=5(条).
故答案为:5.
12.【解答】解:∵四边形ABCD是菱形,
∴∠DBC=∠DBA=∠ABC=65°,
∵DE⊥AB,
∴∠DBE+∠BDE=90°,
∴∠BDE=25°,
故答案为:25.
13.【解答】解:如图,∵四边形ABCD是矩形,AC,BD交于点O,BD=8
∴BD=2BO,即2BO=8.
∴BO=4.
又∵M、N分别为BC、OC的中点,
∴MN是△CBO的中位线,
∴MN=BO=2.
故答案是:2.
14.【解答】解:连接AC交BD于M,如图所示:
设BF=5a,则DF=11a,
∴BD=16a,
∵四边形ABCD是菱形,
∴AC⊥BD,∠ACB=∠ACD,AB=BC,AB∥CD,BM=DM=BD=8a,
∴FM=BM﹣BF=3a,
∵AB∥CD,
∴∠BEC=∠ECD,
∵∠BEC=3∠BCE,
∴∠ECD=3∠BCE,
∴∠ACE=∠BCE,
∴CF平分∠ACB,
∵FG⊥BC,FM⊥AC,
∴FG=FM=,
∴3a=,
∴a=,
∴BF=,BM=2,
在Rt△FMC和Rt△FGC中,,
∴Rt△FMC≌Rt△FGC(HL),
∴CG=CM,
在Rt△BFG中,BG===1,
设CG=CM=x,则BC=x+1,
在Rt△BMC中,由勾股定理得:22+x2=(x+1)2,
解得:x=,
∴AB=BC=.
15.【解答】解:①如图1,
当P在AB上时,
∵△APE的面积等于4,
∴t?3=4,
t=;
②当P在BC上时,如图2,
∵△APE的面积等于4,
∴S长方形ABCD﹣S△CPE﹣S△ADE﹣S△ABP=4,
∴3×4﹣(3+4﹣t)×2﹣×2×3﹣×4×(t﹣4)=4,
t=6;
③当P在CE上时,如图3,
∴(4+3+2﹣t)×3=4,
t=<3+4,此时不符合;
故答案为:或6.
16.【解答】解:∵△A1B1C1中,A1B1=4,A1C1=5,B1C1=7,
∴△A1B1C1的周长是16,
∵A2,B2,C2分别是边B1C1,A1C1,A1B1的中点,
∴B2C2,A2C2,A2B2分别等于A1B1、B1C1、C1A1的,
…,
以此类推,则△A4B4C4的周长是×16,
∴△AnBn?n的周长是,
则第2020个三角形的周长是=.
故答案为:.
三.解答题(共7小题)
17.【解答】证明:∵四边形ABCD是矩形,
∴AD∥BC,∠BAD=∠BCD=90°,
∴∠AEB=∠DAE,
∵AE平分∠BAD,CF平分∠BCD,
∴∠DAE=∠BAD=45°,∠BCF=∠BCD=45°,
∴∠AEB=∠DAE=∠BCF,
∴AE∥CF.
18.【解答】证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC,
∵∠AFD+∠AFE=180°,∠AFE=∠ADC,
∴∠AFD=∠C,
在△AFD和△DEC中,,
∴△AFD≌△DCE(AAS),
∴DF=CE.
19.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
∵O是CD的中点,
∴OC=OD,
在△AOD和△EOC中,,
∴△AOD≌△EOC(AAS);
(2)∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,
∴AB=AE,∠BAE=90°
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.
∴?ACED是菱形.
∵AB=AE,AB=CD,
∴AE=CD.
∴菱形ACED是正方形.
20.【解答】(1)证明:∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
∵,
∴△AEF≌△DEB(AAS),
∴AF=DB,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=CD=BC,
∴四边形ADCF是菱形;
(2)解:设AF到CD的距离为h,
∵AF∥BC,AF=BD=CD,∠BAC=90°,
∴S菱形ADCF=CD?h=BC?h=S△ABC=AB?AC=×12×16=96.
21.【解答】解:(1)如图1,过点C作CN⊥BD于N,
∵四边形ABCD是平行四边形,
∴BC=AD,AB=CD=3,∠ABC=∠ADC=105°,AD∥BC,
∴∠CBD=∠ADB,
∵△ADM是等边三角形,
∴AD=AM=MD,∠ADM=60°,
∴∠CBD=60°,∠CDN=45°,
∵CN⊥BD,
∴∠BCN=30°,∠NCD=∠NDC=45°,
∴CN=DN,CD=CN=3,
∴CN=3,
∵∠BCN=30°,CN⊥BD,
∴CN=BN,BC=2BN,
∴BN=,BC=2,
∴BC=AD=AM=2;
(2)在ED上截取EH=EM,连接CM,MH,
∵点F是BM的中点,CF⊥BM,
∴CM=BC,且CF⊥BM,
∴∠BCF=∠MCF,
∴CM=BC=MD=AD,
∴∠MCD=∠MDC,
∵CE+ME=DE,DE=EH+DH,且ME=EH,
∴CE=DH,且∠MCD=∠MDC,CM=DM,
∴△MCE≌△MDH(SAS)
∴MH=ME,
∴MH=ME=EH,
∴△MEH是等边三角形,
∴∠MEH=60°,
∵AD∥BC,
∴∠BCD+∠ADC=180°,
∴∠BCF+∠FCM+∠MCD+∠MDC+60°=180°,
∴2∠FCM+2∠MCD=120°,
∴∠FCD=60°=∠MEH,
∴CF∥ME,且CF⊥BM,
∴BM⊥ME.
22.【解答】解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
∵O为BD的中点,
∴DO=BO,
在△PDO和△QBO中,
,
∴△PDO≌△QBO(ASA),
∴OP=OQ;
(2)由题意知:AD=8cm,AP=tcm,
∴PD=8﹣t,
(3)∵PB=PD,
∴PB2=PD2,
即AB2+AP2=PD2,
∴62+t2=(8﹣t)2,
解得 t=,
∴当t=时,PB=PD.
23.【解答】(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)解:由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPE=∠EDF=90°
(3)解:AP=CE;理由如下:
在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
