人教版高中数学2019-2020 选修二 2-3 第二章 2.4 正态分布 课件(共21张PPT)
文档属性
| 名称 | 人教版高中数学2019-2020 选修二 2-3 第二章 2.4 正态分布 课件(共21张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 777.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 10:26:05 | ||
图片预览






文档简介
(共21张PPT)
100个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
温故知新:
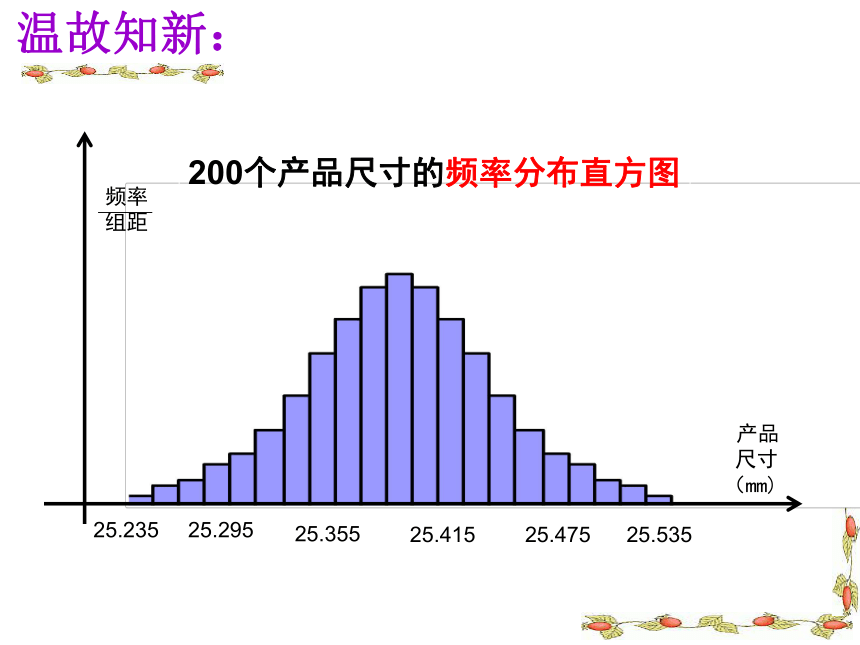
200个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
温故知新:
频率
组距
产品
尺寸
(mm)
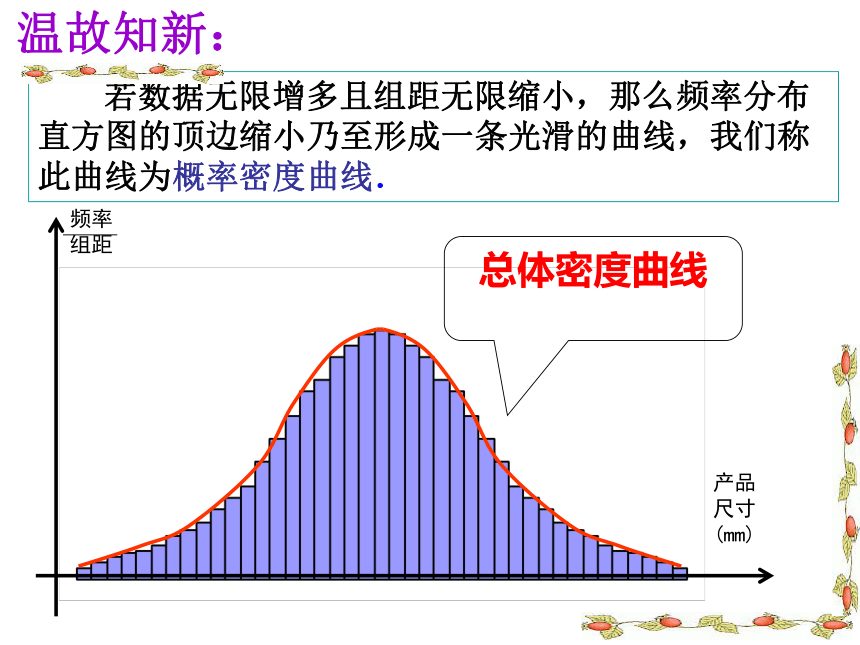
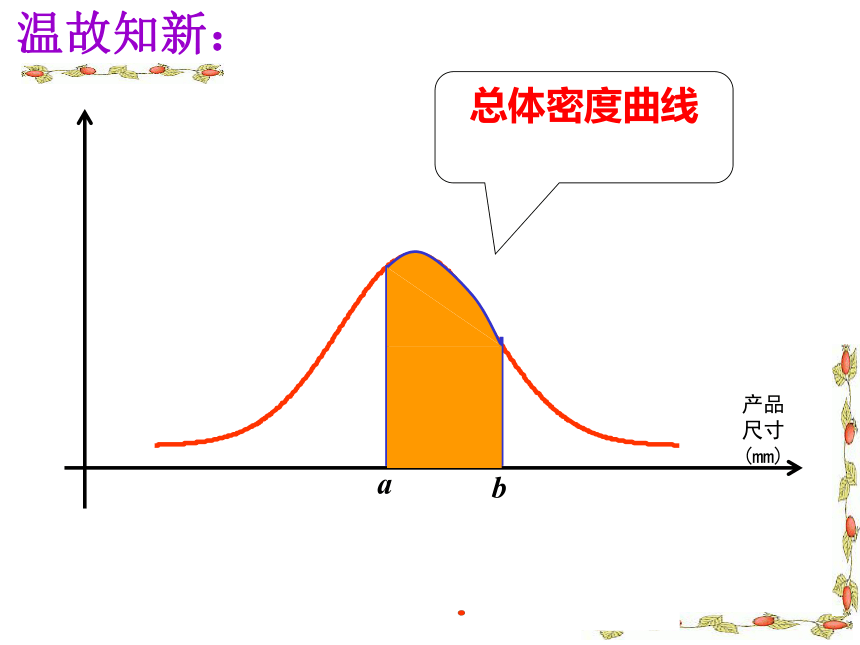
总体密度曲线
若数据无限增多且组距无限缩小,那么频率分布直方图的顶边缩小乃至形成一条光滑的曲线,我们称此曲线为概率密度曲线.
温故知新:
产品
尺寸
(mm)
总体密度曲线
温故知新:
产品尺寸的总体密度曲线就是或近似地是以下函数的图象:
这个总体的分布叫做正态分布(normal distribution)
其中式中的实数μ、σ(σ>0)是参数,分别表示总体的平均数与标准差。正态分布完全由μ、σ确定,因此常记作:
正态分布:
正态函数
正态分布是应用最广泛的一种连续型分布.
正态分布在十九世纪前叶由高斯加以推广,所以通常称为高斯分布.
德莫佛最早发现了二项概率的一个近似公式,这一公式被认为是正态分布的首次露面.
正态分布:
(1)在生产中,各种产品的质量指标一般都服从正态分布;
(2)在测量中,测量结果、测量的随机误差都服从正态分布;
(3)在生物学中,同一群体的某种特征都服从正态分布;
(4)在气象中,某地每年七月份的平均气温、平均湿度、降雨量等都服从正态分布。
正态分布的意义:
m 的意义
产品
尺寸
(mm)
总体平均数反映总体随机变量的
平均水平
x3
x4
x= μ
总体标准差反映总体随机变量的
集中与分散的程度
s的意义
给出下列三个正态密度曲线的函数表达式,请找出其均值μ和标准差σ。
(1)
(2)
( 3 )
0,1
1,2
-1,0.5
例题1:
1.下列函数是正态密度函数的是( ).
B
C
牛刀小试:
m
曲线函数:
两头低、中间高、左右对称
曲线性质:
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(4)曲线与x轴之间的面积为1
曲线性质:
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
曲线性质:
m-a
m+a
x=μ
知识小结:
内取值的概率。
区间
取值概率
68.26%
95.44%
99.74%
小概率事件
(μ-σ,μ+σ)
(μ-2σ,μ+2σ)
(μ-3σ,μ+3σ)
设一次数学考试中满分为150分,某班学生的分数服从正态分布N(110,202),如果这个班有54人,估计这个班的及格人数(不小于90分)和130分以上的人数
例题2
有一种精密零件,其尺寸X(单位mm)服从N(20,4)。若这批零件共有5000个,试求:
(1)尺寸在18mm~22mm间的零件的百分比;
(2)若尺寸在24mm~26mm间的零件为不合格,则不合格的零件大约有多少个?
例题3
100个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
温故知新:
200个产品尺寸的频率分布直方图
25.235
25.295
25.355
25.415
25.475
25.535
产品
尺寸
(mm)
频率
组距
温故知新:
频率
组距
产品
尺寸
(mm)
总体密度曲线
若数据无限增多且组距无限缩小,那么频率分布直方图的顶边缩小乃至形成一条光滑的曲线,我们称此曲线为概率密度曲线.
温故知新:
产品
尺寸
(mm)
总体密度曲线
温故知新:
产品尺寸的总体密度曲线就是或近似地是以下函数的图象:
这个总体的分布叫做正态分布(normal distribution)
其中式中的实数μ、σ(σ>0)是参数,分别表示总体的平均数与标准差。正态分布完全由μ、σ确定,因此常记作:
正态分布:
正态函数
正态分布是应用最广泛的一种连续型分布.
正态分布在十九世纪前叶由高斯加以推广,所以通常称为高斯分布.
德莫佛最早发现了二项概率的一个近似公式,这一公式被认为是正态分布的首次露面.
正态分布:
(1)在生产中,各种产品的质量指标一般都服从正态分布;
(2)在测量中,测量结果、测量的随机误差都服从正态分布;
(3)在生物学中,同一群体的某种特征都服从正态分布;
(4)在气象中,某地每年七月份的平均气温、平均湿度、降雨量等都服从正态分布。
正态分布的意义:
m 的意义
产品
尺寸
(mm)
总体平均数反映总体随机变量的
平均水平
x3
x4
x= μ
总体标准差反映总体随机变量的
集中与分散的程度
s的意义
给出下列三个正态密度曲线的函数表达式,请找出其均值μ和标准差σ。
(1)
(2)
( 3 )
0,1
1,2
-1,0.5
例题1:
1.下列函数是正态密度函数的是( ).
B
C
牛刀小试:
m
曲线函数:
两头低、中间高、左右对称
曲线性质:
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(4)曲线与x轴之间的面积为1
曲线性质:
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
曲线性质:
m-a
m+a
x=μ
知识小结:
内取值的概率。
区间
取值概率
68.26%
95.44%
99.74%
小概率事件
(μ-σ,μ+σ)
(μ-2σ,μ+2σ)
(μ-3σ,μ+3σ)
设一次数学考试中满分为150分,某班学生的分数服从正态分布N(110,202),如果这个班有54人,估计这个班的及格人数(不小于90分)和130分以上的人数
例题2
有一种精密零件,其尺寸X(单位mm)服从N(20,4)。若这批零件共有5000个,试求:
(1)尺寸在18mm~22mm间的零件的百分比;
(2)若尺寸在24mm~26mm间的零件为不合格,则不合格的零件大约有多少个?
例题3
