湖北省华中师大一附中2019-2020学年高二下学期网课课件——导数的运算(共40张PPT)
文档属性
| 名称 | 湖北省华中师大一附中2019-2020学年高二下学期网课课件——导数的运算(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 596.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-25 10:42:07 | ||
图片预览









文档简介
(共40张PPT)
导数的运算
单击输入您的封面副标题
1.y =f (x)的从x1到x2平均变化率为:
复习引入
3.用定义法求函数y=f(x)在点x0处的导数的方法步骤:
(1)求△y (2)求 (3)取极限
2. f(x)在点x0处的导数 (f(x)在点x0处的瞬时变化率)为: .
的几何意义为曲线在点 处的切线的斜率
4.
x
o
y
y=f(x)
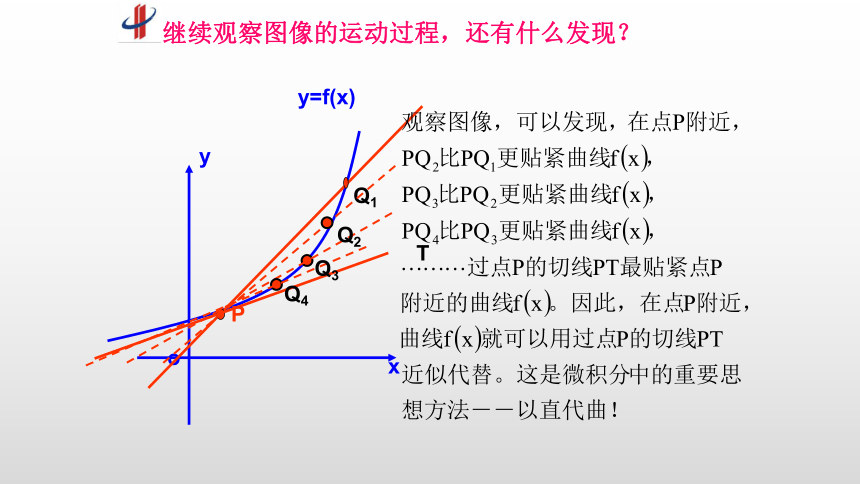
P
Q1
Q2
Q3
Q4
T
继续观察图像的运动过程,还有什么发现?
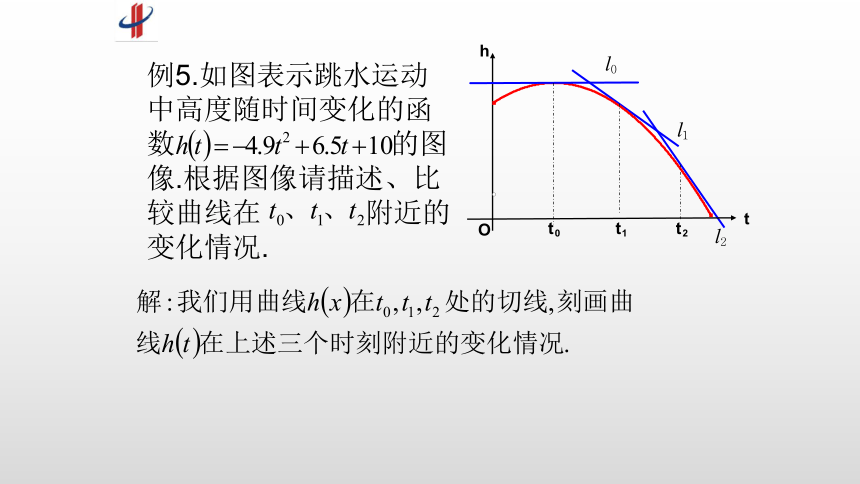
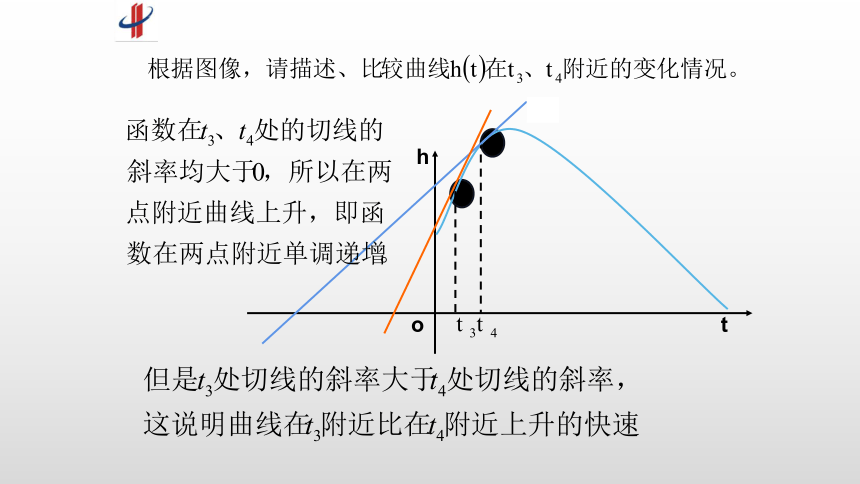
例5.如图表示跳水运动中高度随时间变化的函数 的图像.根据图像请描述、比较曲线在 附近的变化情况.
h
t
o
导函数
由函数 在 处求导数的过程可以看到,当 时, 是一个确定的数.那么,当 变化时, 便是 的一个函数,我们叫它为 的导函数 (简称导数). 即:
函数 在点 处的导数 与导数 的区别与联系:
(3)
(1)函数 在点 处的导数 是一个常数,与 有关.
这也是求函数在某点处的导数的方法之一
注意:
?
(2)函数的导数是一个函数,是指某一区间内
任意x,都有导数 与之对应.
导数的运算
用定义求下列函数的导数:
1. 2. 3.
4. 5. 6.
(1)函数f(x)=2的导数
(2) y=x的导数
(3) y=x2的导数
(6) 的导数
一.几个基本初等函数的导数
新课讲授
4x3
-5x-6
-2x-3
算一算
e
0
新课讲授
二.导数的运算法则
法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
(2)
法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
例1.求下列函数的导数
例题讲解
例2.求过点(2,0)且与曲线 相切的直线方程.
解:设所求切线与曲线的切点为 ,
所以切线方程为
点(2,0)在切线上,
所以所求直线方程为 x+y-2=0
1.复合函数的定义
对于两(多)个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,
三.复合函数的求导法则
新课讲授
练习:将复合函数分解成最简单函数
2.复合函数的求导法则
练习1.
解:
可看作是由
复合而成的. 因为
所以
例1.求下列函数的导数
例题讲解
练习2. 求函数
的导数.
解:
例2.求函数 的导数
例题讲解
例3.
(1)设
(2)已知函数 ,
(3)已知函数
-20
1
例3.
(1)若曲线 与曲线 在的它们的公共点处具有公共切线,则实数
.
(2)若存在过点(1,0)的直线与曲线 和 都相切,则a= .
(1)若曲线 与曲线 在的它们的公共点处具有公共切线,则实数 .
1
(2)若存在过点(1,0)的直线与曲线 和 都相切,则a= .
①
②当 时,切线方程为 ,(过程略),求得
(1)(2015新课标1)
在直角坐标系中,曲线: 与直线 交
两点,
①当 时,分别求曲线在点 处的切线方程;
② 轴上是否存在点 ,使得当 变动时,总有
?说明理由.
综合应用:
解:①不妨设 在右边, 在左边,由题设可得 ,
∵
故 在 处的导数为 , 在 处的切线
方程为 ,即 .
故 在 处的导数为 , 在 处的切线
方程为 ,即 .
-233
解:
等式两边取对数得
显函数:解析式中明显地用一个变量的代数式表示另一个变量时,称为显函数。显函数可以用y=f(x)来表示。
隐函数:如果方程F(x,y)=0能确定y是x的函数,那么称这种方式表示的函数是隐函数。
谢 谢 大 家
结 束
导数的运算
单击输入您的封面副标题
1.y =f (x)的从x1到x2平均变化率为:
复习引入
3.用定义法求函数y=f(x)在点x0处的导数的方法步骤:
(1)求△y (2)求 (3)取极限
2. f(x)在点x0处的导数 (f(x)在点x0处的瞬时变化率)为: .
的几何意义为曲线在点 处的切线的斜率
4.
x
o
y
y=f(x)
P
Q1
Q2
Q3
Q4
T
继续观察图像的运动过程,还有什么发现?
例5.如图表示跳水运动中高度随时间变化的函数 的图像.根据图像请描述、比较曲线在 附近的变化情况.
h
t
o
导函数
由函数 在 处求导数的过程可以看到,当 时, 是一个确定的数.那么,当 变化时, 便是 的一个函数,我们叫它为 的导函数 (简称导数). 即:
函数 在点 处的导数 与导数 的区别与联系:
(3)
(1)函数 在点 处的导数 是一个常数,与 有关.
这也是求函数在某点处的导数的方法之一
注意:
?
(2)函数的导数是一个函数,是指某一区间内
任意x,都有导数 与之对应.
导数的运算
用定义求下列函数的导数:
1. 2. 3.
4. 5. 6.
(1)函数f(x)=2的导数
(2) y=x的导数
(3) y=x2的导数
(6) 的导数
一.几个基本初等函数的导数
新课讲授
4x3
-5x-6
-2x-3
算一算
e
0
新课讲授
二.导数的运算法则
法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
(2)
法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
例1.求下列函数的导数
例题讲解
例2.求过点(2,0)且与曲线 相切的直线方程.
解:设所求切线与曲线的切点为 ,
所以切线方程为
点(2,0)在切线上,
所以所求直线方程为 x+y-2=0
1.复合函数的定义
对于两(多)个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,
三.复合函数的求导法则
新课讲授
练习:将复合函数分解成最简单函数
2.复合函数的求导法则
练习1.
解:
可看作是由
复合而成的. 因为
所以
例1.求下列函数的导数
例题讲解
练习2. 求函数
的导数.
解:
例2.求函数 的导数
例题讲解
例3.
(1)设
(2)已知函数 ,
(3)已知函数
-20
1
例3.
(1)若曲线 与曲线 在的它们的公共点处具有公共切线,则实数
.
(2)若存在过点(1,0)的直线与曲线 和 都相切,则a= .
(1)若曲线 与曲线 在的它们的公共点处具有公共切线,则实数 .
1
(2)若存在过点(1,0)的直线与曲线 和 都相切,则a= .
①
②当 时,切线方程为 ,(过程略),求得
(1)(2015新课标1)
在直角坐标系中,曲线: 与直线 交
两点,
①当 时,分别求曲线在点 处的切线方程;
② 轴上是否存在点 ,使得当 变动时,总有
?说明理由.
综合应用:
解:①不妨设 在右边, 在左边,由题设可得 ,
∵
故 在 处的导数为 , 在 处的切线
方程为 ,即 .
故 在 处的导数为 , 在 处的切线
方程为 ,即 .
-233
解:
等式两边取对数得
显函数:解析式中明显地用一个变量的代数式表示另一个变量时,称为显函数。显函数可以用y=f(x)来表示。
隐函数:如果方程F(x,y)=0能确定y是x的函数,那么称这种方式表示的函数是隐函数。
谢 谢 大 家
结 束
