北师大版七年级数学下册1.5平方差公式同步练习(2)(含答案)
文档属性
| 名称 | 北师大版七年级数学下册1.5平方差公式同步练习(2)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 64.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 15:02:29 | ||
图片预览

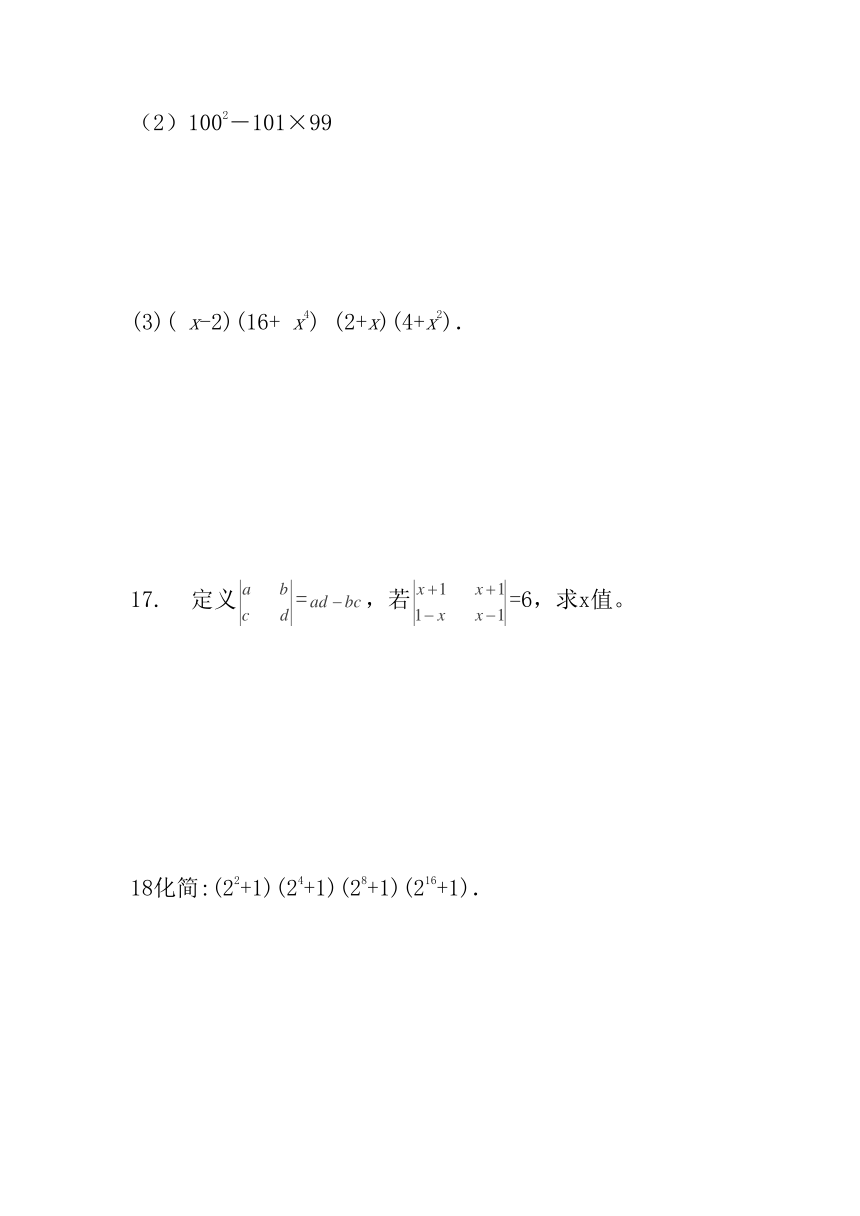
文档简介
北师大版七年级下学期1.5平方差公式
同步练习(2)
选择题
1.(x+6y)(x-6y)等于( )
A.x2-6y 2 B.x2-y 2 C.x2-36y 2 D.36x2-y 2
2.下列多项式能用平方差公式分解的因式有( )
(1)a2+b2 (2)x2-y2 (3)-m2+n2 (4)-a2b2 (5)-a6+4
A.2个 B.3个 C.4个 D.5个
3.下列因式分解正确的是( )
A .9a2+4b2=(9a+4b)(9a-4b) B.-s2-t2=(-s+t)(-s-t)
m2+(-n)2=(m+n)(m-n) D.-9+4y2=(3+2y)(2y-3)
下列各多项式中,能用平方差公式分解因式有是??? (??? )
? A.-x2+16??? ??B.x2+9??? ?
C.-x2-4??? ?D.x2-2y2
5.若a2-b2=6,a-b=3.则a+b的值为??? (??? )
? A.-2???B.-1??? ?C.1??? ?D.2
6.对于任整数n.多项式(4n+5)2-9都能( )
A.被6整除 B.被7整除 C.被8整除 D。被6或8整除
7.将多项式xn+3-xn+1分解因式,结果是( )
A.xn(x3-x) B.xn(x3-1)
C.xn+1(x2-1) D. Xn+1(x+1)(x-1)
8.如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )
A.a2+4 B.2a2+4a C.3a2﹣4a﹣4 D.4a2﹣a﹣2
9.请你计算:(1﹣x)(1+x),(1﹣x)(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+xn)的结果是( )
A.1﹣xn+1 B.1+xn+1 C.1﹣xn D.1+xn
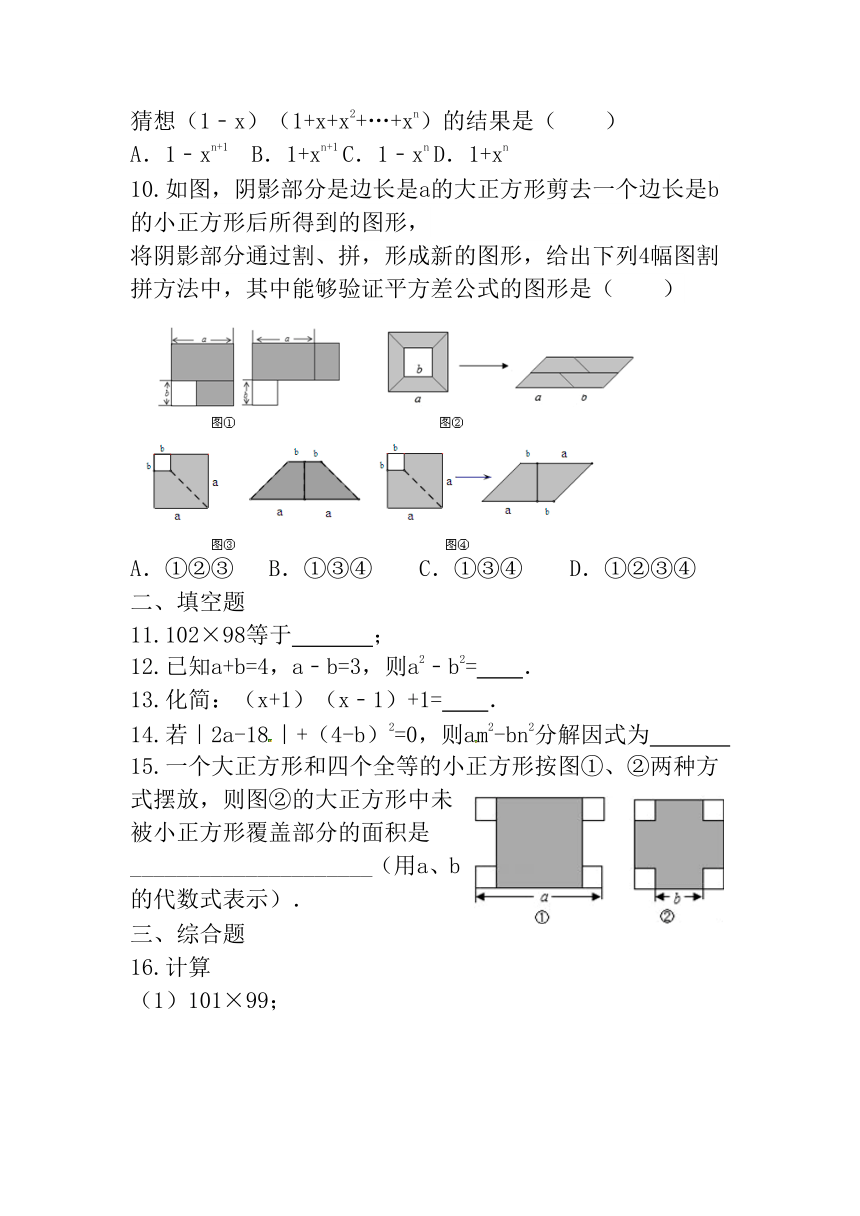
10.如图,阴影部分是边长是a的大正方形剪去一个边长是b的小正方形后所得到的图形,
将阴影部分通过割、拼,形成新的图形,给出下列4幅图割拼方法中,其中能够验证平方差公式的图形是( )
A.①②③ B.①③④ C.①③④ D.①②③④
填空题
11.102×98等于 ;
12.已知a+b=4,a﹣b=3,则a2﹣b2= .
13.化简:(x+1)(x﹣1)+1= .
14.若|2a-18|+(4-b)2=0,则am2-bn2分解因式为
15.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是_____________________(用a、b的代数式表示).
综合题
16.计算
(1)101×99;
(2)1002-101×99
(3)( x-2)(16+ x4) (2+x)(4+x2).
定义 =,若 =6,求x值。
18化简:(22+1)(24+1)(28+1)(216+1).
19.已知a=,b=,求:(a2-b2)2-(a2+b2)2的值。
20.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数.
(1)28和2012这两个数是神秘数吗?为什么?
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?
北师大版七年级下学期1.5平方差公式
同步练习(2)答案
选择题
1.C 2.B 3.D 4.A 5.D 6.D 7.D 8.C 9.A 10.D
二、填空题
11.9996
12.12
13.x2
14.(3m+2n)(3m-2n)
15.ab
三、综合题
16.(1)9999
(2)1
(3) x8-256.
17.
18.解:原式=(22-1)(22+1)(24+1)(28+1)(216+1)÷(22-1)
=(24-1)(24+1)(28+1)(216+1)÷(22-1)
=(28-1)(28+1)(216+1)÷(22-1)
=(28-1) (28+1) (216+1)÷(22-1)
=(216-1) (216+1)÷(22-1)=(232-1)÷(22-1)
=(232-1).
19.-2
20.解:(1)找规律:4=4×1=22-02,12=4×3=42-22,20=4×5=62-42,28=4×7=82-62,…,2012=4×503=5042-5022,所以28和2012都是神秘数.
(2)(2k+2) 2-(2 k) 2=4(2 k +1),因此由这两个连续偶数构造的神秘数是4的倍数.
(3)由(2)知,神秘数可以表示成4(2k+1),因为2 k +1是奇数,因此神秘数是4的倍数,但一定不是8的倍数.另一方面,设两个连续奇数为2 n +1和2 n -1,则(2 n +1) 2-(2n-1) 2=8n,即两个连续奇数的平方差是8的倍数.因此,两个连续奇数的平方差不是神秘数.
同步练习(2)
选择题
1.(x+6y)(x-6y)等于( )
A.x2-6y 2 B.x2-y 2 C.x2-36y 2 D.36x2-y 2
2.下列多项式能用平方差公式分解的因式有( )
(1)a2+b2 (2)x2-y2 (3)-m2+n2 (4)-a2b2 (5)-a6+4
A.2个 B.3个 C.4个 D.5个
3.下列因式分解正确的是( )
A .9a2+4b2=(9a+4b)(9a-4b) B.-s2-t2=(-s+t)(-s-t)
m2+(-n)2=(m+n)(m-n) D.-9+4y2=(3+2y)(2y-3)
下列各多项式中,能用平方差公式分解因式有是??? (??? )
? A.-x2+16??? ??B.x2+9??? ?
C.-x2-4??? ?D.x2-2y2
5.若a2-b2=6,a-b=3.则a+b的值为??? (??? )
? A.-2???B.-1??? ?C.1??? ?D.2
6.对于任整数n.多项式(4n+5)2-9都能( )
A.被6整除 B.被7整除 C.被8整除 D。被6或8整除
7.将多项式xn+3-xn+1分解因式,结果是( )
A.xn(x3-x) B.xn(x3-1)
C.xn+1(x2-1) D. Xn+1(x+1)(x-1)
8.如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )
A.a2+4 B.2a2+4a C.3a2﹣4a﹣4 D.4a2﹣a﹣2
9.请你计算:(1﹣x)(1+x),(1﹣x)(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+xn)的结果是( )
A.1﹣xn+1 B.1+xn+1 C.1﹣xn D.1+xn
10.如图,阴影部分是边长是a的大正方形剪去一个边长是b的小正方形后所得到的图形,
将阴影部分通过割、拼,形成新的图形,给出下列4幅图割拼方法中,其中能够验证平方差公式的图形是( )
A.①②③ B.①③④ C.①③④ D.①②③④
填空题
11.102×98等于 ;
12.已知a+b=4,a﹣b=3,则a2﹣b2= .
13.化简:(x+1)(x﹣1)+1= .
14.若|2a-18|+(4-b)2=0,则am2-bn2分解因式为
15.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是_____________________(用a、b的代数式表示).
综合题
16.计算
(1)101×99;
(2)1002-101×99
(3)( x-2)(16+ x4) (2+x)(4+x2).
定义 =,若 =6,求x值。
18化简:(22+1)(24+1)(28+1)(216+1).
19.已知a=,b=,求:(a2-b2)2-(a2+b2)2的值。
20.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数.
(1)28和2012这两个数是神秘数吗?为什么?
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?
北师大版七年级下学期1.5平方差公式
同步练习(2)答案
选择题
1.C 2.B 3.D 4.A 5.D 6.D 7.D 8.C 9.A 10.D
二、填空题
11.9996
12.12
13.x2
14.(3m+2n)(3m-2n)
15.ab
三、综合题
16.(1)9999
(2)1
(3) x8-256.
17.
18.解:原式=(22-1)(22+1)(24+1)(28+1)(216+1)÷(22-1)
=(24-1)(24+1)(28+1)(216+1)÷(22-1)
=(28-1)(28+1)(216+1)÷(22-1)
=(28-1) (28+1) (216+1)÷(22-1)
=(216-1) (216+1)÷(22-1)=(232-1)÷(22-1)
=(232-1).
19.-2
20.解:(1)找规律:4=4×1=22-02,12=4×3=42-22,20=4×5=62-42,28=4×7=82-62,…,2012=4×503=5042-5022,所以28和2012都是神秘数.
(2)(2k+2) 2-(2 k) 2=4(2 k +1),因此由这两个连续偶数构造的神秘数是4的倍数.
(3)由(2)知,神秘数可以表示成4(2k+1),因为2 k +1是奇数,因此神秘数是4的倍数,但一定不是8的倍数.另一方面,设两个连续奇数为2 n +1和2 n -1,则(2 n +1) 2-(2n-1) 2=8n,即两个连续奇数的平方差是8的倍数.因此,两个连续奇数的平方差不是神秘数.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
