华东师大版八年级下册第17章函数及其图象单元测试卷 附答案
文档属性
| 名称 | 华东师大版八年级下册第17章函数及其图象单元测试卷 附答案 |  | |
| 格式 | zip | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 14:58:46 | ||
图片预览




文档简介
华东师大版八年级下册第17章《函数及其图象》单元测试卷
满分100分
班级:________姓名:________学号:________成绩:________
一.选择题(共10小题,满分30分)
1.若正比例函数y=kx的图象经过点(3,﹣9),则k的值为( )
A.﹣3 B.3 C.﹣ D.
2.在球的体积公式V=πR3中,下列说法正确的是( )
A.V、π、R是变量,为常量 B.V、R是变量,π为常量
C.V、R是变量,、π为常量 D.V、R是变量,为常量
3.下列函数中,属于反比例函数的是( )
A.y=﹣2x B.y=kx﹣1 C.y= D.y=
4.若反比例函数y=的图象经过点(2,﹣1),则该反比例函数的图象在( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
5.若点A(a+1,b﹣2)在第二象限,则点B(﹣a,b+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在一次函数y=ax﹣a中,y随x的增大而减小,则其图象可能是( )
A. B.
C. D.
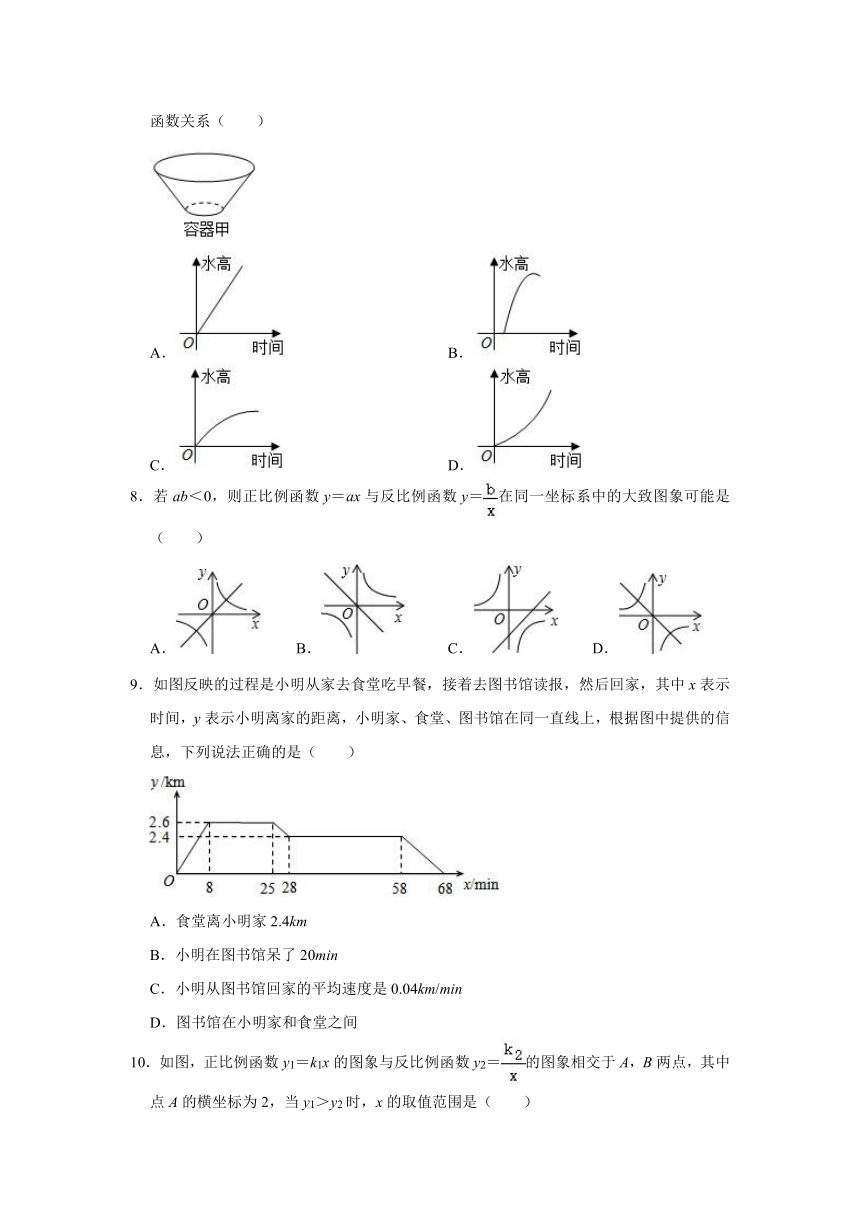
7.如图,向容器甲中匀速的注水,下面哪一个图象可以大致刻画容器中水的高度与时间的函数关系( )
A. B.
C. D.
8.若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是( )
A. B. C. D.
9.如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间
10.如图,正比例函数y1=k1x的图象与反比例函数y2=的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
A.x<﹣2或x>2 B.x<﹣2或0<x<2
C.﹣2<x<0或0<x<2 D.﹣2<x<0或x>2
二.填空题(共6小题,满分18分)
11.若函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,则a= .
12.点M在第四象限,它到x轴的距离是4,到y轴的距离是5,则点M的坐标为 .
13.如图,若一次函数y=﹣2x+b的图象与两坐标轴分别交于A,B两点,点A的坐标为(0,3),则不等式﹣2x+b>0的解集为 .
14.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为 .
15.如图,一次函数y=mx与反比例函数y=的图象交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=3,则k的值是 .
16.在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(),那么点An的纵坐标是 .
三.解答题(共6小题。满分52分)
17.一次函数图象经过(3,1),(2,0)两点.
(1)求这个一次函数的解析式;
(2)求当x=6时,y的值.
18.反比例函数y=与一次函数y=2x﹣4的图象都过A(m,2).
(1)求A点坐标;
(2)求反比例函数解析式.
19.某酒厂生产A、B两种品牌的酒,每天两种酒共生产600瓶,每种酒每瓶的成本和利润如下表所示.设每天共获利y元,每天生产A种品牌的酒x瓶.
A B
成本(元) 50 35
利润(元) 20 15
(1)请写出y关于x的函数关系式;
(2)如果该厂每天至少投入成本25000元,且生产B种品牌的酒不少于全天产量的55%,那么共有几种生产方案?并求出每天至少获利多少元?
20.已知函数y=(2m﹣2)x+m+1,
(1)m为何值时,图象过原点.
(2)已知y随x增大而增大,求m的取值范围.
(3)函数图象与y轴交点在x轴上方,求m取值范围.
(4)图象过一、二、四象限,求m的取值范围.
21.小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是 米,小红在商店停留了 分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分?
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?
22.已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
参考答案
一.选择题(共10小题)
1.【解答】解:∵正比例函数y=kx的图象经过点(3,﹣9),
∴﹣9=3k,
∴k=﹣3.
故选:A.
2.【解答】解:在球的体积公式V=πR3中,V,R是变量,,π是常量,
故选:C.
3.【解答】解:A.y=﹣2x是正比例函数,不符合题意;
B.y=kx﹣1只有当k≠0时才符合反比例函数定义,不符合题意;
C.y=﹣是反比例函数,符合题意;
D.y=不是反比例函数,不符合题意;
故选:C.
4.【解答】解:点(2,﹣1)在第四象限,则该反比例函数的图象的两个分支在第二、四象限.
故选:D.
5.【解答】解:由A(a+1,b﹣2)在第二象限,得
a+1<0,b﹣2>0.
解得a<﹣1,b>2.
由不等式的性质,得
﹣a>1,b+1>3,
点B(﹣a,b+1)在第一象限,
故选:A.
6.【解答】解:由y=ax﹣a中,y随x的增大而减小,得a<0,﹣a>0,
故B正确.
故选:B.
7.【解答】解:由容器的形状可知:
注入水的高度随着时间的增长越来越高,
但增长的速度越来越慢,
即图象开始陡峭,后来趋于平缓,
故选:C.
8.【解答】解:∵ab<0,∴分两种情况:
(1)当a>0,b<0时,正比例函数y=ax数的图象过原点、第一、三象限,反比例函数图象在第二、四象限,无此选项;
(2)当a<0,b>0时,正比例函数的图象过原点、第二、四象限,反比例函数图象在第一、三象限,选项B符合.
故选:B.
9.【解答】解:A.从图中看出,食堂离小明家2.6km.选项错误;
B.小明在图书馆待了58﹣28=30min.选项错误;
C.图书馆离小明家2.4km,小明从图书馆回家所用时间是68﹣58=10min,所以小明从图书馆回家的平均速度是2.4÷10=0.24km/min.故选项错误;
D.从图象可以看出,食堂离小明家2.6km,图书馆离小明家2.4km,所以,图书馆在小明家和食堂之间.故选项正确.
故选:D.
10.【解答】解:∵反比例函数与正比例函数的图象均关于原点对称,
∴A、B两点关于原点对称,
∵点A的横坐标为2,
∴点B的横坐标为﹣2,
∵由函数图象可知,当﹣2<x<0或x>2时函数y1=k1x的图象在y2=的上方,
∴当y1>y2时,x的取值范围是﹣2<x<0或x>2.
故选:D.
二.填空题(共6小题)
11.【解答】解:∵函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,
∴a=±3,
又∵a≠3,
∴a=﹣3.
故答案为:﹣3.
12.【解答】解:因为点M在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点M到x轴的距离为4,到y轴的距离为5,
所以点M的坐标为(5,﹣4).
故答案为:(5,﹣4).
13.【解答】解:∵一次函数y=﹣2x+b的图象与y轴交于点A(0,3),
∴b=3,
∴一次函数解析式为y=﹣2x+3,
解不等式﹣2x+3>0得x<.
故答案为x<.
14.【解答】解:根据三个函数图象所在象限可得a<0,b>0,c>0,
再根据直线越陡,|k|越大,则b>c.
则b>c>a,
故答案为:a<c<b.
15.【解答】解:由题意得:S△ABM=2S△AOM=3,S△AOM=|k|=,则k=3.
故答案为:3.
16.【解答】解:∵A1(1,1),A2(,)在直线y=kx+b上,
∴,
解得,
∴直线解析式为y=x+,
如图,设直线与x轴、y轴的交点坐标分别为N、M,
当x=0时,y=,
当y=0时,x+=0,解得x=﹣4,
∴点M、N的坐标分别为M(0,),N(﹣4,0),
作A1C1⊥x轴于点C1,A2C2⊥x轴于点C2,A3C3⊥x轴于点C3,
∵A1(1,1),A2(,),
∴OB2=OB1+B1B2=2×1+2×=2+3=5,
∵△B2A3B3是等腰直角三角形,
∴A3C3=B2C3,
∴A3C3==()2,
同理可求,第四个等腰直角三角形A4C4==()3,
依此类推,点An的纵坐标是()n﹣1.
故答案为:()n﹣1.
三.解答题(共6小题)
17.【解答】解:(1)设一次函数解析式为y=kx+b,
把(3,1),(2,0)代入得,解得,
所以一次函数解析式为y=x﹣2;
(2)当x=6时,y=x﹣2=6﹣2=4.
18.【解答】解:(1)将点A(m,2)代入y=2x﹣4得:
2m﹣4=2,
解得:m=3,
∴点A的坐标为(3,2);
(2)将点A(3,2)代入y=得:k=6,
∴反比例函数解析式为y=.
19.【解答】解:(1)由题意,每天生产A种品牌的酒x瓶,则每天生产B种品牌的酒(600﹣x)瓶,
∴y=20x+15(600﹣x)=9000+5x.
(2)根据题意得:,
解得:266≤x≤270,
∵x为整数,
∴x=267、268、269、270,
该酒厂共有4种生产方案:
①生产A种品牌的酒267瓶,B种品牌的酒333瓶;
②生产A种品牌的酒268瓶,B种品牌的酒332瓶;
③生产A种品牌的酒269瓶,B种品牌的酒331瓶;
④生产A种品牌的酒270瓶,B种品牌的酒330瓶;
∵每天获利y=9000+5x,y是关于x的一次函数,且随x的增大而增大,
∴当x=267时,y有最小值,y最小=9000+5×267=10335元.
20.【解答】解:(1)∵函数图象过原点,
∴m+1=0,即m=﹣1;
(2)∵y随x增大而增大,
∴2m﹣2>0,解得m>1;
(3)∵函数图象与y轴交点在x轴上方,
∴,解得即m>﹣1且m≠1;
(4)∵图象过一、二、四象限,
∴,解得﹣1<m<1.
21.【解答】解:(1)根据图象舅舅家纵坐标为1500,小红家的纵坐标为0,
故小红家到舅舅家的路程是1500米;据题意,小红在商店停留的时间为从8分到12分,故小红在商店停留了4分钟.
故答案为:1500,4;
(2)根据图象,12≤x≤14时,直线最陡,
故小红在12﹣14分钟最快,速度为=450米/分.
(3)读图可得:小红共行驶了1200+600+900=2700米,共用了14分钟.
22.【解答】解:(1)把A(﹣4,2)代入y=,得m=2×(﹣4)=﹣8,
所以反比例函数解析式为y=﹣,
把B(n,﹣4)代入y=﹣,得﹣4n=﹣8,
解得n=2,
把A(﹣4,2)和B(2,﹣4)代入y=kx+b,得
,
解得,
所以一次函数的解析式为y=﹣x﹣2;
(2)y=﹣x﹣2中,令y=0,则x=﹣2,
即直线y=﹣x﹣2与x轴交于点C(﹣2,0),
∴S△AOB=S△AOC+S△BOC=×2×2+×2×4=6;
(3)由图可得,不等式kx+b﹣>0的解集为:x<﹣4或0<x<2.
