2020北师版九上数学6.2反比例函数的图象与性质第1课时习题课件(17张PPT)
文档属性
| 名称 | 2020北师版九上数学6.2反比例函数的图象与性质第1课时习题课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 18:57:45 | ||
图片预览






文档简介
课件17张PPT。2 反比例函数的图象与性质
第1课时1.反比例函数的图象
反比例函数的图象形状是_______,它们都不会与_______相交.
2.反比例函数图象的位置
(1)当k>0时,两支曲线分别位于第 _______象限.
(2)当k<0时,两支曲线分别位于第 _______象限.双曲线坐标轴一、三二、四3.反比例函数图象的对称性
(1)轴对称:对称轴为_______________所在的直线.
(2)中心对称:对称中心是_________.各象限角平分线坐标原点【思维诊断】(打“√”或“×”)
1.反比例函数 的图象在第二、四象限. ( )
2.画反比例函数图象时x不能取0. ( )
3.反比例函数图象与x轴,y轴都没有交点. ( )
4.反比例函数 过点(-1,3),则它的图象在第一、三象
限. ( )×√√×知识点一 反比例函数的图象
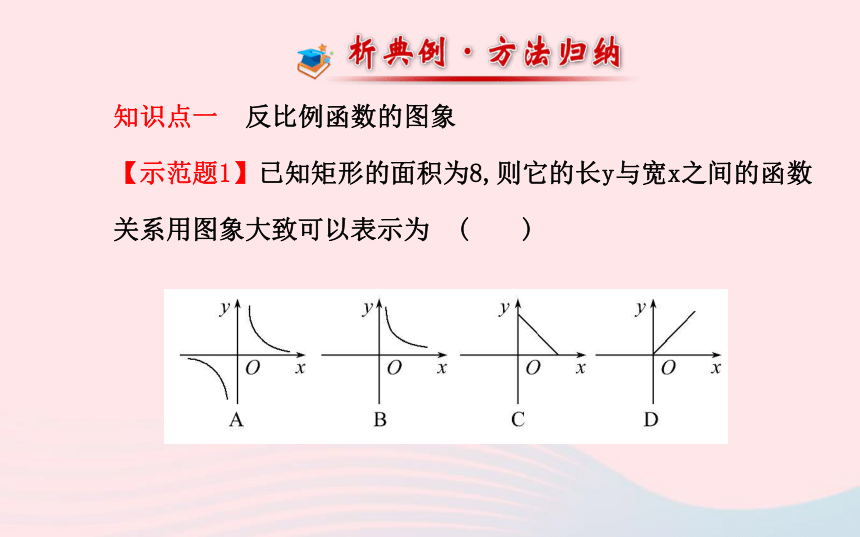
【示范题1】已知矩形的面积为8,则它的长y与宽x之间的函数关系用图象大致可以表示为 ( )【思路点拨】由矩形的面积列出函数表达式,再根据实际问题
得出正确选项.
【自主解答】选B.由矩形的面积是8可知,xy=8,y= ,又x>0,
y>0,所以图象是在第一象限的一支.【想一想】
反比例函数 的图象在第一、三象限,你能确定m的取
值范围吗?
提示:m>1.
先由图象在第一、三象限判断m-1的符号,再解关于m的不等式.【微点拨】
1.判断函数的图象先判断函数的类型,再考虑函数自变量的取值范围.
2.反比例函数的图象是双曲线,两个分支分别位于两个象限,但在解决实际问题时还要注意实际问题中自变量的取值范围,有时实际问题中的反比例函数图象可能只是它的一个分支.【方法一点通】
反比例函数图象位置与系数k的符号的关系
1.k>0 图象在第一、三象限.
2.k<0 图象在第二、四象限.
注:不论k是正的还是负的,函数图象与坐标轴都不会相交.知识点二 反比例函数图象与一次函数图象的结合
【示范题2】若ab<0,则正比例函数y=ax和反
比例函数 在同一坐标系中的大致图象可能是 ( )【教你解题】【想一想】
反比例函数y= 与正比例函数y=3x有交点吗?
提示:有交点,因为反比例函数的系数k1=2与正比例函数的系数k2=3是同号,所以它们都过第一、三象限,一定有两个交点.【备选例题】(1)若反比例函数y= 的图象
过点(-2,1),则一次函数y=kx-k的图象过 ( )
A.第一、二、四象限
B.第一、三、四象限
C.第二、三、四象限
D.第一、二、三象限【解析】选A.把点的坐标(-2,1)代入反比例函数的表达式y= ,
得k=-2,因此一次函数y=kx-k的表达式为y=-2x+2,图象与y轴交
点为(0,2),与x轴交点为(1,0),画图可知,图象经过第一、二、
四象限.(2)在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数y= 的图象没有公共点,则( )
A.k1+k2<0 B.k1+k2>0 C.k1k2<0 D.k1k2>0【解析】选C.∵在同一直角坐标系中,若正比例函数y=k1x的图
象与反比例函数y= 的图象没有公共点,∴正比例函数y=k1x
的图象与反比例函数y= 的图象不可能同时出现在同一个象
限,∴若k1<0,则k2>0;若k1>0,则k2<0.即k1与k2异号,即k1k2<0.【方法一点通】
正比例函数与反比例函数图象的位置判断
1.正比例函数y=kx的图象所在的象限由k的值确定:
(1)k>0时,图象过一、三象限.
(2)k<0时,图象过第二、四象限.
2.反比例函数y= 的图象所在的象限由k的值确定:
(1)k>0时,图象在第一、三象限.
(2)k<0时,图象在第二、四象限.
第1课时1.反比例函数的图象
反比例函数的图象形状是_______,它们都不会与_______相交.
2.反比例函数图象的位置
(1)当k>0时,两支曲线分别位于第 _______象限.
(2)当k<0时,两支曲线分别位于第 _______象限.双曲线坐标轴一、三二、四3.反比例函数图象的对称性
(1)轴对称:对称轴为_______________所在的直线.
(2)中心对称:对称中心是_________.各象限角平分线坐标原点【思维诊断】(打“√”或“×”)
1.反比例函数 的图象在第二、四象限. ( )
2.画反比例函数图象时x不能取0. ( )
3.反比例函数图象与x轴,y轴都没有交点. ( )
4.反比例函数 过点(-1,3),则它的图象在第一、三象
限. ( )×√√×知识点一 反比例函数的图象
【示范题1】已知矩形的面积为8,则它的长y与宽x之间的函数关系用图象大致可以表示为 ( )【思路点拨】由矩形的面积列出函数表达式,再根据实际问题
得出正确选项.
【自主解答】选B.由矩形的面积是8可知,xy=8,y= ,又x>0,
y>0,所以图象是在第一象限的一支.【想一想】
反比例函数 的图象在第一、三象限,你能确定m的取
值范围吗?
提示:m>1.
先由图象在第一、三象限判断m-1的符号,再解关于m的不等式.【微点拨】
1.判断函数的图象先判断函数的类型,再考虑函数自变量的取值范围.
2.反比例函数的图象是双曲线,两个分支分别位于两个象限,但在解决实际问题时还要注意实际问题中自变量的取值范围,有时实际问题中的反比例函数图象可能只是它的一个分支.【方法一点通】
反比例函数图象位置与系数k的符号的关系
1.k>0 图象在第一、三象限.
2.k<0 图象在第二、四象限.
注:不论k是正的还是负的,函数图象与坐标轴都不会相交.知识点二 反比例函数图象与一次函数图象的结合
【示范题2】若ab<0,则正比例函数y=ax和反
比例函数 在同一坐标系中的大致图象可能是 ( )【教你解题】【想一想】
反比例函数y= 与正比例函数y=3x有交点吗?
提示:有交点,因为反比例函数的系数k1=2与正比例函数的系数k2=3是同号,所以它们都过第一、三象限,一定有两个交点.【备选例题】(1)若反比例函数y= 的图象
过点(-2,1),则一次函数y=kx-k的图象过 ( )
A.第一、二、四象限
B.第一、三、四象限
C.第二、三、四象限
D.第一、二、三象限【解析】选A.把点的坐标(-2,1)代入反比例函数的表达式y= ,
得k=-2,因此一次函数y=kx-k的表达式为y=-2x+2,图象与y轴交
点为(0,2),与x轴交点为(1,0),画图可知,图象经过第一、二、
四象限.(2)在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数y= 的图象没有公共点,则( )
A.k1+k2<0 B.k1+k2>0 C.k1k2<0 D.k1k2>0【解析】选C.∵在同一直角坐标系中,若正比例函数y=k1x的图
象与反比例函数y= 的图象没有公共点,∴正比例函数y=k1x
的图象与反比例函数y= 的图象不可能同时出现在同一个象
限,∴若k1<0,则k2>0;若k1>0,则k2<0.即k1与k2异号,即k1k2<0.【方法一点通】
正比例函数与反比例函数图象的位置判断
1.正比例函数y=kx的图象所在的象限由k的值确定:
(1)k>0时,图象过一、三象限.
(2)k<0时,图象过第二、四象限.
2.反比例函数y= 的图象所在的象限由k的值确定:
(1)k>0时,图象在第一、三象限.
(2)k<0时,图象在第二、四象限.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
