2020北师版九上数学第六章反比例函数阶段复习习题课件(33张PPT)
文档属性
| 名称 | 2020北师版九上数学第六章反比例函数阶段复习习题课件(33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 19:04:10 | ||
图片预览

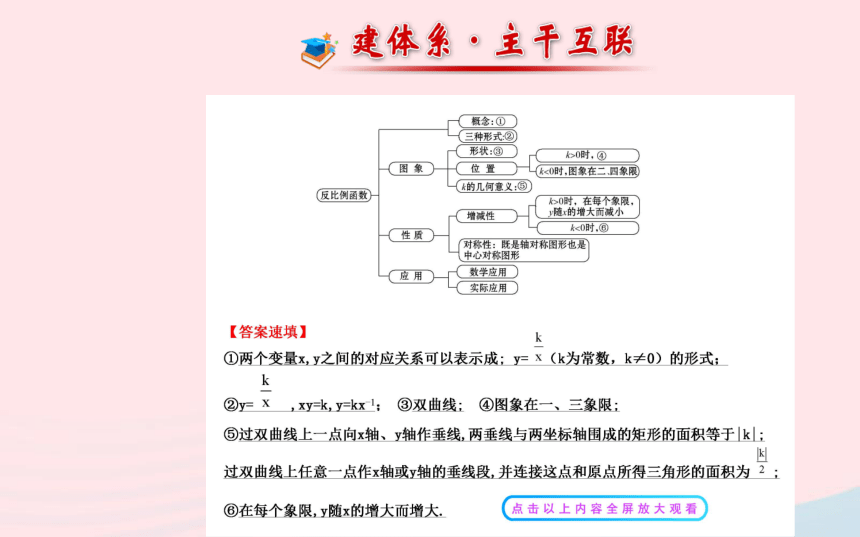








文档简介
课件33张PPT。阶段复习课
第 六 章主题1 反比例函数的概念、图象和性质
【主题训练1】已知两点P1(x1,y1),P2(x2,y2)
在反比例函数y= 的图象上,当x1>x2>0时,下列结论正确的是
( )
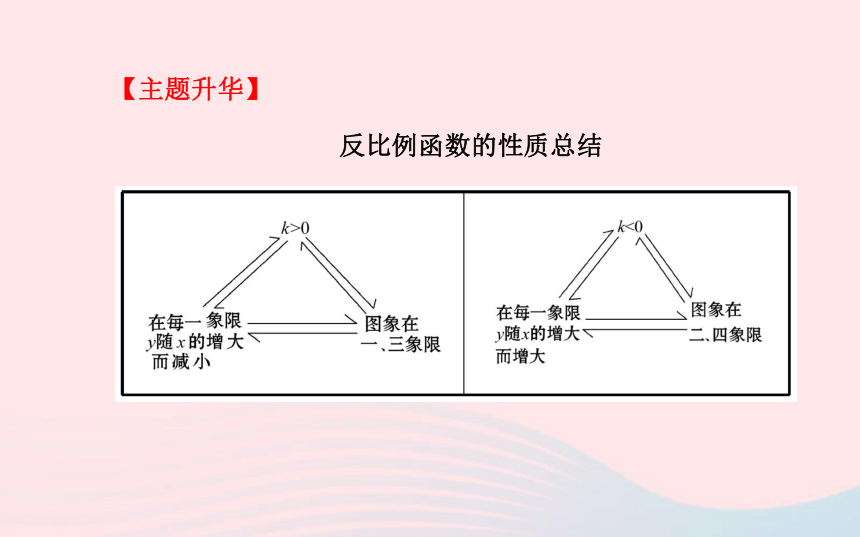
A.0C.y10,∴反比例函数图象在第一、三象限,且在每个象限内,y随x的增大而减小,又∵x1>x2>0,∴0反比例函数的性质总结【备选例题】下列函数中,图象经过点(1,-1)的反比例函数关系式是 ( )
【解析】选A.由反比例函数的概念与图象可知把点(1,-1)代入A,B,C,D四个选项的关系式只有A选项正确.1.已知反比例函数y= 的图象经过点(2, -2),则k的值为 ( )
A.4 B.- C.-4 D.-2
【解析】选C.∵反比例函数y= 的图象经过点(2,-2),
∴-2= ,解得k=-4.【变式训练】已知双曲线y= 经过点
(-1,2),那么k的值等于 .
【解析】将点(-1,2)代入
解得k=-3.
答案:-32.下列四个点中,在反比例函数y= 的图
象上的是 ( )
A.(3,-2) B.(3,2) C.(2,3) D.(-2,-3)
【解析】选A.由函数关系式知,xy=-6,所给选项中,只有A满足.【方法技巧】判断点是否在函数图象上的方法
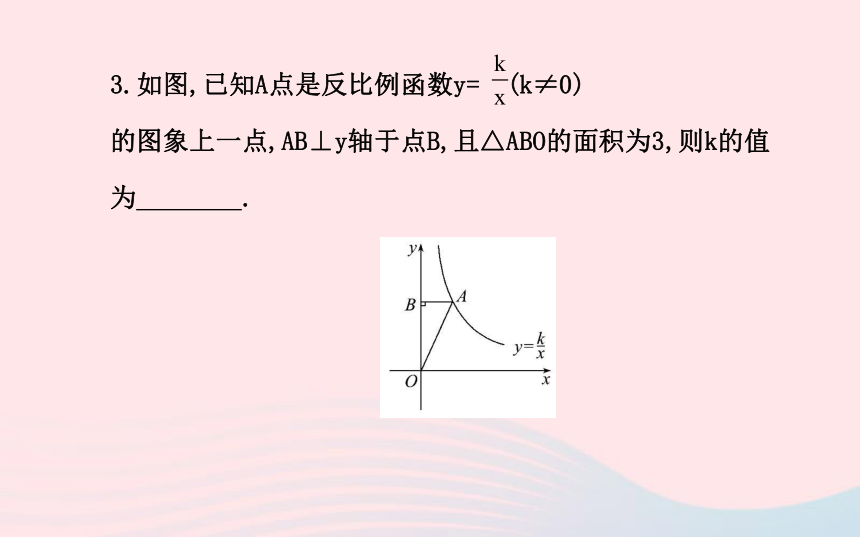
判断一个点在不在函数图象上,直接将所给的点代入函数关系式,若满足函数关系式,则在函数图象上,若不满足,则不在函数图象上.3.如图,已知A点是反比例函数y= (k≠0)
的图象上一点,AB⊥y轴于点B,且△ABO的面积为3,则k的值
为 .【解析】由于A是图象上任意一点,则S△ABO= |k|=3,
又∵反比例函数的图象在一象限,k>0,∴k=6.
答案:64.点(2,y1),(3,y2)在函数y=- 的图象上,
则y1 y2(填“>”或“=”或“<”).
【解析】因为比例系数k=-2<0,而2<3,所以由“当k<0时,函数
图象位于第二,四象限,在每一个象限内,y随x的增大而增大”
可知y1答案:<【一题多解】当x=2时,y1=- =-1;当x=3时,
y2=- ;所以y1答案:<主题2 用待定系数法求反比例函数表达式
【主题训练2】如图,在平面直角坐标系中,双曲线y= 和直线y=kx+b交于A,B两点,点A的坐标为(-3,2), BC⊥y轴于点C,且OC=6BC.
(1)求双曲线和直线的关系式.
(2)直接写出不等式 >kx+b的解集.【自主解答】(1)∵点A(-3,2)在双曲线y= 上,
∴2= ∴m=-6,
∴双曲线的关系式为y=- .
∵点B在双曲线y=- 上,且OC=6BC,设点B的坐标为(a,-6a)
(a>0),∴-6a=- ,解得:a=1(负值舍去).
∴点B的坐标为(1,-6).
∵直线y=kx+b过点A,B,
∴直线的关系式为y=-2x-4.(2)在y轴的左侧,当 >kx+b时,双曲线的图象在直线的上方,
所以x的取值范围是:-3kx+b时,双曲
线的图象在直线的上方,所以x的取值范围是x>1,所以不等式
>kx+b的解集为:-31.【主题升华】
待定系数法确定反比例函数表达式的步骤
(1)设:设出函数的表达式y= (k≠0).
(2)代:将一组对应的x,y的值代入反比例函数的表达式,确定k的值.
(3)写:写出反比例函数的表达式.如图,在平面直角坐
标系中,直线 与x轴交于点A,与双
曲线y= 在第一象限内交于点B,BC⊥x轴于
点C,OC=2AO,求双曲线的表达式.【解析】∵直线
∴A(-1,0),∴OA =1.
∵OC=2OA,∴OC =2.
令x=2,得:
又∵B在双曲线上,
∴k =3.∴双曲线的表达式为 主题3 反比例函数的应用
【主题训练3】某地资源总量Q一定,该地人均资源享有量 与人口数n的函数关系图象是 ( )【自主解答】选B.根据资源总量Q=人均资源享有量 ×人口数
n得, 其中Q是常量且Q>0得 与n成反比例函数关系,图
象为其在第一象限的部分.【主题升华】
用反比例函数解决实际问题“四步法”
(1)分析题意:找出问题中的常量、变量(有时常量、变量以图象的形式给出),并且理清常量与变量之间的关系.
(2)设关系式:根据常量与变量之间的关系,设出反比例函数关系式.
(3)求解系数:利用待定系数法确定反比例函数关系式.
(4)确定答案:根据反比例函数的图象与性质解决实际问题.【备选例题】已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式.
(2)观察图象,当x>0时,直接写出y1>y2时自变量x的取值范围.
(3)如果点C与点A关于x轴对称,求△ABC的面积.【自主解答】(1)∵函数y1= 的图象过点A(1,4),
即4= ,∴k=4,即y1= .
又∵点B(m,-2)在y1= 上,
∴m=-2,∴B(-2,-2).
又∵一次函数y2=ax+b过A,B两点,
即
∴y2=2x+2.
综上可得y1= ,y2=2x+2.(2)当x>0时,要使y1>y2,即函数y1的图象总在函数y2的图象上方,
∴0(3)∵点C与点A关于x轴对称,
∴C(1,-4).
过点B作BD⊥AC,垂足为D,如图,则D(1,-2),
于是△ABC的高BD=1-(-2)=3,
底为AC=4-(-4)=8.
∴S△ABC= AC·BD= ×8×3=12.1.已知矩形的面积为36cm2,相邻两条边长分别为xcm和ycm,则y与x之间的函数图象大致是 ( )【解析】选A.依题意,xy=36,∴y= ,其图象为位于一、三象
限的双曲线.又∵矩形边长x>0,所以图象为第一象限的一个分
支,且y随x的增大而减小.2.为了更好保护水资源,造福人类.某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V = Sh(V≠0),则S关于h的函数图象大致是 ( )【解析】选C.∵V = Sh(V≠0,其中V为常量),∴S= (h>0),则
S关于h的函数图象是双曲线在第一象限内的一部分,只有C符合.3.如图,等边三角形ABC放置在平面直角坐标系中,已知A(0,0),B(6,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的关系式.
(2)将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.【解析】(1)过点C作CH⊥x轴,垂足为H.∵△ABC是等边三角形,∴AH= AB=3,∴
设反比例函数的关系式为
即 (2)∵将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,∴设此时的点B坐标为(6,n),∴6n=9 ,解得n=
第 六 章主题1 反比例函数的概念、图象和性质
【主题训练1】已知两点P1(x1,y1),P2(x2,y2)
在反比例函数y= 的图象上,当x1>x2>0时,下列结论正确的是
( )
A.0
【解析】选A.由反比例函数的概念与图象可知把点(1,-1)代入A,B,C,D四个选项的关系式只有A选项正确.1.已知反比例函数y= 的图象经过点(2, -2),则k的值为 ( )
A.4 B.- C.-4 D.-2
【解析】选C.∵反比例函数y= 的图象经过点(2,-2),
∴-2= ,解得k=-4.【变式训练】已知双曲线y= 经过点
(-1,2),那么k的值等于 .
【解析】将点(-1,2)代入
解得k=-3.
答案:-32.下列四个点中,在反比例函数y= 的图
象上的是 ( )
A.(3,-2) B.(3,2) C.(2,3) D.(-2,-3)
【解析】选A.由函数关系式知,xy=-6,所给选项中,只有A满足.【方法技巧】判断点是否在函数图象上的方法
判断一个点在不在函数图象上,直接将所给的点代入函数关系式,若满足函数关系式,则在函数图象上,若不满足,则不在函数图象上.3.如图,已知A点是反比例函数y= (k≠0)
的图象上一点,AB⊥y轴于点B,且△ABO的面积为3,则k的值
为 .【解析】由于A是图象上任意一点,则S△ABO= |k|=3,
又∵反比例函数的图象在一象限,k>0,∴k=6.
答案:64.点(2,y1),(3,y2)在函数y=- 的图象上,
则y1 y2(填“>”或“=”或“<”).
【解析】因为比例系数k=-2<0,而2<3,所以由“当k<0时,函数
图象位于第二,四象限,在每一个象限内,y随x的增大而增大”
可知y1
y2=- ;所以y1
【主题训练2】如图,在平面直角坐标系中,双曲线y= 和直线y=kx+b交于A,B两点,点A的坐标为(-3,2), BC⊥y轴于点C,且OC=6BC.
(1)求双曲线和直线的关系式.
(2)直接写出不等式 >kx+b的解集.【自主解答】(1)∵点A(-3,2)在双曲线y= 上,
∴2= ∴m=-6,
∴双曲线的关系式为y=- .
∵点B在双曲线y=- 上,且OC=6BC,设点B的坐标为(a,-6a)
(a>0),∴-6a=- ,解得:a=1(负值舍去).
∴点B的坐标为(1,-6).
∵直线y=kx+b过点A,B,
∴直线的关系式为y=-2x-4.(2)在y轴的左侧,当 >kx+b时,双曲线的图象在直线的上方,
所以x的取值范围是:-3
线的图象在直线的上方,所以x的取值范围是x>1,所以不等式
>kx+b的解集为:-3
待定系数法确定反比例函数表达式的步骤
(1)设:设出函数的表达式y= (k≠0).
(2)代:将一组对应的x,y的值代入反比例函数的表达式,确定k的值.
(3)写:写出反比例函数的表达式.如图,在平面直角坐
标系中,直线 与x轴交于点A,与双
曲线y= 在第一象限内交于点B,BC⊥x轴于
点C,OC=2AO,求双曲线的表达式.【解析】∵直线
∴A(-1,0),∴OA =1.
∵OC=2OA,∴OC =2.
令x=2,得:
又∵B在双曲线上,
∴k =3.∴双曲线的表达式为 主题3 反比例函数的应用
【主题训练3】某地资源总量Q一定,该地人均资源享有量 与人口数n的函数关系图象是 ( )【自主解答】选B.根据资源总量Q=人均资源享有量 ×人口数
n得, 其中Q是常量且Q>0得 与n成反比例函数关系,图
象为其在第一象限的部分.【主题升华】
用反比例函数解决实际问题“四步法”
(1)分析题意:找出问题中的常量、变量(有时常量、变量以图象的形式给出),并且理清常量与变量之间的关系.
(2)设关系式:根据常量与变量之间的关系,设出反比例函数关系式.
(3)求解系数:利用待定系数法确定反比例函数关系式.
(4)确定答案:根据反比例函数的图象与性质解决实际问题.【备选例题】已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式.
(2)观察图象,当x>0时,直接写出y1>y2时自变量x的取值范围.
(3)如果点C与点A关于x轴对称,求△ABC的面积.【自主解答】(1)∵函数y1= 的图象过点A(1,4),
即4= ,∴k=4,即y1= .
又∵点B(m,-2)在y1= 上,
∴m=-2,∴B(-2,-2).
又∵一次函数y2=ax+b过A,B两点,
即
∴y2=2x+2.
综上可得y1= ,y2=2x+2.(2)当x>0时,要使y1>y2,即函数y1的图象总在函数y2的图象上方,
∴0
∴C(1,-4).
过点B作BD⊥AC,垂足为D,如图,则D(1,-2),
于是△ABC的高BD=1-(-2)=3,
底为AC=4-(-4)=8.
∴S△ABC= AC·BD= ×8×3=12.1.已知矩形的面积为36cm2,相邻两条边长分别为xcm和ycm,则y与x之间的函数图象大致是 ( )【解析】选A.依题意,xy=36,∴y= ,其图象为位于一、三象
限的双曲线.又∵矩形边长x>0,所以图象为第一象限的一个分
支,且y随x的增大而减小.2.为了更好保护水资源,造福人类.某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:V = Sh(V≠0),则S关于h的函数图象大致是 ( )【解析】选C.∵V = Sh(V≠0,其中V为常量),∴S= (h>0),则
S关于h的函数图象是双曲线在第一象限内的一部分,只有C符合.3.如图,等边三角形ABC放置在平面直角坐标系中,已知A(0,0),B(6,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的关系式.
(2)将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.【解析】(1)过点C作CH⊥x轴,垂足为H.∵△ABC是等边三角形,∴AH= AB=3,∴
设反比例函数的关系式为
即 (2)∵将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,∴设此时的点B坐标为(6,n),∴6n=9 ,解得n=
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
