六年级下册数学习题课件-3圆柱和圆锥-圆柱-人教版(共18张PPT)
文档属性
| 名称 | 六年级下册数学习题课件-3圆柱和圆锥-圆柱-人教版(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
人教版六年级下册《数学》
主题一:圆柱的表面积计算公式推导?
1.圆柱表面积是指 (说说你的理解)
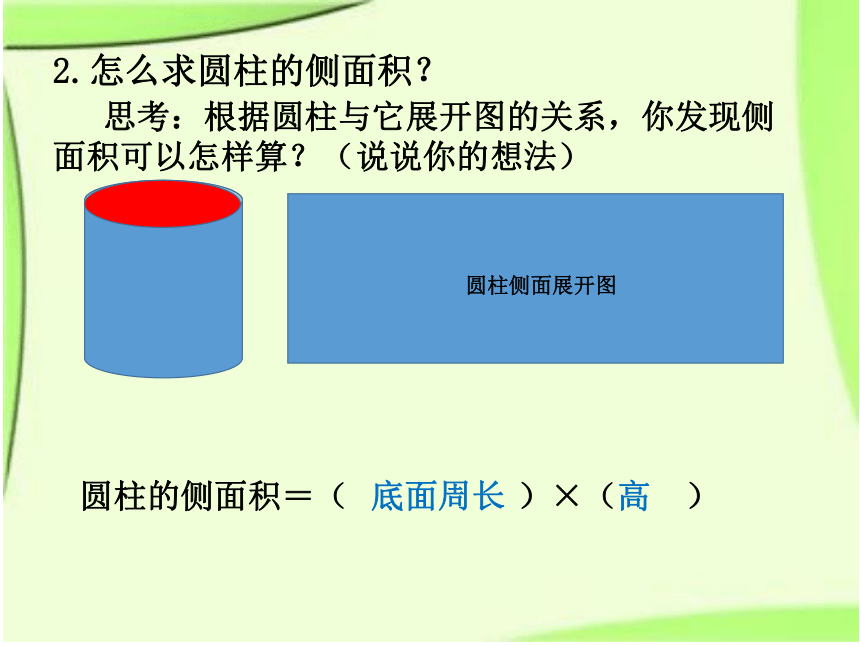
2.怎么求圆柱的侧面积?
圆柱侧面展开图
圆柱的侧面积=( )×( )
思考:根据圆柱与它展开图的关系,你发现侧面积可以怎样算?(说说你的想法)
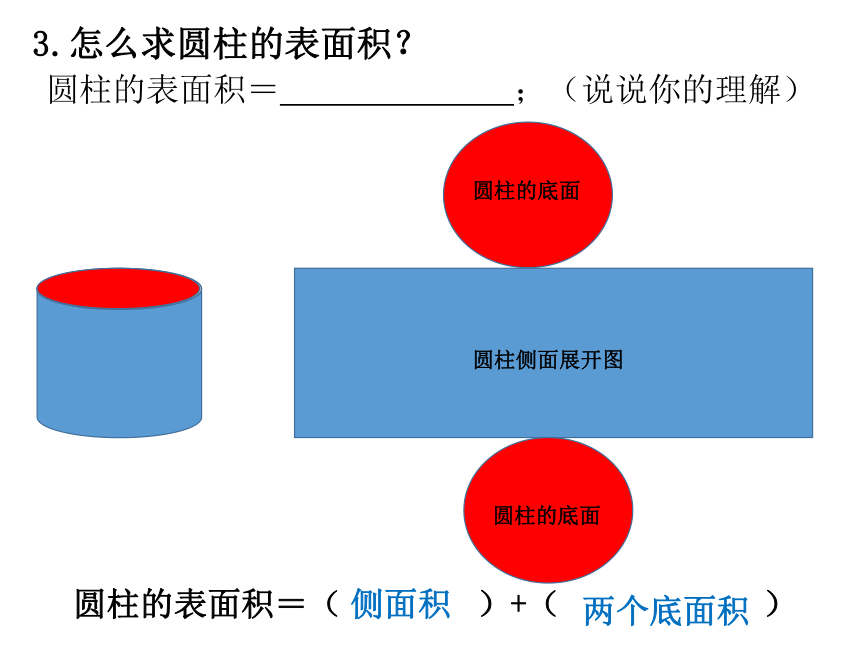
3.怎么求圆柱的表面积?
圆柱的表面积=( )+( )
圆柱的表面积= ;(说说你的理解)
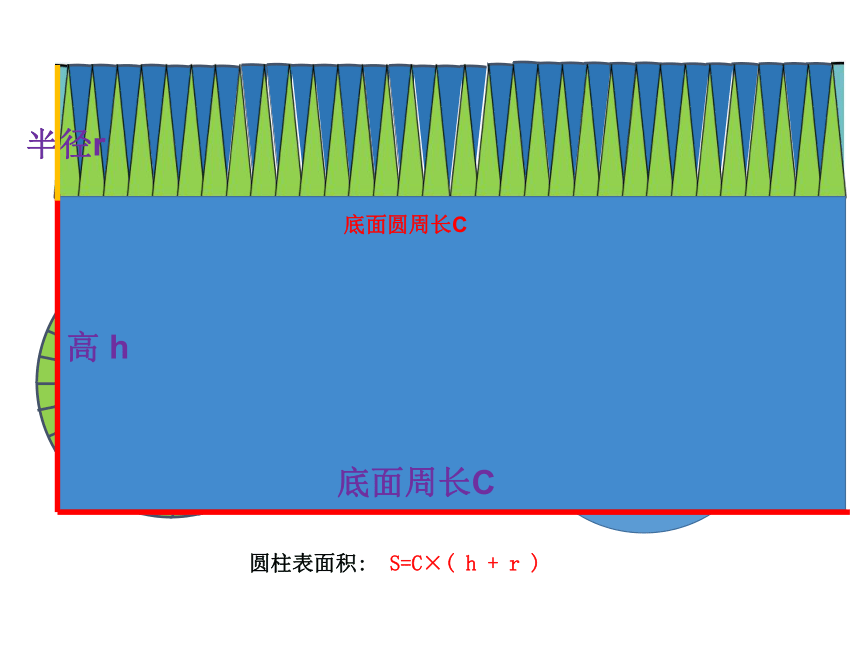
S表=S侧+2S底 =ch+2πr2 =2πrh+2πr×r =C×( + )
h
r
底面圆周长C
高 h
半径r
底面周长C
圆柱表面积: S=C×( h + r )
主题二:圆柱的表面积计算
1.一个圆柱形茶叶筒的侧面围着商标纸,它的底面半径5厘米,高30厘米,这张商标纸的面积是多少?
s=ch
=2πrh
=2×3.14×5×30
=942(cm2)
答:这张商标纸的面积是942cm2。
2.一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
说一说:你是怎么理解用“进一法”取近似值的?
(1)帽子的侧面积:
3.14×20×30=1884(cm2)
(2)帽顶的面积:
3.14×(20÷2)2=314(cm2)
(3)需要用的面料:
1884+314=2198≈2200(cm2)
答:做这样帽子至少要用2200cm2的面料。
思考:还有不一样的解题思路吗?
1.基础题
(1)小明利用废旧圆柱体纸盒做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要多少平方厘米的彩纸?(得数保留整数)
实践应用,反馈纠正:
(1)侧面积:3.14×8×13=326.56(cm2)
(2)底面积:3.14×(8÷2)2=50.24(cm2)
(3)需要用的彩纸:
326.56+50.24≈377(cm2)
答:至少要用377cm2的彩纸。
(2)一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。前轮转动一周,压路面积是多少平方米?(温馨提示:求的是什么?)
3.14×2×1.2=7.536(m2)
答:压路的面积是7.536m2。
一顶帖子(如下图),上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多?(单位:cm)
2.提高题
(1)黑布面积:
3.14×(20÷2)2+3.14×20×10=942(cm2)
(2)红布面积:
20÷2=10(cm) 10+10=20(cm)
3.14×(202-102)=942(cm2)
(3)红布与黑布面积大小比较:
942=942
答:红布与黑布多的同样多。
小明想用一张长18.84厘米,宽12.56厘米的长方形做侧面(接头处不计),制作了一个圆柱形饼干盒,这个饼干盒的表面积有多大?(得数保留整数)
3.发展题
方案一:
(1)侧面积:18.84×12.56=236.6304(cm2)
(2)底面积:3.14×(18.84÷3.14÷2)2×2=56.52(cm2)
(3)表面积:
236.6304+56.52≈294(cm2)
答:这个饼干盒的表面积约294cm2。
小明想用一张长18.84厘米,宽12.56厘米的长方形做侧面(接头处不计),制作了一个圆柱形饼干盒,这个饼干盒的表面积有多大?(得数保留整数)
3.发展题
方案二:
(1)侧面积:18.84×12.56=236.6304(cm2)
(2)底面积:3.14×(12.56÷3.14÷2)2×2=12.56(cm2)
(3)表面积:
236.6304+12.56≈250(cm2)
答:这个饼干盒的表面积约250cm2。
比较两个方案,你发现侧面积相等的圆柱,高越大,表面积越( )。
思考:你还有不一样的解题思路吗?
2.一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
底面周长
创新:
高
思考:制作只有一个底面的圆柱所需的材料面积:S=C×( h + )
移动改变视野,
转化生成智慧!
再见!
人教版六年级下册《数学》
主题一:圆柱的表面积计算公式推导?
1.圆柱表面积是指 (说说你的理解)
2.怎么求圆柱的侧面积?
圆柱侧面展开图
圆柱的侧面积=( )×( )
思考:根据圆柱与它展开图的关系,你发现侧面积可以怎样算?(说说你的想法)
3.怎么求圆柱的表面积?
圆柱的表面积=( )+( )
圆柱的表面积= ;(说说你的理解)
S表=S侧+2S底 =ch+2πr2 =2πrh+2πr×r =C×( + )
h
r
底面圆周长C
高 h
半径r
底面周长C
圆柱表面积: S=C×( h + r )
主题二:圆柱的表面积计算
1.一个圆柱形茶叶筒的侧面围着商标纸,它的底面半径5厘米,高30厘米,这张商标纸的面积是多少?
s=ch
=2πrh
=2×3.14×5×30
=942(cm2)
答:这张商标纸的面积是942cm2。
2.一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
说一说:你是怎么理解用“进一法”取近似值的?
(1)帽子的侧面积:
3.14×20×30=1884(cm2)
(2)帽顶的面积:
3.14×(20÷2)2=314(cm2)
(3)需要用的面料:
1884+314=2198≈2200(cm2)
答:做这样帽子至少要用2200cm2的面料。
思考:还有不一样的解题思路吗?
1.基础题
(1)小明利用废旧圆柱体纸盒做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要多少平方厘米的彩纸?(得数保留整数)
实践应用,反馈纠正:
(1)侧面积:3.14×8×13=326.56(cm2)
(2)底面积:3.14×(8÷2)2=50.24(cm2)
(3)需要用的彩纸:
326.56+50.24≈377(cm2)
答:至少要用377cm2的彩纸。
(2)一台压路机的前轮是圆柱形,轮宽2米,直径1.2米。前轮转动一周,压路面积是多少平方米?(温馨提示:求的是什么?)
3.14×2×1.2=7.536(m2)
答:压路的面积是7.536m2。
一顶帖子(如下图),上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多?(单位:cm)
2.提高题
(1)黑布面积:
3.14×(20÷2)2+3.14×20×10=942(cm2)
(2)红布面积:
20÷2=10(cm) 10+10=20(cm)
3.14×(202-102)=942(cm2)
(3)红布与黑布面积大小比较:
942=942
答:红布与黑布多的同样多。
小明想用一张长18.84厘米,宽12.56厘米的长方形做侧面(接头处不计),制作了一个圆柱形饼干盒,这个饼干盒的表面积有多大?(得数保留整数)
3.发展题
方案一:
(1)侧面积:18.84×12.56=236.6304(cm2)
(2)底面积:3.14×(18.84÷3.14÷2)2×2=56.52(cm2)
(3)表面积:
236.6304+56.52≈294(cm2)
答:这个饼干盒的表面积约294cm2。
小明想用一张长18.84厘米,宽12.56厘米的长方形做侧面(接头处不计),制作了一个圆柱形饼干盒,这个饼干盒的表面积有多大?(得数保留整数)
3.发展题
方案二:
(1)侧面积:18.84×12.56=236.6304(cm2)
(2)底面积:3.14×(12.56÷3.14÷2)2×2=12.56(cm2)
(3)表面积:
236.6304+12.56≈250(cm2)
答:这个饼干盒的表面积约250cm2。
比较两个方案,你发现侧面积相等的圆柱,高越大,表面积越( )。
思考:你还有不一样的解题思路吗?
2.一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
底面周长
创新:
高
思考:制作只有一个底面的圆柱所需的材料面积:S=C×( h + )
移动改变视野,
转化生成智慧!
再见!
