人教A版高中数学 选修2-2 第一章 1.5.2汽车行驶的路程 课件(共35张PPT)
文档属性
| 名称 | 人教A版高中数学 选修2-2 第一章 1.5.2汽车行驶的路程 课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
定积分:以直代曲,用“均匀”的研究“不均匀”的;用无限的方法研究有限的问题,从局部到整体
具体实例:曲边梯形的面积、变速直线运动的路程
1.5 定积分的概念
新课导入
中学学习过:三角形,圆形,矩形,平行四边形,梯形等规则图形面积的计算,而计算平面曲线围成的平面“曲边图形”的面积、变速直线运动物体位移、变力做功等问题.
我们已学过了如何计算曲边图形面积.
如何计算变速
直线物体位移呢?
利用导数我们解决了“已知物体运动路程与时间的关系,求物体运动速度”的问题.反之,如果已知物体的速度与时间的关系,如何求其在一定时间内经过的路程?
提出问题
1.5.2 汽车行驶的路程
教学目标
知识与能力
“以不变代变”的方法,把变速直线运动的路程问题化归为匀速直线运动的路程问题,凭借求曲边梯形的经验解决问题.
过程与方法
(1)结合求曲线梯形面积化为四个步骤:分割、近似代替、求和、取极限分析汽车变速直线运动.
(2)了解定积分概念中蕴涵的最本质的思想.
情感态度与价值观
本节通过实例加深同学对“以不变代变”“分割”“以局部代整体”等积分思想的理解.
教学重难点
重点
结合上节知识解决汽车变速直线运动的问题.
难点
以“不变代变”的思想方法,定积分的概念.
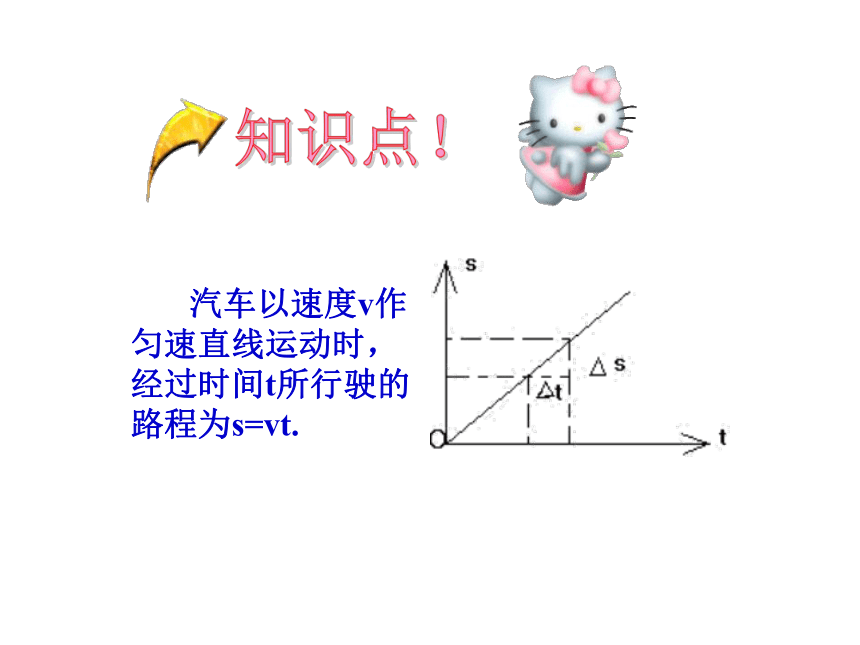
汽车以速度v作匀速直线运动时,经过时间t所行驶的路程为s=vt.
知识点!
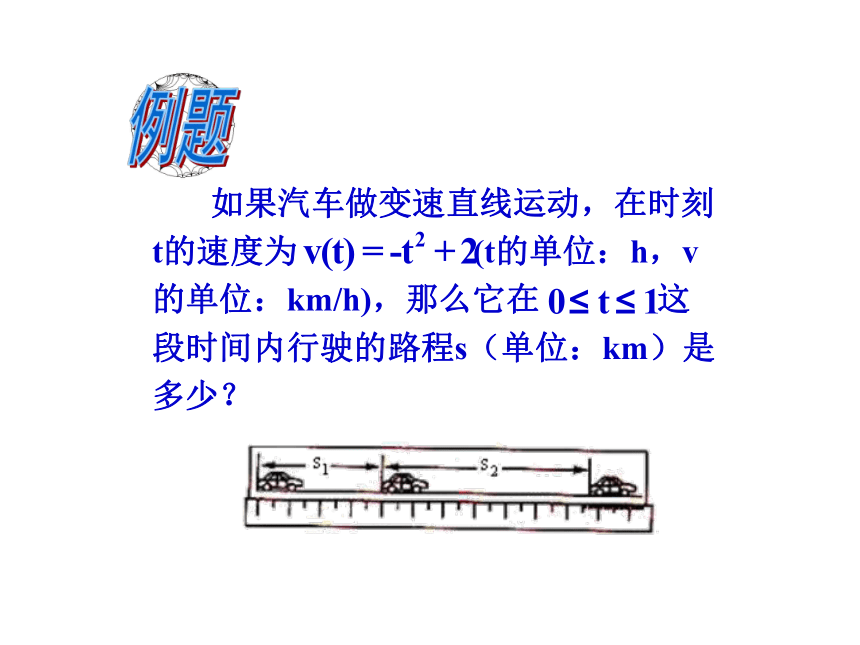
例题
如果汽车做变速直线运动,在时刻t的速度为 (t的单位:h,v的单位:km/h),那么它在 这段时间内行驶的路程s(单位:km)是多少?
思考?
与求曲边梯形面积相似,我们采取“以不变代变”的方法,把求变速直线运动的路程问题,化归为求匀速直线运动的路程问题.
将区间[0,1]等分成n个小区间,在每个小区间上.由于v(t)的变化很小.
可以认为汽车近似做匀速直线运动,从而求得汽车在每个小区间上行驶路程的近似值,再求和得s的近似值,最后让n趋向于无穷大就得到s的精确值.
思路
分割:
在时间区间[0,1]上等间隔地插入n-1个分点,将它等分成n个小区间:
记第i个区间为 ,其长度为:
把汽车在时间段 上行驶的路程分别记作:
显然有
近似代替:
当n很大,即 很小时,在区间 上,函数 的变化值很小,近似地等于一个常数.
从物理意义上看,就是汽车在时间段 上的速度变化很小,不妨认为它近似地以时刻 处的速度作匀速行驶.
在区间 上,近似地认为 即在局部小范围内认为“以匀速代变速”.
由近似代替求得:
求和:
取极限:
当n趋向于无穷大,即 趋向于0时, 趋向于s,从而有
结合求曲线梯形面积的过程,你认为汽车行驶的路程s和由直线t=0,t=1,v=0和曲线 所围成的曲边梯形的面积有什么关系?
由于 在数值上等于下图所有小矩形的面积之和.其极限就是由直线t=0,t=1,v=0和曲线 所围成的曲边梯形的面积,从而汽车行驶的路程在数值上等于由直线t=0,t=1,v=0和曲线 所围成的曲边梯形的面积.
. . .
一般地,如果物体做变速直线运动,速度函数为 ,那么我们也可以采用分割、近似代替、求和、取极限的方法,求出它在 内的位移s.
我想到了
单位时间通过的路程
例题1
小王驱车到80km外的一个小镇,共用了2个小时, (km/h)为汽车行驶的平均速度,然而车速器显示的速度(瞬时速度)却在不停地变化,因为汽车作的是变速运动,如何计算汽车行驶的瞬时速度呢?
一般地:
设S是某一物体从某一选定时刻到时刻t 所走过的路程,则S是t 的一个函数
下面讨论物体在任一时刻t0 的瞬时速度.
瞬时速度
内的平均速度为
很小时,速度的变化不大,可以以匀速代替.
越小,平均速度 就越接近于时刻 的瞬时速度令 取极限, 得到瞬时速度
局部以匀速代替变速,以平均速度代替瞬时速度,然后通过取极限,从瞬时速度的近似值过渡到瞬时速度的精确值.
一小球做自由落体运动,其运动方程为
研究
例题2
考察小球在 s 时的瞬时速度 .
…
[1.5,2]
[1.99,2]
[1.9999,2]
0.5
0.01
0.0001
…
17.150
19.551
19.600
2
0
19.6
[2,2.001]
0.001
19.605
[2,2.01]
0.01
19.649
22.050
0.5
[2,2.5]
其变化情况见下表 :
从表上可以看出,不同时间段上的平均速度不相等,当时间段 很小时,平均速度 很接近某一确定的值19.6 (m/s),即小球在 s时的瞬时速度为:
你能用学过的知识计算出来吗?
相关实例
(1)分割
(3)求和
(4)取极限
(2)取近似
课堂小结
若做为整体来看,物体做变速直线运动,求路程. 没有现成公式,与上例类似,把时间间隔分成若干小段,在每一小段时间间隔内,近似地认为速度不变,用匀速直线运动代替,求出各小段的路程再相加,得到路程的近似值,最后通过对时间的无限细分求得路程的精确值.
课堂练习
设汽缸内活塞一侧存有定量气体,气体做等温膨胀时推动活塞向右移动一段距离,若气体体积由 变至 ,求气体压力所做的功(如下图).
气体膨胀为等温过程,所以气体压强为 ( —气体体积, —常数),而活塞上的总压力为 :
课堂答案
( —活塞的截面积, 为活塞移动的距离,)以 与 表示活塞的初始与终止位置,于是得功为
定积分:以直代曲,用“均匀”的研究“不均匀”的;用无限的方法研究有限的问题,从局部到整体
具体实例:曲边梯形的面积、变速直线运动的路程
1.5 定积分的概念
新课导入
中学学习过:三角形,圆形,矩形,平行四边形,梯形等规则图形面积的计算,而计算平面曲线围成的平面“曲边图形”的面积、变速直线运动物体位移、变力做功等问题.
我们已学过了如何计算曲边图形面积.
如何计算变速
直线物体位移呢?
利用导数我们解决了“已知物体运动路程与时间的关系,求物体运动速度”的问题.反之,如果已知物体的速度与时间的关系,如何求其在一定时间内经过的路程?
提出问题
1.5.2 汽车行驶的路程
教学目标
知识与能力
“以不变代变”的方法,把变速直线运动的路程问题化归为匀速直线运动的路程问题,凭借求曲边梯形的经验解决问题.
过程与方法
(1)结合求曲线梯形面积化为四个步骤:分割、近似代替、求和、取极限分析汽车变速直线运动.
(2)了解定积分概念中蕴涵的最本质的思想.
情感态度与价值观
本节通过实例加深同学对“以不变代变”“分割”“以局部代整体”等积分思想的理解.
教学重难点
重点
结合上节知识解决汽车变速直线运动的问题.
难点
以“不变代变”的思想方法,定积分的概念.
汽车以速度v作匀速直线运动时,经过时间t所行驶的路程为s=vt.
知识点!
例题
如果汽车做变速直线运动,在时刻t的速度为 (t的单位:h,v的单位:km/h),那么它在 这段时间内行驶的路程s(单位:km)是多少?
思考?
与求曲边梯形面积相似,我们采取“以不变代变”的方法,把求变速直线运动的路程问题,化归为求匀速直线运动的路程问题.
将区间[0,1]等分成n个小区间,在每个小区间上.由于v(t)的变化很小.
可以认为汽车近似做匀速直线运动,从而求得汽车在每个小区间上行驶路程的近似值,再求和得s的近似值,最后让n趋向于无穷大就得到s的精确值.
思路
分割:
在时间区间[0,1]上等间隔地插入n-1个分点,将它等分成n个小区间:
记第i个区间为 ,其长度为:
把汽车在时间段 上行驶的路程分别记作:
显然有
近似代替:
当n很大,即 很小时,在区间 上,函数 的变化值很小,近似地等于一个常数.
从物理意义上看,就是汽车在时间段 上的速度变化很小,不妨认为它近似地以时刻 处的速度作匀速行驶.
在区间 上,近似地认为 即在局部小范围内认为“以匀速代变速”.
由近似代替求得:
求和:
取极限:
当n趋向于无穷大,即 趋向于0时, 趋向于s,从而有
结合求曲线梯形面积的过程,你认为汽车行驶的路程s和由直线t=0,t=1,v=0和曲线 所围成的曲边梯形的面积有什么关系?
由于 在数值上等于下图所有小矩形的面积之和.其极限就是由直线t=0,t=1,v=0和曲线 所围成的曲边梯形的面积,从而汽车行驶的路程在数值上等于由直线t=0,t=1,v=0和曲线 所围成的曲边梯形的面积.
. . .
一般地,如果物体做变速直线运动,速度函数为 ,那么我们也可以采用分割、近似代替、求和、取极限的方法,求出它在 内的位移s.
我想到了
单位时间通过的路程
例题1
小王驱车到80km外的一个小镇,共用了2个小时, (km/h)为汽车行驶的平均速度,然而车速器显示的速度(瞬时速度)却在不停地变化,因为汽车作的是变速运动,如何计算汽车行驶的瞬时速度呢?
一般地:
设S是某一物体从某一选定时刻到时刻t 所走过的路程,则S是t 的一个函数
下面讨论物体在任一时刻t0 的瞬时速度.
瞬时速度
内的平均速度为
很小时,速度的变化不大,可以以匀速代替.
越小,平均速度 就越接近于时刻 的瞬时速度令 取极限, 得到瞬时速度
局部以匀速代替变速,以平均速度代替瞬时速度,然后通过取极限,从瞬时速度的近似值过渡到瞬时速度的精确值.
一小球做自由落体运动,其运动方程为
研究
例题2
考察小球在 s 时的瞬时速度 .
…
[1.5,2]
[1.99,2]
[1.9999,2]
0.5
0.01
0.0001
…
17.150
19.551
19.600
2
0
19.6
[2,2.001]
0.001
19.605
[2,2.01]
0.01
19.649
22.050
0.5
[2,2.5]
其变化情况见下表 :
从表上可以看出,不同时间段上的平均速度不相等,当时间段 很小时,平均速度 很接近某一确定的值19.6 (m/s),即小球在 s时的瞬时速度为:
你能用学过的知识计算出来吗?
相关实例
(1)分割
(3)求和
(4)取极限
(2)取近似
课堂小结
若做为整体来看,物体做变速直线运动,求路程. 没有现成公式,与上例类似,把时间间隔分成若干小段,在每一小段时间间隔内,近似地认为速度不变,用匀速直线运动代替,求出各小段的路程再相加,得到路程的近似值,最后通过对时间的无限细分求得路程的精确值.
课堂练习
设汽缸内活塞一侧存有定量气体,气体做等温膨胀时推动活塞向右移动一段距离,若气体体积由 变至 ,求气体压力所做的功(如下图).
气体膨胀为等温过程,所以气体压强为 ( —气体体积, —常数),而活塞上的总压力为 :
课堂答案
( —活塞的截面积, 为活塞移动的距离,)以 与 表示活塞的初始与终止位置,于是得功为
