2020北师版九上数学第三章概率的进一步认识阶段复习习题课件(35张PPT)
文档属性
| 名称 | 2020北师版九上数学第三章概率的进一步认识阶段复习习题课件(35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 19:42:10 | ||
图片预览









文档简介
课件35张PPT。阶段复习课
第 三 章主题1 概率的求法
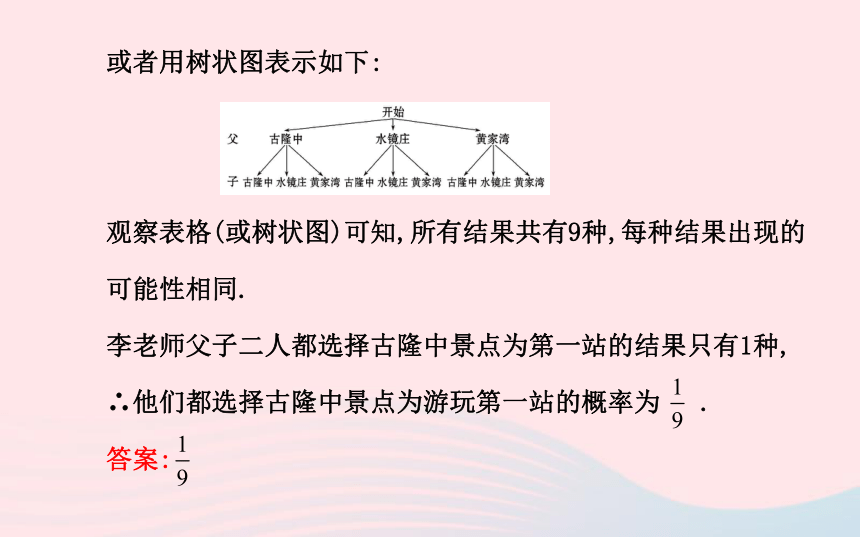
【主题训练1】襄阳市辖区内旅游景点较多.李老师和刚初中毕业的儿子准备到古隆中、水镜庄、黄家湾三个景点去游玩.如果他们各自在三个景点中任选一个作为游玩的第一站(每个景点被选为第一站的可能性相同),那么他们都选择古隆中景点为第一站的概率是 .【自主解答】根据题意,李老师父子二人选择游玩第一站的所有的结果可列表如下:或者用树状图表示如下:
观察表格(或树状图)可知,所有结果共有9种,每种结果出现的可能性相同.
李老师父子二人都选择古隆中景点为第一站的结果只有1种,
∴他们都选择古隆中景点为游玩第一站的概率为 .
答案:【主题升华】概率的常见求解类型及求法
(1)有限等可能性事件:可以通过列举所有的情况,代入概率的公式进行计算,列举的方法有列表法和画树状图法.
(2)无限等可能性事件:一般与面积、时间等有关,可以通过区域面积与总面积关系转化为有限等可能性事件来求解.
(3)发生的可能性不相等事件:用频率估计概率.1.一个布袋里装有6个只有颜色可以不同的球,其中2个红球,4个白球.从布袋里任意摸出1个球,则摸出的球是红球的概率为 ( )
【解析】选D.布袋里装有6个球,其中2个红球,摸出的球是红球的概率为 2.假定鸟卵孵化后,雏鸟为雌与雄的概率相同.如果三枚卵全部成功孵化,则三只雏鸟中有两只雌鸟的概率是 ( )
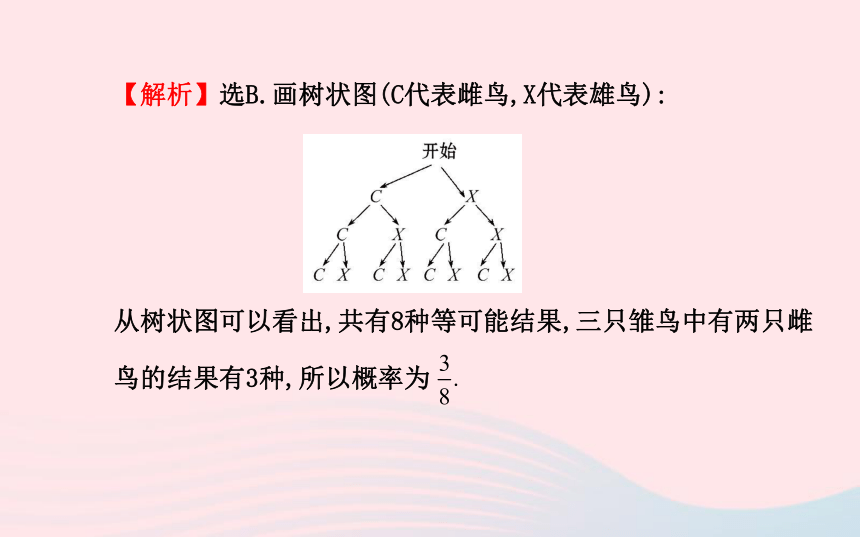
【解析】选B.画树状图(C代表雌鸟,X代表雄鸟):
从树状图可以看出,共有8种等可能结果,三只雏鸟中有两只雌鸟的结果有3种,所以概率为 3.经过某处路口的汽车,它可能继续直行或向右转,若两种可能性大小相同,则两辆汽车经过该路口全部直行的概率为 .【解析】列表得:
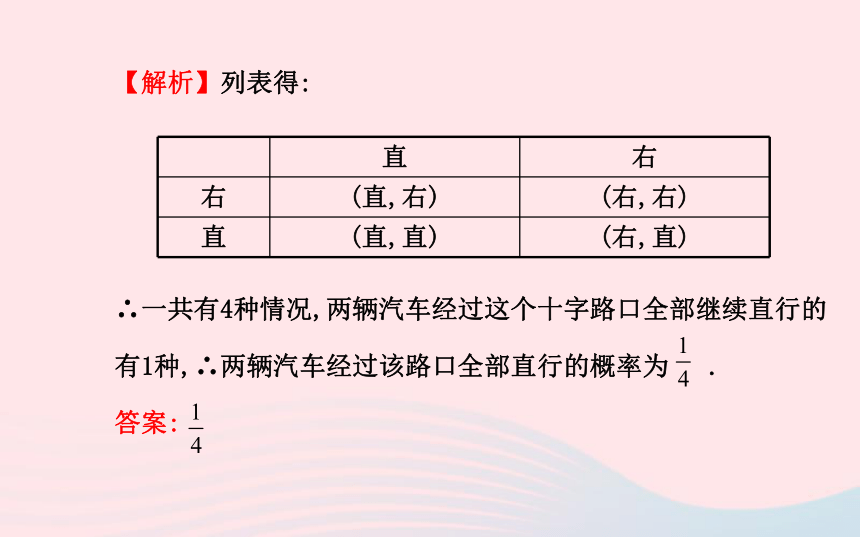
∴一共有4种情况,两辆汽车经过这个十字路口全部继续直行的有1种,∴两辆汽车经过该路口全部直行的概率为 .
答案:4.从1,2,3,4中任取一个数作为十位上的数字,再从2,3,4中任取一个数作为个位上的数字,那么组成的两位数是3的倍数的概率是 .【解析】用列表法列举所有可能结果.
共有12种等可能结果,其中12,42,33,24是3的倍数,故组成的两位数是3的倍数的概率为 .
答案:5.在-1,3,-2这三个数中,任选两个数的积作为k的值,使反比例函数y= 的图象在第一、三象限的概率是 .【解析】画树状图得:
∵共有6种等可能的结果,任选两个数的积作为k的值,使反比例函数y= 的图象在第一、三象限的有2种情况,
∴任选两个数的积作为k的值,使反比例函数y= 的图象在第一、三象限的概率是
答案:主题2 概率的应用
【主题训练2】甲、乙两位同学玩摸球游戏,准备了甲、乙两个口袋,其中甲口袋中放有标号为1,2,3,4,5的5个球,乙口袋中放有标号为1,2,3,4的4个球.游戏规则:甲从甲口袋摸一球,乙从乙口袋摸一球,摸出的两球所标数字之差(甲数字-乙数字)大于0时甲胜,小于0时乙胜,等于0时平局.你认为这个游戏规则对双方公平吗?请说明理由.若不公平,请你对本游戏设计一个对双方都公平的游戏规则.【解析】不公平.理由如下:由表可知:甲摸得数字与乙摸得数字之差大于0的有10种情况,
小于0的有6种情况,等于0的有4种情况,一共有20种等可能情况.
故P(甲胜)= P(乙胜)= P(甲)> P(乙)
∴这个游戏规则不公平.
游戏规则改为:甲、乙数字之差大于0甲胜,小于等于0乙胜,此
时P(甲)=P(乙)= .【备选例题】某中学举行“中国梦·我的梦”演讲比赛.志远班的班长和学习委员都想去,于是老师制作了四张标有算式的卡片,背面朝上洗匀后,先由班长抽一张,再由学习委员在余下三张中抽一张.如果两张卡片上的算式都正确,班长去;如果两张卡片上的算式都错误,学习委员去;如果两张卡片上的算式一个正确一个错误,则都放回去,背面朝上洗匀后再抽.这个游戏公平吗?请用树状图或列表的方法,结合概率予以说明.【解析】列表得:
一共有12种情况,设班长去的概率为P1,满足班长去的情况有2
种.所以P1= ;同理,学习委员去的概率也为 .因此此游戏
公平.【主题升华】游戏公平性的判断与解决方法
(1)游戏对双方是否公平,取决于双方获胜的概率是否相同,若相等,则游戏对双方公平,若不相等,则游戏对双方不公平.
(2)使游戏由不公平变为公平有两个途径.
①改变游戏规则,使双方获胜的概率相等.
②不改变双方的概率,改变得分情况,使双方获得的分数相等.1.把分别标有数字2,3,4,5的四个小球放入A袋内,把分别标有数字 的五个小球放入B袋内,所有小球的形状、大小、质地完全相同,A,B两个袋子不透明.
(1)小明分别从A,B两个袋子中各摸出一个小球,求这两个球上的数字互为倒数的概率.
(2)当B袋中标有 的小球上的数字变为 时(填写所有结果),(1)中的概率为 .【解析】(1)列表如下:由表可知,所有可能出现的结果共有20种,它们出现的可能性相同,其中两个球上的数字互为倒数的有4种,所以P(两个球上的数字互为倒数)=
(2) 2.某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其他均相同)打乱顺序重新排列,从中任意抽取1张卡片.
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率.(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由.
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的.【解析】(1)是20的倍数或能整除20的数有7个,则P= .
(2)不公平,无论k取何值,都能被1整除,则序号为1的学生被抽
中的概率为1,即100%,而很明显,其他学生被抽中概率不为100%.
(3)先抽出一张,记下数字,然后放回.若下一次抽到的数字与之
前抽到过的重复,则不记数,放回,重新抽取.不断重复,直至抽
满10个不同的数字为止.(这样每个数字被抽到的概率都是 )主题3 试验频率与理论概率的关系
【主题训练3】在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别.摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则估计盒子中大约有白球 ( )
A.12个 B.16个 C.20个 D.30个【自主解答】选A.设白球有x个,根据题意,得4∶(4+x)=10∶40.解得x=12.【主题升华】频率与概率的关系及应用
1.关系:当试验次数很大时,随机事件出现的频率稳定在概率这个值附近.
2.应用:根据试验的频率稳定于事件发生的概率可以估计未知量,并同时通过抽样调查利用样本估计总体的思想解决实际问题,主要是利用样本的平均数去估计总体的数量,从而解决生活中相关的实际问题.1.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放归鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中带标记的鱼有5条,则鱼塘中估计有 条鱼.
【解析】设鱼塘中估计有x条鱼,则5∶200=30∶x,
解得:x=1200.
答案:12002.在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒子中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是 .【解析】本题考查用频率估计概率知识.由摸到红球的频率稳定于0.2,可推测摸到红球的概率是0.2,根据概率公式可得
=0.2,解得n=10.
答案:103.某林业部门统计某种幼树在一定条件下的移植成活率,结果如下表所示
根据表中数据,估计这种幼树移植成活的概率为 (精确到0.1).【解析】经过大量试验,幼树移植成活的频率稳定在0.9左右,故估计幼树移植成活的概率为0.9.
答案:0.9
第 三 章主题1 概率的求法
【主题训练1】襄阳市辖区内旅游景点较多.李老师和刚初中毕业的儿子准备到古隆中、水镜庄、黄家湾三个景点去游玩.如果他们各自在三个景点中任选一个作为游玩的第一站(每个景点被选为第一站的可能性相同),那么他们都选择古隆中景点为第一站的概率是 .【自主解答】根据题意,李老师父子二人选择游玩第一站的所有的结果可列表如下:或者用树状图表示如下:
观察表格(或树状图)可知,所有结果共有9种,每种结果出现的可能性相同.
李老师父子二人都选择古隆中景点为第一站的结果只有1种,
∴他们都选择古隆中景点为游玩第一站的概率为 .
答案:【主题升华】概率的常见求解类型及求法
(1)有限等可能性事件:可以通过列举所有的情况,代入概率的公式进行计算,列举的方法有列表法和画树状图法.
(2)无限等可能性事件:一般与面积、时间等有关,可以通过区域面积与总面积关系转化为有限等可能性事件来求解.
(3)发生的可能性不相等事件:用频率估计概率.1.一个布袋里装有6个只有颜色可以不同的球,其中2个红球,4个白球.从布袋里任意摸出1个球,则摸出的球是红球的概率为 ( )
【解析】选D.布袋里装有6个球,其中2个红球,摸出的球是红球的概率为 2.假定鸟卵孵化后,雏鸟为雌与雄的概率相同.如果三枚卵全部成功孵化,则三只雏鸟中有两只雌鸟的概率是 ( )
【解析】选B.画树状图(C代表雌鸟,X代表雄鸟):
从树状图可以看出,共有8种等可能结果,三只雏鸟中有两只雌鸟的结果有3种,所以概率为 3.经过某处路口的汽车,它可能继续直行或向右转,若两种可能性大小相同,则两辆汽车经过该路口全部直行的概率为 .【解析】列表得:
∴一共有4种情况,两辆汽车经过这个十字路口全部继续直行的有1种,∴两辆汽车经过该路口全部直行的概率为 .
答案:4.从1,2,3,4中任取一个数作为十位上的数字,再从2,3,4中任取一个数作为个位上的数字,那么组成的两位数是3的倍数的概率是 .【解析】用列表法列举所有可能结果.
共有12种等可能结果,其中12,42,33,24是3的倍数,故组成的两位数是3的倍数的概率为 .
答案:5.在-1,3,-2这三个数中,任选两个数的积作为k的值,使反比例函数y= 的图象在第一、三象限的概率是 .【解析】画树状图得:
∵共有6种等可能的结果,任选两个数的积作为k的值,使反比例函数y= 的图象在第一、三象限的有2种情况,
∴任选两个数的积作为k的值,使反比例函数y= 的图象在第一、三象限的概率是
答案:主题2 概率的应用
【主题训练2】甲、乙两位同学玩摸球游戏,准备了甲、乙两个口袋,其中甲口袋中放有标号为1,2,3,4,5的5个球,乙口袋中放有标号为1,2,3,4的4个球.游戏规则:甲从甲口袋摸一球,乙从乙口袋摸一球,摸出的两球所标数字之差(甲数字-乙数字)大于0时甲胜,小于0时乙胜,等于0时平局.你认为这个游戏规则对双方公平吗?请说明理由.若不公平,请你对本游戏设计一个对双方都公平的游戏规则.【解析】不公平.理由如下:由表可知:甲摸得数字与乙摸得数字之差大于0的有10种情况,
小于0的有6种情况,等于0的有4种情况,一共有20种等可能情况.
故P(甲胜)= P(乙胜)= P(甲)> P(乙)
∴这个游戏规则不公平.
游戏规则改为:甲、乙数字之差大于0甲胜,小于等于0乙胜,此
时P(甲)=P(乙)= .【备选例题】某中学举行“中国梦·我的梦”演讲比赛.志远班的班长和学习委员都想去,于是老师制作了四张标有算式的卡片,背面朝上洗匀后,先由班长抽一张,再由学习委员在余下三张中抽一张.如果两张卡片上的算式都正确,班长去;如果两张卡片上的算式都错误,学习委员去;如果两张卡片上的算式一个正确一个错误,则都放回去,背面朝上洗匀后再抽.这个游戏公平吗?请用树状图或列表的方法,结合概率予以说明.【解析】列表得:
一共有12种情况,设班长去的概率为P1,满足班长去的情况有2
种.所以P1= ;同理,学习委员去的概率也为 .因此此游戏
公平.【主题升华】游戏公平性的判断与解决方法
(1)游戏对双方是否公平,取决于双方获胜的概率是否相同,若相等,则游戏对双方公平,若不相等,则游戏对双方不公平.
(2)使游戏由不公平变为公平有两个途径.
①改变游戏规则,使双方获胜的概率相等.
②不改变双方的概率,改变得分情况,使双方获得的分数相等.1.把分别标有数字2,3,4,5的四个小球放入A袋内,把分别标有数字 的五个小球放入B袋内,所有小球的形状、大小、质地完全相同,A,B两个袋子不透明.
(1)小明分别从A,B两个袋子中各摸出一个小球,求这两个球上的数字互为倒数的概率.
(2)当B袋中标有 的小球上的数字变为 时(填写所有结果),(1)中的概率为 .【解析】(1)列表如下:由表可知,所有可能出现的结果共有20种,它们出现的可能性相同,其中两个球上的数字互为倒数的有4种,所以P(两个球上的数字互为倒数)=
(2) 2.某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其他均相同)打乱顺序重新排列,从中任意抽取1张卡片.
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率.(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由.
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的.【解析】(1)是20的倍数或能整除20的数有7个,则P= .
(2)不公平,无论k取何值,都能被1整除,则序号为1的学生被抽
中的概率为1,即100%,而很明显,其他学生被抽中概率不为100%.
(3)先抽出一张,记下数字,然后放回.若下一次抽到的数字与之
前抽到过的重复,则不记数,放回,重新抽取.不断重复,直至抽
满10个不同的数字为止.(这样每个数字被抽到的概率都是 )主题3 试验频率与理论概率的关系
【主题训练3】在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别.摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则估计盒子中大约有白球 ( )
A.12个 B.16个 C.20个 D.30个【自主解答】选A.设白球有x个,根据题意,得4∶(4+x)=10∶40.解得x=12.【主题升华】频率与概率的关系及应用
1.关系:当试验次数很大时,随机事件出现的频率稳定在概率这个值附近.
2.应用:根据试验的频率稳定于事件发生的概率可以估计未知量,并同时通过抽样调查利用样本估计总体的思想解决实际问题,主要是利用样本的平均数去估计总体的数量,从而解决生活中相关的实际问题.1.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放归鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中带标记的鱼有5条,则鱼塘中估计有 条鱼.
【解析】设鱼塘中估计有x条鱼,则5∶200=30∶x,
解得:x=1200.
答案:12002.在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒子中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是 .【解析】本题考查用频率估计概率知识.由摸到红球的频率稳定于0.2,可推测摸到红球的概率是0.2,根据概率公式可得
=0.2,解得n=10.
答案:103.某林业部门统计某种幼树在一定条件下的移植成活率,结果如下表所示
根据表中数据,估计这种幼树移植成活的概率为 (精确到0.1).【解析】经过大量试验,幼树移植成活的频率稳定在0.9左右,故估计幼树移植成活的概率为0.9.
答案:0.9
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
