2020北师版九上数学第四章图形的相似4.4探索三角形相似的条件第1课时习题课件(19张PPT)
文档属性
| 名称 | 2020北师版九上数学第四章图形的相似4.4探索三角形相似的条件第1课时习题课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 00:00:00 | ||
图片预览





文档简介
课件19张PPT。4 探索三角形相似的条件
第1课时1.相似三角形:
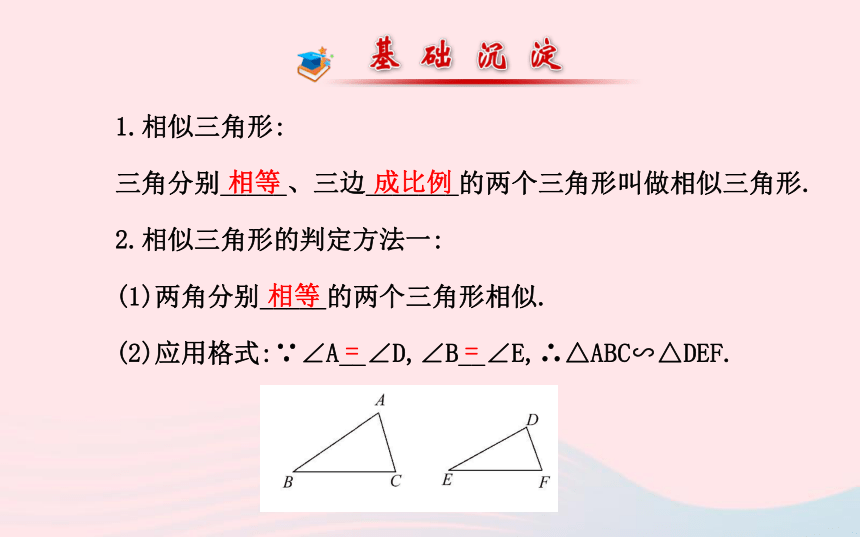
三角分别_____、三边_______的两个三角形叫做相似三角形.
2.相似三角形的判定方法一:
(1)两角分别_____的两个三角形相似.
(2)应用格式:∵∠A__∠D,∠B__∠E,∴△ABC∽△DEF.相等成比例相等==3.相似三角形的判定方法二:
(1)两边_______且夹角_____的两个三角形相似.
(2)应用格式:∵__________,∠A=∠D,∴△ABC∽△DEF.成比例相等【思维诊断】(打“√”或“×”)
1.所有的等边三角形都相似. ( )
2.两个三角形相似,它们的大小可能相等. ( )
3.有一个角对应相等的两个等腰三角形相似. ( )
4.有一个角为30°的两个直角三角形相似. ( )√√×√知识点一 应用两角相等判定三角形相似
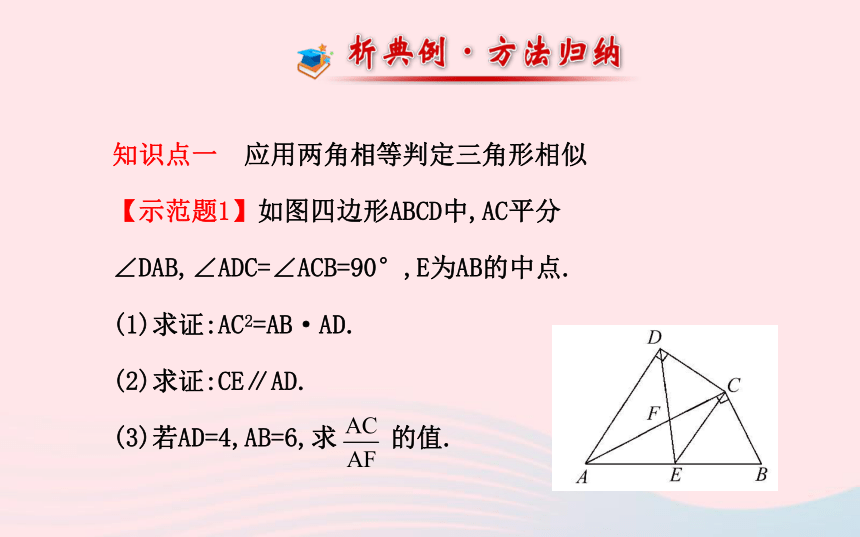
【示范题1】如图四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB·AD.
(2)求证:CE∥AD.
(3)若AD=4,AB=6,求 的值.【思路点拨】(1)已知条件→△ADC∽△ACB→AC2=AB·AD.
(2)CE=AE→∠EAC=∠ECA→∠CAD=∠ACE→CE∥AD.
(3)△AFD∽△CFE→ 【自主解答】(1)∵AC平分∠DAB,∴∠DAC=∠CAB,
又∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,
∴ ∴AC2=AB·AD.
(2)∵E为AB的中点,∴CE= AB=AE,∠EAC=∠ECA,
∵AC平分∠DAB,∴∠CAD=∠CAB,
∴∠DAC=∠ECA,∴CE∥AD.(3)∵CE∥AD,∴∠DAF=∠ECF,∠ADF=∠CEF,
∴△AFD∽△CFE,∴
∵CE= AB,∴CE= ×6=3.
又∵AD=4,由
【想一想】
利用两角分别相等判定两个等腰三角形相似,需要具备什么条件?
提示:一顶角对应相等或者一底角对应相等的两个等腰三角形相似.【微点拨】两组角对应相等:当已知条件中出现平行线、对顶角、公共角或者给出几个角的大小时,一般选用两组角对应相等的两个三角形相似进行判定.【方法一点通】
相似三角形的“三类构图”
1.平行线型(如图).2.相交线型(如图).3.旋转型(如图).知识点二 利用两边及夹角判定三角形相似
【示范题2】已知:如图,在△ABC中,CD⊥AB,BE⊥AC,连接DE,试说明:△ADE∽△ACB.【思路点拨】先证明△ABE∽△ACD,得出 再由∠A=∠A,得出△ADE∽△ACB.
【自主解答】∵CD⊥AB,BE⊥AC,∴∠AEB=∠ADC=90°,
又∵∠A=∠A,∴△ABE∽△ACD,
∴ ∴△ADE∽△ACB.【想一想】
示范题2图中还有哪些角相等?
提示:∠ADE=∠ACB,
∠AED=∠ABC,∠CEB=∠BDC.【备选例题】如图,在△ABC中,点D,E分别是△ABC的边AB,AC上的点,且AD=CE=3,AE=6,BD=15,根据以上条件,你认为∠B=∠AED吗?为什么?
【思路点拨】根据两组对应边的比相等且相应的夹角相等判定△ADE∽△ACB,根据相似的性质得到结论.【自主解答】∠B=∠AED,理由如下:
∵
且∠A为公共角,
∴△ADE∽△ACB,∴∠B=∠AED.【方法一点通】利用两边成比例且夹角相等判断三角形相似的“两点注意”
1.角:相等的角必须是两组对应边的夹角.
2.边:夹角的两边要注意对应,即长边与长边对应、短边与短边对应.
第1课时1.相似三角形:
三角分别_____、三边_______的两个三角形叫做相似三角形.
2.相似三角形的判定方法一:
(1)两角分别_____的两个三角形相似.
(2)应用格式:∵∠A__∠D,∠B__∠E,∴△ABC∽△DEF.相等成比例相等==3.相似三角形的判定方法二:
(1)两边_______且夹角_____的两个三角形相似.
(2)应用格式:∵__________,∠A=∠D,∴△ABC∽△DEF.成比例相等【思维诊断】(打“√”或“×”)
1.所有的等边三角形都相似. ( )
2.两个三角形相似,它们的大小可能相等. ( )
3.有一个角对应相等的两个等腰三角形相似. ( )
4.有一个角为30°的两个直角三角形相似. ( )√√×√知识点一 应用两角相等判定三角形相似
【示范题1】如图四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB·AD.
(2)求证:CE∥AD.
(3)若AD=4,AB=6,求 的值.【思路点拨】(1)已知条件→△ADC∽△ACB→AC2=AB·AD.
(2)CE=AE→∠EAC=∠ECA→∠CAD=∠ACE→CE∥AD.
(3)△AFD∽△CFE→ 【自主解答】(1)∵AC平分∠DAB,∴∠DAC=∠CAB,
又∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,
∴ ∴AC2=AB·AD.
(2)∵E为AB的中点,∴CE= AB=AE,∠EAC=∠ECA,
∵AC平分∠DAB,∴∠CAD=∠CAB,
∴∠DAC=∠ECA,∴CE∥AD.(3)∵CE∥AD,∴∠DAF=∠ECF,∠ADF=∠CEF,
∴△AFD∽△CFE,∴
∵CE= AB,∴CE= ×6=3.
又∵AD=4,由
【想一想】
利用两角分别相等判定两个等腰三角形相似,需要具备什么条件?
提示:一顶角对应相等或者一底角对应相等的两个等腰三角形相似.【微点拨】两组角对应相等:当已知条件中出现平行线、对顶角、公共角或者给出几个角的大小时,一般选用两组角对应相等的两个三角形相似进行判定.【方法一点通】
相似三角形的“三类构图”
1.平行线型(如图).2.相交线型(如图).3.旋转型(如图).知识点二 利用两边及夹角判定三角形相似
【示范题2】已知:如图,在△ABC中,CD⊥AB,BE⊥AC,连接DE,试说明:△ADE∽△ACB.【思路点拨】先证明△ABE∽△ACD,得出 再由∠A=∠A,得出△ADE∽△ACB.
【自主解答】∵CD⊥AB,BE⊥AC,∴∠AEB=∠ADC=90°,
又∵∠A=∠A,∴△ABE∽△ACD,
∴ ∴△ADE∽△ACB.【想一想】
示范题2图中还有哪些角相等?
提示:∠ADE=∠ACB,
∠AED=∠ABC,∠CEB=∠BDC.【备选例题】如图,在△ABC中,点D,E分别是△ABC的边AB,AC上的点,且AD=CE=3,AE=6,BD=15,根据以上条件,你认为∠B=∠AED吗?为什么?
【思路点拨】根据两组对应边的比相等且相应的夹角相等判定△ADE∽△ACB,根据相似的性质得到结论.【自主解答】∠B=∠AED,理由如下:
∵
且∠A为公共角,
∴△ADE∽△ACB,∴∠B=∠AED.【方法一点通】利用两边成比例且夹角相等判断三角形相似的“两点注意”
1.角:相等的角必须是两组对应边的夹角.
2.边:夹角的两边要注意对应,即长边与长边对应、短边与短边对应.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
