2020北师版九上数学第四章图形的相似4.4探索三角形相似的条件第2课时习题课件(16张PPT)
文档属性
| 名称 | 2020北师版九上数学第四章图形的相似4.4探索三角形相似的条件第2课时习题课件(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 19:25:13 | ||
图片预览





文档简介
课件16张PPT。4 探索三角形相似的条件
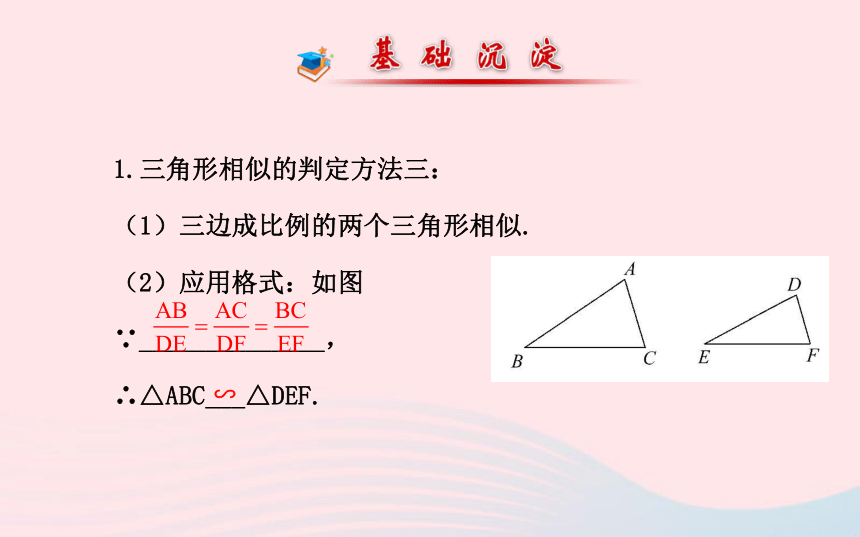
第2课时1.三角形相似的判定方法三:
(1)三边成比例的两个三角形相似.
(2)应用格式:如图
∵______________,
∴△ABC___△DEF.∽2.黄金分割:点C把线段AB分成两条线段AC和BC,如果
那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC
与AB的比叫做_______,其比值为___________.黄金比【思维诊断】(打“√”或“×”)
1.两个等腰三角形相似. ( )
2.若把△ABC各边分别扩大为原来的5倍,得到△A′B′C′,则
△ABC与△A′B′C′的各对应角相等. ( )
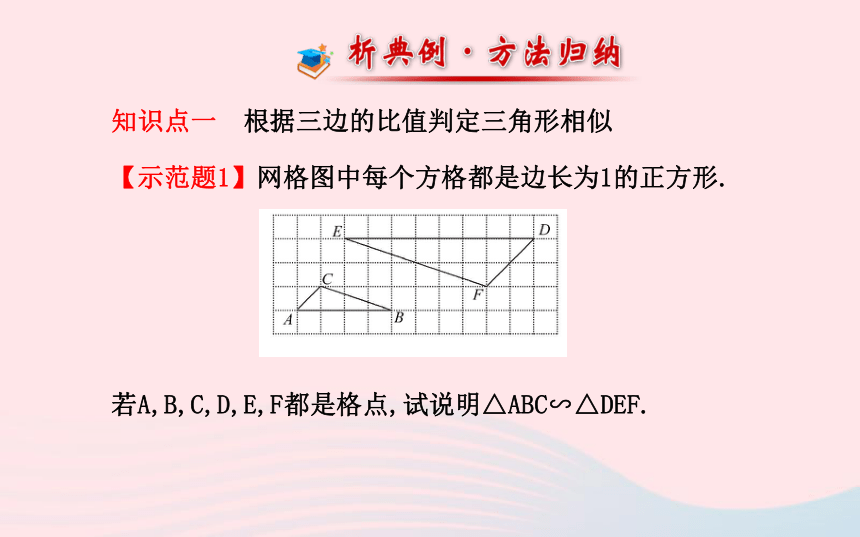
3.一条线段的黄金分割点有2个 ( ) ×√√知识点一 根据三边的比值判定三角形相似
【示范题1】网格图中每个方格都是边长为1的正方形.
若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.【思路点拨】根据勾股定理分别计算两个三角形各边的长,然后计算对应边的比,比较后作出判断.
【自主解答】在△ABC中,
AB=4,在△DEF中,
∴△ABC∽△DEF.【想一想】
格点三角形的各边长是怎样计算的?
提示:利用数格子,或将三角形的一条边看作一个直角三角形的斜边,利用勾股定理求解.【备选例题】一个三角形的三边长分别为12cm,8cm,7cm,另一个三角形的三边长分别为16cm,24cm,14cm,这两个三角形相似吗?为什么?
【解析】把两个三角形的三边按由小到大顺序排列分别为: 7cm,8cm,12cm和14cm,16cm,24cm. ∵
∴这两个三角形相似.【方法一点通】
利用三边成比例判断三角形相似的“三步骤”知识点二 黄金分割
【示范题2】已知线段AB=10cm,点C是AB的黄金分割点,且AC>BC,求AC和BC的长.【教你解题】【备选例题】为了弘扬雷锋精神,某中学准备
在校园内建造一座高2m的雷锋人体雕像,向全
体师生征集设计方案.小兵同学查阅了有关资
料,了解到黄金分割比较常用于人体雕像的设
计中,如图是小兵同学根据黄金分割比设计的雷锋人体雕像的方案,其中雷锋人体雕像下半身的高度是多少米?(精确到0.01m,参考数据: ≈2.236)【解析】根据黄金分割的定义可设雕像下半身的高度为xm,则有 整理,得x2+2x-4=0,解得x1=-1- ,
x2=-1+ ≈-1+2.236=1.236≈1.24(m).
答:雷锋人体雕像下半身的高度约是1.24m.【想一想】
若题目中没有条件AC>BC,求AC和BC的长有几种情况.
提示:有两种情况,
(1)AC>BC.
(2)AC(2)一条线段有两个黄金分割点.
(3)黄金比是一个比值,无单位.
(4)若点C是线段AB的黄金分割点(AC>BC),那么线段AC长是线段AB,BC长的比例中项.【方法一点通】
判断黄金分割的“两种方法”
1.看关系式:看所求线段中被该点分割后的三条线段是否满足:
或较长线段2=较短线段×整段线段.
2.看比值:看较短线段与较长线段的比是否是
第2课时1.三角形相似的判定方法三:
(1)三边成比例的两个三角形相似.
(2)应用格式:如图
∵______________,
∴△ABC___△DEF.∽2.黄金分割:点C把线段AB分成两条线段AC和BC,如果
那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC
与AB的比叫做_______,其比值为___________.黄金比【思维诊断】(打“√”或“×”)
1.两个等腰三角形相似. ( )
2.若把△ABC各边分别扩大为原来的5倍,得到△A′B′C′,则
△ABC与△A′B′C′的各对应角相等. ( )
3.一条线段的黄金分割点有2个 ( ) ×√√知识点一 根据三边的比值判定三角形相似
【示范题1】网格图中每个方格都是边长为1的正方形.
若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.【思路点拨】根据勾股定理分别计算两个三角形各边的长,然后计算对应边的比,比较后作出判断.
【自主解答】在△ABC中,
AB=4,在△DEF中,
∴△ABC∽△DEF.【想一想】
格点三角形的各边长是怎样计算的?
提示:利用数格子,或将三角形的一条边看作一个直角三角形的斜边,利用勾股定理求解.【备选例题】一个三角形的三边长分别为12cm,8cm,7cm,另一个三角形的三边长分别为16cm,24cm,14cm,这两个三角形相似吗?为什么?
【解析】把两个三角形的三边按由小到大顺序排列分别为: 7cm,8cm,12cm和14cm,16cm,24cm. ∵
∴这两个三角形相似.【方法一点通】
利用三边成比例判断三角形相似的“三步骤”知识点二 黄金分割
【示范题2】已知线段AB=10cm,点C是AB的黄金分割点,且AC>BC,求AC和BC的长.【教你解题】【备选例题】为了弘扬雷锋精神,某中学准备
在校园内建造一座高2m的雷锋人体雕像,向全
体师生征集设计方案.小兵同学查阅了有关资
料,了解到黄金分割比较常用于人体雕像的设
计中,如图是小兵同学根据黄金分割比设计的雷锋人体雕像的方案,其中雷锋人体雕像下半身的高度是多少米?(精确到0.01m,参考数据: ≈2.236)【解析】根据黄金分割的定义可设雕像下半身的高度为xm,则有 整理,得x2+2x-4=0,解得x1=-1- ,
x2=-1+ ≈-1+2.236=1.236≈1.24(m).
答:雷锋人体雕像下半身的高度约是1.24m.【想一想】
若题目中没有条件AC>BC,求AC和BC的长有几种情况.
提示:有两种情况,
(1)AC>BC.
(2)AC
(3)黄金比是一个比值,无单位.
(4)若点C是线段AB的黄金分割点(AC>BC),那么线段AC长是线段AB,BC长的比例中项.【方法一点通】
判断黄金分割的“两种方法”
1.看关系式:看所求线段中被该点分割后的三条线段是否满足:
或较长线段2=较短线段×整段线段.
2.看比值:看较短线段与较长线段的比是否是
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
