2020北师版九上数学第四章图形的相似4.5相似三角形判定定理的证明习题课件(17张PPT)
文档属性
| 名称 | 2020北师版九上数学第四章图形的相似4.5相似三角形判定定理的证明习题课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 00:00:00 | ||
图片预览






文档简介
课件17张PPT。﹡5
相似三角形判定定理的证明1.相似三角形的判定方法一:
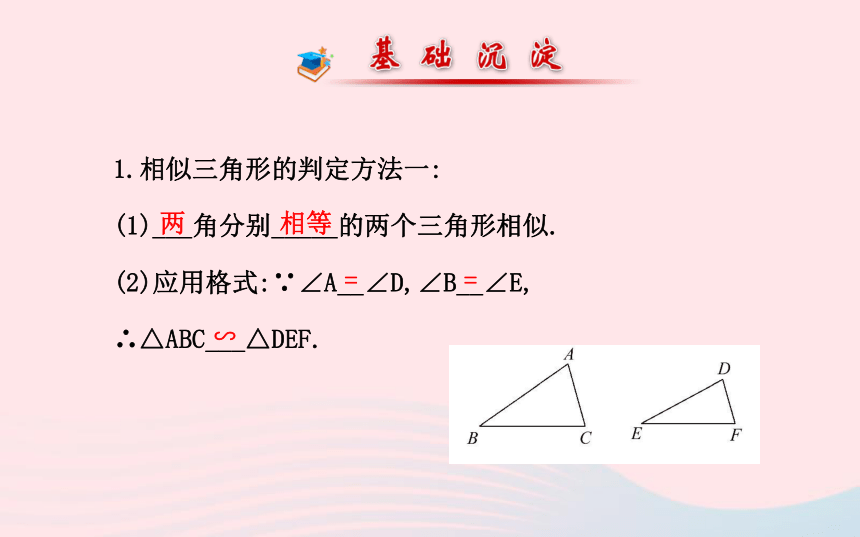
(1)___角分别_____的两个三角形相似.
(2)应用格式:∵∠A__∠D,∠B__∠E,
∴△ABC___△DEF.两相等==∽2.相似三角形的判定方法二:
(1)_____成比例且夹角_____的两个三角形相似.
(2)应用格式:__________,∠A__∠D,
∴△ABC___△DEF.两边相等=∽3.三角形相似的判定方法三:
(1)三边成比例的两个三角形相似.
(2)应用格式:∵_________________,
∴△ABC___△DEF.∽【思维诊断】(打“√”或“×”)
1.等腰直角三角形都相似. ( )
2.有一组角对应相等的两个等腰三角形相似. ( )
3.有一组角对应相等的两个直角三角形相似. ( )
4.直角三角形与该三角形中被斜边上的高分成的两个较小的直
角三角形彼此相似. ( )√××√知识点一 相似三角形的判定
【示范题1】如图,在△ABC和△ADE中,∠BAD=
∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加辅助线).
(2)请分别说明(1)中两对三角形相似的理由.
【思路点拨】∠BAD=∠CAE→∠BAC=∠DAE→△ABC∽△ADE→对应边的比相等→△ABD∽△ACE.【自主解答】(1)△ABC∽△ADE,△ABD∽△ACE.
(2)①证△ABC∽△ADE.∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.又∵∠ABC=∠ADE,
∴△ABC∽△ADE.
②证△ABD∽△ACE.
∵△ABC∽△ADE,∴
又∵∠BAD=∠CAE,∴△ABD∽△ACE.【想一想】
此题中如果已知△ABD∽△ACE,如何证明△ABC∽△ADE.
提示:∵△ABD∽△ACE,
∴∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
又∵
又∵∠BAC=∠DAE,
∴△ABC∽△ADE.【微点拨】
证明三角形相似时,需要两个条件,如果题目中出现公共角或对顶角时,需要再证明另一角相等,或者证明夹这个角的两边成比例.【方法一点通】
相似三角形的判定方法的选择
1.三边成比例:当给出的边比较多或者有边的比例关系时,选用三边成比例判定.
2.两组角相等:当出现平行线、对顶角、公共角或者给出几个角的大小时,选用两组角对应相等判定.
3.两组边对应成比例且夹角相等:当已知条件中只有一组角相等时,通过证明夹角的两边成比例判定.知识点二 相似三角形判定的综合应用
【示范题2】如图,AB=3AC,BD=3AE,又BD∥AC,点B,A,E在同一条
直线上.
(1)求证:△ABD∽△CAE.(2)如果AC=BD,AD=2 BD,设BD=a,求
BC的长.【思路点拨】
(1)证等比→证等角→得结论
(2)等量代换→求出∠D→求出∠E→求出BC
【自主解答】(1)∵AB=3AC,BD=3AE,∴
∵BD∥AC,∴∠EAC=∠DBA,∴△ABD∽△CAE.(2)连接BC,AB=3AC=3BD=3a,BD=3AE,∴AE= BD= a,
AD=2 BD=2 a,
在△ABD中,AB2=(3a)2=9a2,AD2+BD2=(2 a)2+a2=9a2,
∴AD2+BD2=AB2,∴∠D=90°,
由(1)知△ABD∽△CAE,∴∠E=∠D=90°,
在Rt△AEC中,EC2=AC2-AE2=a2-
在Rt△BEC中, 【想一想】
在示范题2(2)的条件下,连接CD,此时四边形ABDC是什么特殊的四边形?
提示:平行四边形.
∵AC∥BD,AC=BD,
∴四边形ABDC是平行四边形.【备选例题】已知四边形ABCD、四边形DCFE、四边形EFHG都是边长为1的正方形,则∠1+∠2+∠3是多少度?【解析】由题意知AC= ,CF=1,CH=2,
所以
又∠ACF=∠HCA,所以△ACF∽△HCA,
所以∠2=∠CAH,又因为∠1=∠3+∠CAH,
所以∠1+∠2+∠3=∠1+∠CAH+∠1-∠CAH=2∠1=90°.【方法一点通】
相似三角形判定的综合应用
1.在证明三角形相似时,经常要用到两种判定方法判定三角形相似,其中用一种判定方法证明三角形相似,是为另一种判定方法证明相似三角形作准备的.
2.用相似三角形的判定方法证明三角形相似时要注意几种方法综合应用.
相似三角形判定定理的证明1.相似三角形的判定方法一:
(1)___角分别_____的两个三角形相似.
(2)应用格式:∵∠A__∠D,∠B__∠E,
∴△ABC___△DEF.两相等==∽2.相似三角形的判定方法二:
(1)_____成比例且夹角_____的两个三角形相似.
(2)应用格式:__________,∠A__∠D,
∴△ABC___△DEF.两边相等=∽3.三角形相似的判定方法三:
(1)三边成比例的两个三角形相似.
(2)应用格式:∵_________________,
∴△ABC___△DEF.∽【思维诊断】(打“√”或“×”)
1.等腰直角三角形都相似. ( )
2.有一组角对应相等的两个等腰三角形相似. ( )
3.有一组角对应相等的两个直角三角形相似. ( )
4.直角三角形与该三角形中被斜边上的高分成的两个较小的直
角三角形彼此相似. ( )√××√知识点一 相似三角形的判定
【示范题1】如图,在△ABC和△ADE中,∠BAD=
∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加辅助线).
(2)请分别说明(1)中两对三角形相似的理由.
【思路点拨】∠BAD=∠CAE→∠BAC=∠DAE→△ABC∽△ADE→对应边的比相等→△ABD∽△ACE.【自主解答】(1)△ABC∽△ADE,△ABD∽△ACE.
(2)①证△ABC∽△ADE.∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.又∵∠ABC=∠ADE,
∴△ABC∽△ADE.
②证△ABD∽△ACE.
∵△ABC∽△ADE,∴
又∵∠BAD=∠CAE,∴△ABD∽△ACE.【想一想】
此题中如果已知△ABD∽△ACE,如何证明△ABC∽△ADE.
提示:∵△ABD∽△ACE,
∴∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
又∵
又∵∠BAC=∠DAE,
∴△ABC∽△ADE.【微点拨】
证明三角形相似时,需要两个条件,如果题目中出现公共角或对顶角时,需要再证明另一角相等,或者证明夹这个角的两边成比例.【方法一点通】
相似三角形的判定方法的选择
1.三边成比例:当给出的边比较多或者有边的比例关系时,选用三边成比例判定.
2.两组角相等:当出现平行线、对顶角、公共角或者给出几个角的大小时,选用两组角对应相等判定.
3.两组边对应成比例且夹角相等:当已知条件中只有一组角相等时,通过证明夹角的两边成比例判定.知识点二 相似三角形判定的综合应用
【示范题2】如图,AB=3AC,BD=3AE,又BD∥AC,点B,A,E在同一条
直线上.
(1)求证:△ABD∽△CAE.(2)如果AC=BD,AD=2 BD,设BD=a,求
BC的长.【思路点拨】
(1)证等比→证等角→得结论
(2)等量代换→求出∠D→求出∠E→求出BC
【自主解答】(1)∵AB=3AC,BD=3AE,∴
∵BD∥AC,∴∠EAC=∠DBA,∴△ABD∽△CAE.(2)连接BC,AB=3AC=3BD=3a,BD=3AE,∴AE= BD= a,
AD=2 BD=2 a,
在△ABD中,AB2=(3a)2=9a2,AD2+BD2=(2 a)2+a2=9a2,
∴AD2+BD2=AB2,∴∠D=90°,
由(1)知△ABD∽△CAE,∴∠E=∠D=90°,
在Rt△AEC中,EC2=AC2-AE2=a2-
在Rt△BEC中, 【想一想】
在示范题2(2)的条件下,连接CD,此时四边形ABDC是什么特殊的四边形?
提示:平行四边形.
∵AC∥BD,AC=BD,
∴四边形ABDC是平行四边形.【备选例题】已知四边形ABCD、四边形DCFE、四边形EFHG都是边长为1的正方形,则∠1+∠2+∠3是多少度?【解析】由题意知AC= ,CF=1,CH=2,
所以
又∠ACF=∠HCA,所以△ACF∽△HCA,
所以∠2=∠CAH,又因为∠1=∠3+∠CAH,
所以∠1+∠2+∠3=∠1+∠CAH+∠1-∠CAH=2∠1=90°.【方法一点通】
相似三角形判定的综合应用
1.在证明三角形相似时,经常要用到两种判定方法判定三角形相似,其中用一种判定方法证明三角形相似,是为另一种判定方法证明相似三角形作准备的.
2.用相似三角形的判定方法证明三角形相似时要注意几种方法综合应用.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
