2020北师版九上数学第四章图形的相似4.6、4.7相似三角形的性质习题课件(25张PPT)
文档属性
| 名称 | 2020北师版九上数学第四章图形的相似4.6、4.7相似三角形的性质习题课件(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 19:28:33 | ||
图片预览








文档简介
课件25张PPT。6
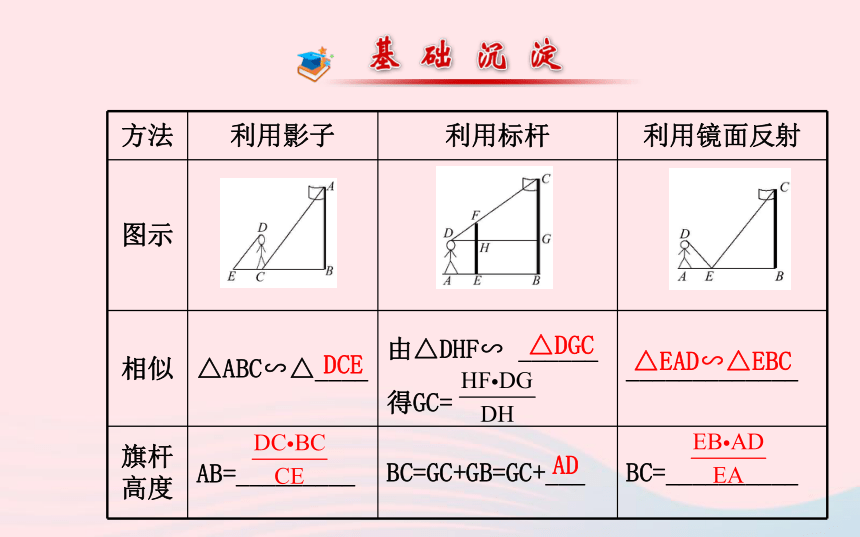
利用相似三角形测高DCE△DGC△EAD∽△EBCAD【思维诊断】(打“√”或“×”)
1.用标杆测量时,眼睛必须和标杆的顶端、被测物体顶端共
线. ( )
2.在阳光下,两个物体的长度与影长成正比. ( )
3.在灯光下,不同的物体的影长也有可能相同. ( )
4.利用镜面反射测量物体的高度时,不必遵循平面镜的反射定律. ( ) √×√×知识点 应用相似三角形测量物体的高度
【示范题】某同学想测量旗杆的高度,他在某一
时刻测得1m长的竹竿竖直时影长为1.5m.在同一
时刻测量旗杆的影长时,因旗杆靠近一幢楼房,影
子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21m,留在墙上的影子为2m,你能帮助他求出旗杆的高度吗?【思路点拨】根据太阳光下某一时刻,物高与影长成正比,只需要求出落在地面上的21m长的影长是旗杆的哪一部分形成的即可.过点C作CE∥BD,交AB于点E.【自主解答】过点C作CE∥BD,交AB于点E,得四边形BDCE是矩形,则BE=CD=2m,CE=BD=21m.
设AE=x,根据题意得
即 解得x=14,
所以旗杆的高度为14+2=16(m).【想一想】
除例题解法外,还有其他方法吗?
提示:延长BD交AC的延长线于点F,先求得DF,然后得旗杆的影长,最后根据比例式解之.【备选例题】如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.【解析】因为CD∥EF∥AB,
所以可以得到△CDF∽△ABF,△EFG∽△ABG,
所以
又因为CD=EF,所以
因为DF=3,FG=4,BF=BD+DF=BD+3,
BG=BD+DF+FG=BD+7,所以
所以BD=9m,BF=9+3=12(m),
所以 解得,AB=6.4m.【方法一点通】
利用相似三角形测量物体高度的一般步骤
1.画出示意图,利用平行光线、影子、标杆等构造相似三角形.
2.测量与表示未知量的线段相对应的边长,以及另外一组对应边的长度.
3.利用相似三角形的性质列出包括以上四个量的比例式,求出未知量.
4.检验并得到答案.7
相似三角形的性质1.相似三角形中重要线段的比:相似三角形对应高的比、对应
角平分线的比、对应中线的比都等于_______.相似比2.相似三角形的周长比和面积比:
(1)相似三角形的周长比等于_______.
(2)已知:△ABC∽△A′B′C′,△ABC与△A′B′C′的相似比
为k.
若CD,C′D′分别是AB,A′B′边上的高,则 =k,
∴S△ABC= AB·CD,S△A′B′C′= A′B′·C′D′.
∴ =__.相似三角形的面
积比等于_____________.相似比k2相似比的平方【思维诊断】(打“√”或“×”)
1.两个相似三角形的相似比为3,则它们的面积比为6.( )
2.如果把一个多边形的各边都扩大5倍,则这个多边形的面积扩
大25倍. ( )
3.△ABC与△DEF的相似比为2∶3,则△DEF与△ABC的周长之比
为4∶9. ( )
4.△ABC∽△A′B′C′,它们的相似比为2,则△A′B′C′与
△ABC的面积比为2. ( )×√××知识点一相似三角形的重要线段和角
【示范题1】一块直角三角形木板的一条
直角边AB=3m,BC=4m,工人师傅要把它加
工成一个面积最大的正方形桌面,现请甲乙两位同学设计加工方案,甲设计的方案如图1,乙设计的方案如图2.你认为哪位同学设计的方案较好?试说明理由.【思路点拨】分别表示出两种图形中正方形的面积,先求出两种情况下正方形的边长,然后求出面积比较大小.【自主解答】按图1设计,设正方形的边长为x,
因为DE∥AB,所以∠CDE=∠CBA,∠CED=∠CAB,
所以△CDE∽△CBA,所以
按图2设计,如图所示,过点B作斜边AC边上的高BH,垂足为H,交DE于P,因为AB·BC=AC·BH,解得BH=2.4,设正方形的边长为y,
因为DE∥AC,所以∠BDE=∠A,∠BED=∠C,
所以△BDE∽△BAC,所以
即 因为x>y,所以x2>y2,
所以甲同学设计的方案较好.【想一想】
在本例中,求解两种方案中正方形的边长时,都运用了什么知识?
提示:都运用了相似三角形的性质.【微点拨】运用相似三角形对应边上高的比的两点注意
1.图形:相似三角形对应边上高的比常见图形
如下,即三角形中存在一个矩形.
2.方法:习惯上,利用相似三角形对应边上高的
比等于相似比列方程求解.【方法一点通】
相似三角形性质的“四种作用”
(1)求解线段的长度和角的度数.
(2)计算三角形的周长及面积.
(3)证明线段的比例关系、角相等.
(4)计算线段的比及线段的平方比.知识点二 相似三角形的周长与面积
【示范题2】如图,梯形
ABCD中,AD∥BC,对角线AC,BD相交于O,AD=1,
BC=4,则△AOD与△BOC的面积比等于( )
【教你解题】【想一想】
示范题2中△AOB和△DOC有什么关系?
提示:△AOB和△DOC面积相等.【方法一点通】
相似图形的周长与面积的计算
1.常见图形结构:“A”型图与“X”型图,应用平行线构造相似三角形,常与平行四边形联系在一起.
2.解题关键:一是准确把握相似三角形的周长的比与面积的比和相似比的关系;二是掌握同底等高或等底同高的三角形面积之间的相等关系.
利用相似三角形测高DCE△DGC△EAD∽△EBCAD【思维诊断】(打“√”或“×”)
1.用标杆测量时,眼睛必须和标杆的顶端、被测物体顶端共
线. ( )
2.在阳光下,两个物体的长度与影长成正比. ( )
3.在灯光下,不同的物体的影长也有可能相同. ( )
4.利用镜面反射测量物体的高度时,不必遵循平面镜的反射定律. ( ) √×√×知识点 应用相似三角形测量物体的高度
【示范题】某同学想测量旗杆的高度,他在某一
时刻测得1m长的竹竿竖直时影长为1.5m.在同一
时刻测量旗杆的影长时,因旗杆靠近一幢楼房,影
子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21m,留在墙上的影子为2m,你能帮助他求出旗杆的高度吗?【思路点拨】根据太阳光下某一时刻,物高与影长成正比,只需要求出落在地面上的21m长的影长是旗杆的哪一部分形成的即可.过点C作CE∥BD,交AB于点E.【自主解答】过点C作CE∥BD,交AB于点E,得四边形BDCE是矩形,则BE=CD=2m,CE=BD=21m.
设AE=x,根据题意得
即 解得x=14,
所以旗杆的高度为14+2=16(m).【想一想】
除例题解法外,还有其他方法吗?
提示:延长BD交AC的延长线于点F,先求得DF,然后得旗杆的影长,最后根据比例式解之.【备选例题】如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.【解析】因为CD∥EF∥AB,
所以可以得到△CDF∽△ABF,△EFG∽△ABG,
所以
又因为CD=EF,所以
因为DF=3,FG=4,BF=BD+DF=BD+3,
BG=BD+DF+FG=BD+7,所以
所以BD=9m,BF=9+3=12(m),
所以 解得,AB=6.4m.【方法一点通】
利用相似三角形测量物体高度的一般步骤
1.画出示意图,利用平行光线、影子、标杆等构造相似三角形.
2.测量与表示未知量的线段相对应的边长,以及另外一组对应边的长度.
3.利用相似三角形的性质列出包括以上四个量的比例式,求出未知量.
4.检验并得到答案.7
相似三角形的性质1.相似三角形中重要线段的比:相似三角形对应高的比、对应
角平分线的比、对应中线的比都等于_______.相似比2.相似三角形的周长比和面积比:
(1)相似三角形的周长比等于_______.
(2)已知:△ABC∽△A′B′C′,△ABC与△A′B′C′的相似比
为k.
若CD,C′D′分别是AB,A′B′边上的高,则 =k,
∴S△ABC= AB·CD,S△A′B′C′= A′B′·C′D′.
∴ =__.相似三角形的面
积比等于_____________.相似比k2相似比的平方【思维诊断】(打“√”或“×”)
1.两个相似三角形的相似比为3,则它们的面积比为6.( )
2.如果把一个多边形的各边都扩大5倍,则这个多边形的面积扩
大25倍. ( )
3.△ABC与△DEF的相似比为2∶3,则△DEF与△ABC的周长之比
为4∶9. ( )
4.△ABC∽△A′B′C′,它们的相似比为2,则△A′B′C′与
△ABC的面积比为2. ( )×√××知识点一相似三角形的重要线段和角
【示范题1】一块直角三角形木板的一条
直角边AB=3m,BC=4m,工人师傅要把它加
工成一个面积最大的正方形桌面,现请甲乙两位同学设计加工方案,甲设计的方案如图1,乙设计的方案如图2.你认为哪位同学设计的方案较好?试说明理由.【思路点拨】分别表示出两种图形中正方形的面积,先求出两种情况下正方形的边长,然后求出面积比较大小.【自主解答】按图1设计,设正方形的边长为x,
因为DE∥AB,所以∠CDE=∠CBA,∠CED=∠CAB,
所以△CDE∽△CBA,所以
按图2设计,如图所示,过点B作斜边AC边上的高BH,垂足为H,交DE于P,因为AB·BC=AC·BH,解得BH=2.4,设正方形的边长为y,
因为DE∥AC,所以∠BDE=∠A,∠BED=∠C,
所以△BDE∽△BAC,所以
即 因为x>y,所以x2>y2,
所以甲同学设计的方案较好.【想一想】
在本例中,求解两种方案中正方形的边长时,都运用了什么知识?
提示:都运用了相似三角形的性质.【微点拨】运用相似三角形对应边上高的比的两点注意
1.图形:相似三角形对应边上高的比常见图形
如下,即三角形中存在一个矩形.
2.方法:习惯上,利用相似三角形对应边上高的
比等于相似比列方程求解.【方法一点通】
相似三角形性质的“四种作用”
(1)求解线段的长度和角的度数.
(2)计算三角形的周长及面积.
(3)证明线段的比例关系、角相等.
(4)计算线段的比及线段的平方比.知识点二 相似三角形的周长与面积
【示范题2】如图,梯形
ABCD中,AD∥BC,对角线AC,BD相交于O,AD=1,
BC=4,则△AOD与△BOC的面积比等于( )
【教你解题】【想一想】
示范题2中△AOB和△DOC有什么关系?
提示:△AOB和△DOC面积相等.【方法一点通】
相似图形的周长与面积的计算
1.常见图形结构:“A”型图与“X”型图,应用平行线构造相似三角形,常与平行四边形联系在一起.
2.解题关键:一是准确把握相似三角形的周长的比与面积的比和相似比的关系;二是掌握同底等高或等底同高的三角形面积之间的相等关系.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
