2020北师版九上数学第五章投影与视图阶段复习习题课件(29张PPT)
文档属性
| 名称 | 2020北师版九上数学第五章投影与视图阶段复习习题课件(29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 19:50:21 | ||
图片预览

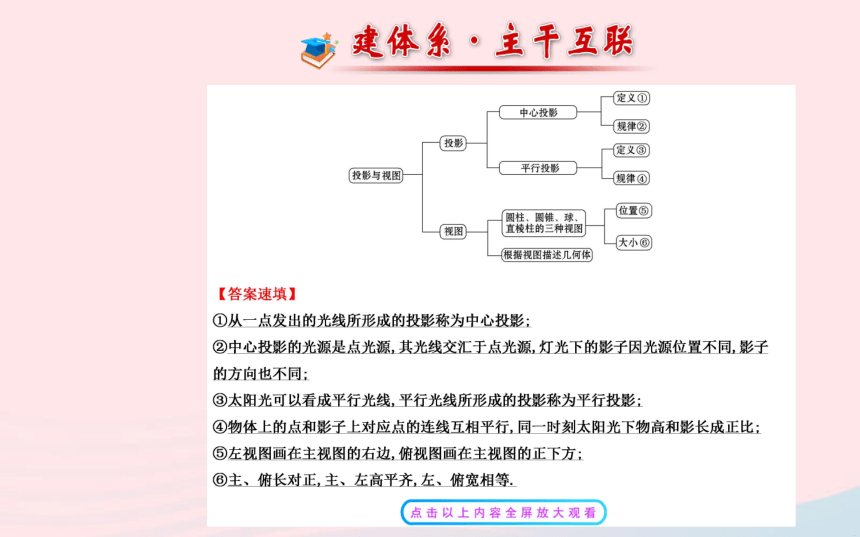




文档简介
课件29张PPT。阶段复习课
第 五 章主题1 投影及其应用
【主题训练1】一天晚上,
李明和张龙利用灯光下的影子长来测量一路
灯D的高度.如图,当李明走到点A处时,张龙测
得李明直立时身高AM与其影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处时,李明直立身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m)【自主解答】设CD长为xm,
∵AM⊥EC,CD⊥EC,BN⊥EC,EA=MA,
∴AM∥CD,BN∥CD,∴EC=CD=x,△ABN∽△ACD,
∴ 解得x=6.125≈6.1,
∴路灯的高CD的长约为6.1m.【主题升华】
1.分类:(1)平行投影:由平行光线形成的投影.
(2)中心投影:由点光源发出的光线形成的投影.
2.性质:
(1)平行投影:同一时刻,垂直于投影面的物体,物高与影长成比例.
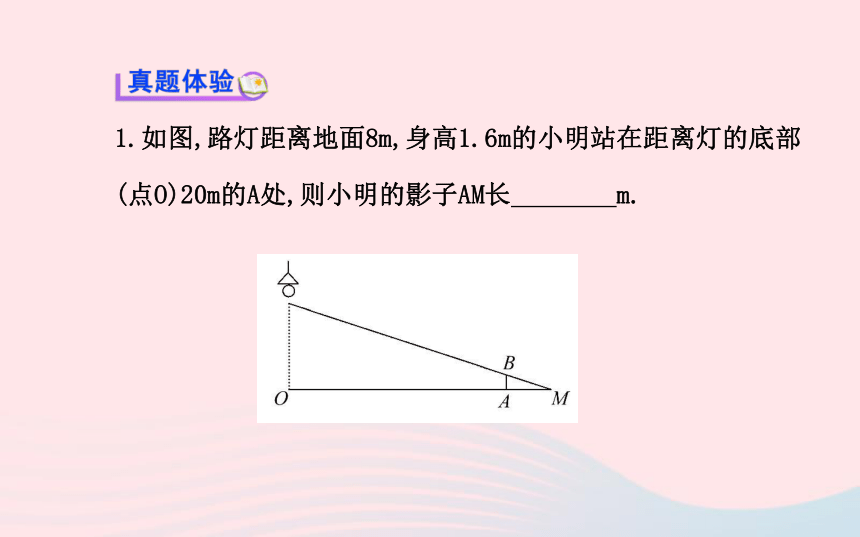
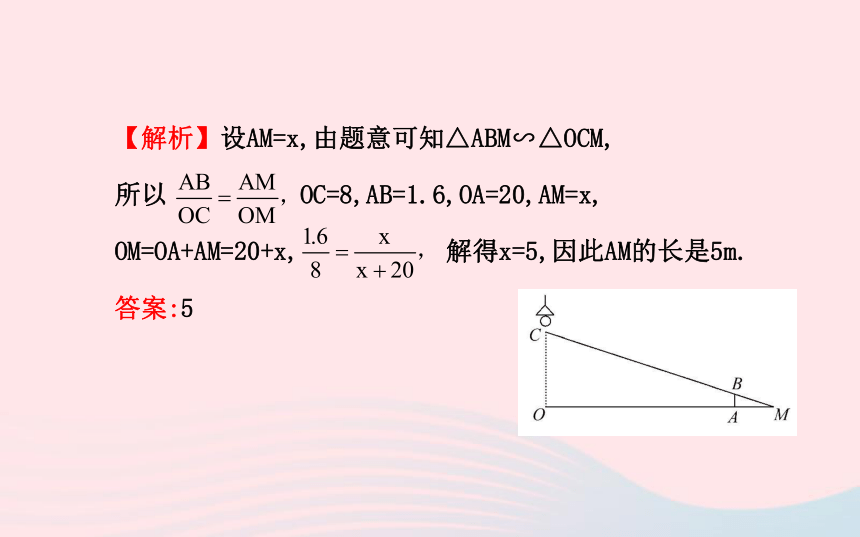
(2)中心投影:物体平行于投影面时,原物体与投影关于点光源位似.1.如图,路灯距离地面8m,身高1.6m的小明站在距离灯的底部(点O)20m的A处,则小明的影子AM长 m.【解析】设AM=x,由题意可知△ABM∽△OCM,
所以 OC=8,AB=1.6,OA=20,AM=x,
OM=OA+AM=20+x, 解得x=5,因此AM的长是5m.
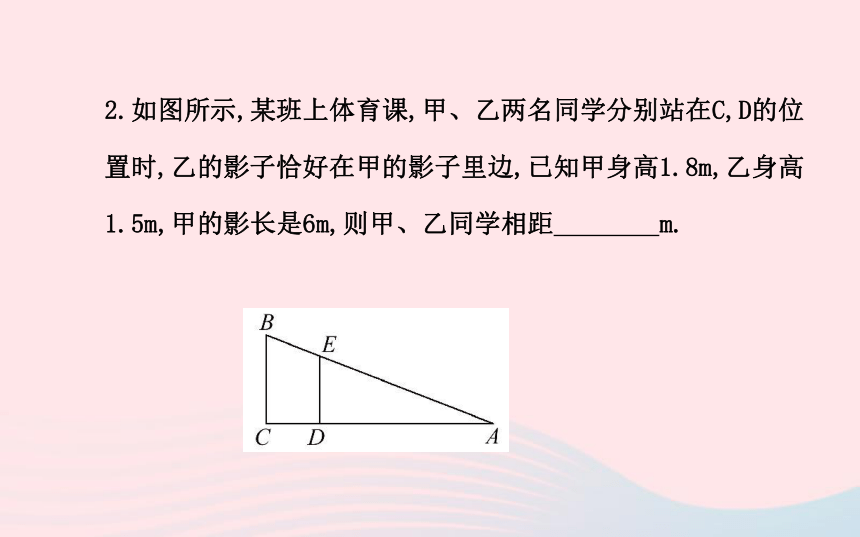
答案:52.如图所示,某班上体育课,甲、乙两名同学分别站在C,D的位置时,乙的影子恰好在甲的影子里边,已知甲身高1.8m,乙身高1.5m,甲的影长是6m,则甲、乙同学相距 m.【解析】由题意得,△ADE∽△ACB,所以 AC=6m,BC=1.8m,DE=1.5m,所以AD=5m,所以CD=6-5=1(m).
答案:1【知识归纳】
1.平行投影的有关计算问题大都与三角形及三角形相似联系在一起,在解答时要注意投影与三角形相似等性质的综合应用.
2.在平行投影下,无论物体与投影面的位置关系怎样及光线与投影面的位置关系如何,都不改变物体中线的平行关系.3.如图是住宅区内的两幢
楼,它们的高AB=CD=30m,两楼间的距离AC=30m,
现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m, =1.73).
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?【解析】(1)如图,延长QB交DC于E,作EF⊥AB,交AB于F,
在Rt△BEF中,∵EF=AC=30m,∠FEB=30°,
∴BE=2BF.设BF=xm,则BE=2xm.
根据勾股定理知BE2=BF2+EF2,
∴(2x)2=x2+302,∴x=10 (负值舍去),∴x≈17.3.
因此,EC=30-17.3=12.7(m).(2)当甲幢楼的影子刚好落在点C处时,△ABC为等腰直角三角形,因此,当太阳光与水平线夹角为45°时,甲楼的影子刚好不落在乙楼的墙上.4.两棵树的高度分别为AB=6m,CD=8m,两树的根部间的距离AC=4m,小强正在距树AB20m的点P处从左向右前进,如果小强的眼睛与地面距离为1.6m,当小强前进多少米时,就恰好不能看到CD的树顶D?【解析】设FG=xm,那么FH=x+GH=x+AC=x+4(m).
∵AB=6m,CD=8m,小强的眼睛与地面的距离为1.6m,
∴BG=4.4m,DH=6.4m,
∵BA⊥PC,CD⊥PC,∴AB∥CD,
∴FG∶FH=BG∶DH,即FG·DH=FH·BG,
∴6.4x=4.4(x+4),∴x=8.8,
20-8.8=11.2(m).
答:前进11.2m时恰好不能看到CD的树顶D.主题2 几何体的三种视图
【主题训练2】如图,由三个小立方块搭成的俯视图是 ( )【自主解答】选A.从上面观察这个几何体,得到的平面图形是左边一个正方形,右边一个正方形,且大小相同.因此,符合题意的俯视图是A.【备选例题】由一些大小相同的小正方体搭成的几何体的左视图和俯视图,如图所示,则搭成该几何体的小正方体的个数最少是 ( )
A.4 B.5 C.6 D.7【解析】选C.根据左视图和俯视图可知该几何体每个位置小正方体的个数可能有以下三种情形(小正方体个数相同的只提供一种),其中小正方体的个数最少是6个.【主题升华】
1.三视图与投影的关系:三视图是平行光线垂直于投影面时的投影,即正投影.
2.三视图之间的关系:
(1)长对正:主视图与俯视图的长相等.
(2)高平齐:主视图与左视图的高相等.
(3)宽相等:左视图与俯视图的宽相等.1.如图是由6个大小相同的正方体组成的几何体,它的左视图是 ( )
【解析】选A.从左边看,左边一列有两个正方体,右边有一个,故选A.2.图中所示的几何体为圆台,其主视图正确的是 ( )
【解析】选A.根据主视图的概念,该物体的主视图是选项A中的平面图形.3.一个立体图形的三种视图如图所示,根据图中数据求得这个立体图形的表面积为 ( )
A.2π B.6π C.7π D.8π【解析】选D.根据三种视图知该几何体为圆柱,圆柱的侧面积为:2π×3=6π,底面积为:π× =π,所以圆柱的表面积为:6π+2π=8π.4.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多有( )
A.4 B.5 C.6 D.7【解析】选C.由俯视图可知,该几何体有两行两列,再由主视图可知第一层有4个小立方块;第2层的左边一列最多有2个小立方块,所以组成这个几何体的小正方体的个数最多是4+2=6.5.并排放置的等底等高的圆锥和圆柱(如图)的主视图是( )【解析】选B.A的两个图是图中两个几何体的俯视图,不是主视图;C是左视图,D是从右侧观察的结果,但图中缺少虚线,故都不正确,只有B正确.6.有一篮球如图放置,其主视图为 ( )
【解析】选B.从篮球的前方“正对着”观察得到的形状是圆,故选B.
第 五 章主题1 投影及其应用
【主题训练1】一天晚上,
李明和张龙利用灯光下的影子长来测量一路
灯D的高度.如图,当李明走到点A处时,张龙测
得李明直立时身高AM与其影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处时,李明直立身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m)【自主解答】设CD长为xm,
∵AM⊥EC,CD⊥EC,BN⊥EC,EA=MA,
∴AM∥CD,BN∥CD,∴EC=CD=x,△ABN∽△ACD,
∴ 解得x=6.125≈6.1,
∴路灯的高CD的长约为6.1m.【主题升华】
1.分类:(1)平行投影:由平行光线形成的投影.
(2)中心投影:由点光源发出的光线形成的投影.
2.性质:
(1)平行投影:同一时刻,垂直于投影面的物体,物高与影长成比例.
(2)中心投影:物体平行于投影面时,原物体与投影关于点光源位似.1.如图,路灯距离地面8m,身高1.6m的小明站在距离灯的底部(点O)20m的A处,则小明的影子AM长 m.【解析】设AM=x,由题意可知△ABM∽△OCM,
所以 OC=8,AB=1.6,OA=20,AM=x,
OM=OA+AM=20+x, 解得x=5,因此AM的长是5m.
答案:52.如图所示,某班上体育课,甲、乙两名同学分别站在C,D的位置时,乙的影子恰好在甲的影子里边,已知甲身高1.8m,乙身高1.5m,甲的影长是6m,则甲、乙同学相距 m.【解析】由题意得,△ADE∽△ACB,所以 AC=6m,BC=1.8m,DE=1.5m,所以AD=5m,所以CD=6-5=1(m).
答案:1【知识归纳】
1.平行投影的有关计算问题大都与三角形及三角形相似联系在一起,在解答时要注意投影与三角形相似等性质的综合应用.
2.在平行投影下,无论物体与投影面的位置关系怎样及光线与投影面的位置关系如何,都不改变物体中线的平行关系.3.如图是住宅区内的两幢
楼,它们的高AB=CD=30m,两楼间的距离AC=30m,
现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m, =1.73).
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?【解析】(1)如图,延长QB交DC于E,作EF⊥AB,交AB于F,
在Rt△BEF中,∵EF=AC=30m,∠FEB=30°,
∴BE=2BF.设BF=xm,则BE=2xm.
根据勾股定理知BE2=BF2+EF2,
∴(2x)2=x2+302,∴x=10 (负值舍去),∴x≈17.3.
因此,EC=30-17.3=12.7(m).(2)当甲幢楼的影子刚好落在点C处时,△ABC为等腰直角三角形,因此,当太阳光与水平线夹角为45°时,甲楼的影子刚好不落在乙楼的墙上.4.两棵树的高度分别为AB=6m,CD=8m,两树的根部间的距离AC=4m,小强正在距树AB20m的点P处从左向右前进,如果小强的眼睛与地面距离为1.6m,当小强前进多少米时,就恰好不能看到CD的树顶D?【解析】设FG=xm,那么FH=x+GH=x+AC=x+4(m).
∵AB=6m,CD=8m,小强的眼睛与地面的距离为1.6m,
∴BG=4.4m,DH=6.4m,
∵BA⊥PC,CD⊥PC,∴AB∥CD,
∴FG∶FH=BG∶DH,即FG·DH=FH·BG,
∴6.4x=4.4(x+4),∴x=8.8,
20-8.8=11.2(m).
答:前进11.2m时恰好不能看到CD的树顶D.主题2 几何体的三种视图
【主题训练2】如图,由三个小立方块搭成的俯视图是 ( )【自主解答】选A.从上面观察这个几何体,得到的平面图形是左边一个正方形,右边一个正方形,且大小相同.因此,符合题意的俯视图是A.【备选例题】由一些大小相同的小正方体搭成的几何体的左视图和俯视图,如图所示,则搭成该几何体的小正方体的个数最少是 ( )
A.4 B.5 C.6 D.7【解析】选C.根据左视图和俯视图可知该几何体每个位置小正方体的个数可能有以下三种情形(小正方体个数相同的只提供一种),其中小正方体的个数最少是6个.【主题升华】
1.三视图与投影的关系:三视图是平行光线垂直于投影面时的投影,即正投影.
2.三视图之间的关系:
(1)长对正:主视图与俯视图的长相等.
(2)高平齐:主视图与左视图的高相等.
(3)宽相等:左视图与俯视图的宽相等.1.如图是由6个大小相同的正方体组成的几何体,它的左视图是 ( )
【解析】选A.从左边看,左边一列有两个正方体,右边有一个,故选A.2.图中所示的几何体为圆台,其主视图正确的是 ( )
【解析】选A.根据主视图的概念,该物体的主视图是选项A中的平面图形.3.一个立体图形的三种视图如图所示,根据图中数据求得这个立体图形的表面积为 ( )
A.2π B.6π C.7π D.8π【解析】选D.根据三种视图知该几何体为圆柱,圆柱的侧面积为:2π×3=6π,底面积为:π× =π,所以圆柱的表面积为:6π+2π=8π.4.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多有( )
A.4 B.5 C.6 D.7【解析】选C.由俯视图可知,该几何体有两行两列,再由主视图可知第一层有4个小立方块;第2层的左边一列最多有2个小立方块,所以组成这个几何体的小正方体的个数最多是4+2=6.5.并排放置的等底等高的圆锥和圆柱(如图)的主视图是( )【解析】选B.A的两个图是图中两个几何体的俯视图,不是主视图;C是左视图,D是从右侧观察的结果,但图中缺少虚线,故都不正确,只有B正确.6.有一篮球如图放置,其主视图为 ( )
【解析】选B.从篮球的前方“正对着”观察得到的形状是圆,故选B.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
