2020北师版九上数学第一章特殊平行四边形1.2矩形的性质与判定习题课件(24张PPT)
文档属性
| 名称 | 2020北师版九上数学第一章特殊平行四边形1.2矩形的性质与判定习题课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 00:00:00 | ||
图片预览








文档简介
课件24张PPT。2 矩形的性质与判定
第1课时1.矩形的概念:
有一个角是_____的平行四边形叫做矩形.
2.矩形的性质:
(1)矩形具有___________的一切性质.
(2)矩形的四个角都是_____.
(3)矩形的对角线_____.
(4)矩形是轴对称图形,它有___条对称轴.直角平行四边形直角相等两3.直角三角形斜边上中线的性质:
直角三角形斜边上的中线等于斜边的_____.一半【思维诊断】(打“√”或“×”)
1.矩形是平行四边形,也是特殊的菱形. ( )
2.矩形的对角线垂直且相等. ( )
3.矩形的每条对角线平分一组对角. ( )
4.矩形是轴对称图形但不是中心对称图形. ( )××××知识点一 矩形的性质与应用
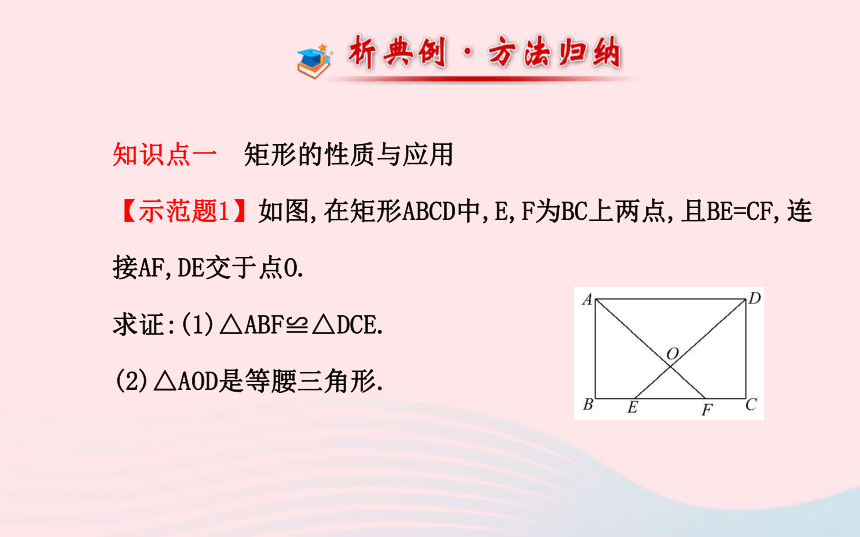
【示范题1】如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.
求证:(1)△ABF≌△DCE.
(2)△AOD是等腰三角形.【解题探究】(1)根据矩形的性质可得∠B=∠C=90°,AB=DC,还需要什么条件才能证明△ABF和△DCE全等?
提示:只要证明BF=CE,根据SAS可得△ABF≌△DCE.
(2)我们常通过“等角对等边”证明等腰三角形,本题要证明哪两个角相等才能证明△AOD是等腰三角形?
提示:利用矩形的性质、全等三角形的性质证明∠DAF=∠EDA即可.【尝试解答】(1)在矩形ABCD中,∠B=∠C=90°,AB=DC,
∵BE=CF,BF=BC-FC,CE=BC-BE,∴BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS).
(2)∵△ABF≌△DCE,∴∠BAF=∠CDE,
∵∠DAF=∠BAD-∠BAF=90°-∠BAF,
∠EDA=∠CDA-∠EDC=90°-∠EDC,
∴∠DAF=∠EDA,∴△AOD是等腰三角形.【想一想】
在第(2)问中,△EOF是等腰三角形吗?为什么?
提示:△EOF是等腰三角形,
∵△ABF≌△DCE,
∴∠OEF=∠OFE,
∴OE=OF,
即△EOF是等腰三角形.【微点拨】
1.矩形有两条对称轴,经过两组对边中点的直线都是它的对称轴.
2.矩形的两条对角线把它分成四个等腰三角形.
3.与矩形有关的问题常转化为等腰三角形或直角三角形求解.【方法一点通】
矩形性质的常见应用
(1)证明线段的平行、相等或倍分关系.
(2)证明角相等或求角的度数.
(3)解决与全等或相似有关的问题.知识点二 直角三角形斜边上中线的性质
【示范题2】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于H,连接OH.
求证:∠DHO=∠DCO.【思路点拨】OD=OB→OH=OB→∠OHB=∠OBH,∠OBH=∠ODC→
∠OHB=∠ODC→∠DHO=∠DCO.
【自主解答】∵四边形ABCD是菱形,∴OD=OB,∠COD=90°,
∵DH⊥AB,∴OH=OB,∴∠OHB=∠OBH,
又∵AB∥CD,∴∠OBH=∠ODC,∴∠OHB=∠ODC.
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,∴∠DHO=∠DCO.【想一想】
在本题中,除了∠DCO外,还有哪些角等于∠DHO?
提示:和∠DHO相等的角还有∠BCO,∠BAO,∠DAO,∠HDO.【方法一点通】
直角三角形斜边上中线的“三个应用”
1.证明线段相等或倍分关系.
2.证明角相等.
3.其逆定理可作为证明直角三角形的理论依据.2 矩形的性质与判定
第2课时矩形的判定:
(1)定义:有一个角是_____的平行四边形是矩形.
应用格式:在□ABCD中,∠A=90°,∴四边形ABCD为矩形.
(2)对角线:对角线_____的___________是矩形.
应用格式:在□ABCD中,AC=BD,∴四边形ABCD为矩形.
(3)角:有三个角是_____的四边形是矩形.
应用格式:在四边形ABCD中,∠A=∠B=∠C=90°,∴四边形ABCD为矩形.直角相等平行四边形直角【思维诊断】(打“√”或“×”)
1.有一个角是直角的四边形是矩形. ( )
2.对角线相等的四边形是矩形. ( )
3.四个角都相等的四边形是矩形. ( )××√知识点 矩形的判定与应用
【示范题】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有何数量关系,为什么?
(2)当△ABC满足什么条件时,四边形AFBD
是矩形?请说明理由.【思路点拨】(1)AF∥BC→∠AFE=∠DCE→△AEF≌△DEC→AF=CD→BD=CD.
(2)AB=AC,BD=CD→AD⊥BC→四边形AFBD是矩形.【自主解答】(1)BD=CD.理由如下:
∵AF∥BC,AF=BD,∴四边形AFBD是平行四边形.
∵AF∥BC,∴∠AFE=∠DCE,∠FAE=∠CDE,
又∵E是AD的中点,∴AE=DE.∴△AFE≌△DCE.
∴AF=CD.又∵AF=BD,∴BD=CD.
(2)当△ABC满足AB=AC时,四边形AFBD是矩形.理由如下:
∵AB=AC,BD=CD,∴AD⊥BC.∴∠ADB=90°.
又∵四边形AFBD是平行四边形,∴四边形AFBD是矩形.【想一想】
在本题中,当△ABC满足什么条件时,四边形AFBD是菱形?请说明理由.
提示:当∠BAC=90°时,四边形AFBD是菱形.理由如下:
∵∠BAC=90°,BD=CD,
∴AD=BD.
又∵四边形AFBD是平行四边形,
∴四边形AFBD是菱形.【备选例题】如图,在四边形ABCD中,∠A
=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.【证明】作BF⊥CE于F,
∵∠BCF+∠DCE=90°,∠D+∠DCE=90°,
∴∠BCF=∠D,又BC=CD,
∴Rt△BCF≌Rt△CDE,∴BF=CE,
又∠BFE=∠AEF=∠A=90°,∴四边形ABFE是矩形,
∴BF=AE,∴AE=CE.【方法一点通】
矩形常用的判定方法
第1课时1.矩形的概念:
有一个角是_____的平行四边形叫做矩形.
2.矩形的性质:
(1)矩形具有___________的一切性质.
(2)矩形的四个角都是_____.
(3)矩形的对角线_____.
(4)矩形是轴对称图形,它有___条对称轴.直角平行四边形直角相等两3.直角三角形斜边上中线的性质:
直角三角形斜边上的中线等于斜边的_____.一半【思维诊断】(打“√”或“×”)
1.矩形是平行四边形,也是特殊的菱形. ( )
2.矩形的对角线垂直且相等. ( )
3.矩形的每条对角线平分一组对角. ( )
4.矩形是轴对称图形但不是中心对称图形. ( )××××知识点一 矩形的性质与应用
【示范题1】如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.
求证:(1)△ABF≌△DCE.
(2)△AOD是等腰三角形.【解题探究】(1)根据矩形的性质可得∠B=∠C=90°,AB=DC,还需要什么条件才能证明△ABF和△DCE全等?
提示:只要证明BF=CE,根据SAS可得△ABF≌△DCE.
(2)我们常通过“等角对等边”证明等腰三角形,本题要证明哪两个角相等才能证明△AOD是等腰三角形?
提示:利用矩形的性质、全等三角形的性质证明∠DAF=∠EDA即可.【尝试解答】(1)在矩形ABCD中,∠B=∠C=90°,AB=DC,
∵BE=CF,BF=BC-FC,CE=BC-BE,∴BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS).
(2)∵△ABF≌△DCE,∴∠BAF=∠CDE,
∵∠DAF=∠BAD-∠BAF=90°-∠BAF,
∠EDA=∠CDA-∠EDC=90°-∠EDC,
∴∠DAF=∠EDA,∴△AOD是等腰三角形.【想一想】
在第(2)问中,△EOF是等腰三角形吗?为什么?
提示:△EOF是等腰三角形,
∵△ABF≌△DCE,
∴∠OEF=∠OFE,
∴OE=OF,
即△EOF是等腰三角形.【微点拨】
1.矩形有两条对称轴,经过两组对边中点的直线都是它的对称轴.
2.矩形的两条对角线把它分成四个等腰三角形.
3.与矩形有关的问题常转化为等腰三角形或直角三角形求解.【方法一点通】
矩形性质的常见应用
(1)证明线段的平行、相等或倍分关系.
(2)证明角相等或求角的度数.
(3)解决与全等或相似有关的问题.知识点二 直角三角形斜边上中线的性质
【示范题2】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于H,连接OH.
求证:∠DHO=∠DCO.【思路点拨】OD=OB→OH=OB→∠OHB=∠OBH,∠OBH=∠ODC→
∠OHB=∠ODC→∠DHO=∠DCO.
【自主解答】∵四边形ABCD是菱形,∴OD=OB,∠COD=90°,
∵DH⊥AB,∴OH=OB,∴∠OHB=∠OBH,
又∵AB∥CD,∴∠OBH=∠ODC,∴∠OHB=∠ODC.
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,∴∠DHO=∠DCO.【想一想】
在本题中,除了∠DCO外,还有哪些角等于∠DHO?
提示:和∠DHO相等的角还有∠BCO,∠BAO,∠DAO,∠HDO.【方法一点通】
直角三角形斜边上中线的“三个应用”
1.证明线段相等或倍分关系.
2.证明角相等.
3.其逆定理可作为证明直角三角形的理论依据.2 矩形的性质与判定
第2课时矩形的判定:
(1)定义:有一个角是_____的平行四边形是矩形.
应用格式:在□ABCD中,∠A=90°,∴四边形ABCD为矩形.
(2)对角线:对角线_____的___________是矩形.
应用格式:在□ABCD中,AC=BD,∴四边形ABCD为矩形.
(3)角:有三个角是_____的四边形是矩形.
应用格式:在四边形ABCD中,∠A=∠B=∠C=90°,∴四边形ABCD为矩形.直角相等平行四边形直角【思维诊断】(打“√”或“×”)
1.有一个角是直角的四边形是矩形. ( )
2.对角线相等的四边形是矩形. ( )
3.四个角都相等的四边形是矩形. ( )××√知识点 矩形的判定与应用
【示范题】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有何数量关系,为什么?
(2)当△ABC满足什么条件时,四边形AFBD
是矩形?请说明理由.【思路点拨】(1)AF∥BC→∠AFE=∠DCE→△AEF≌△DEC→AF=CD→BD=CD.
(2)AB=AC,BD=CD→AD⊥BC→四边形AFBD是矩形.【自主解答】(1)BD=CD.理由如下:
∵AF∥BC,AF=BD,∴四边形AFBD是平行四边形.
∵AF∥BC,∴∠AFE=∠DCE,∠FAE=∠CDE,
又∵E是AD的中点,∴AE=DE.∴△AFE≌△DCE.
∴AF=CD.又∵AF=BD,∴BD=CD.
(2)当△ABC满足AB=AC时,四边形AFBD是矩形.理由如下:
∵AB=AC,BD=CD,∴AD⊥BC.∴∠ADB=90°.
又∵四边形AFBD是平行四边形,∴四边形AFBD是矩形.【想一想】
在本题中,当△ABC满足什么条件时,四边形AFBD是菱形?请说明理由.
提示:当∠BAC=90°时,四边形AFBD是菱形.理由如下:
∵∠BAC=90°,BD=CD,
∴AD=BD.
又∵四边形AFBD是平行四边形,
∴四边形AFBD是菱形.【备选例题】如图,在四边形ABCD中,∠A
=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.【证明】作BF⊥CE于F,
∵∠BCF+∠DCE=90°,∠D+∠DCE=90°,
∴∠BCF=∠D,又BC=CD,
∴Rt△BCF≌Rt△CDE,∴BF=CE,
又∠BFE=∠AEF=∠A=90°,∴四边形ABFE是矩形,
∴BF=AE,∴AE=CE.【方法一点通】
矩形常用的判定方法
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
