人教A版高中数学 选修2-2 第一章 1.5.3定积分的概念 课件(共39张PPT)
文档属性
| 名称 | 人教A版高中数学 选修2-2 第一章 1.5.3定积分的概念 课件(共39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 10:57:04 | ||
图片预览











文档简介
(共39张PPT)
1.5 定积分的概念
从求曲边梯形面积以及求变速直线运动路程可以发现,它们都是通过“四步曲”:分割、近似代替、求和、取极限得到解决,且都可以归结为求一个特定形式和的极限.都采用了在局部小范围内“以直代曲”“以不变代变”和“逼近”的思想.
新课导入
“无限细分,无限求和”的积分思想在古代就已经萌芽.最早可以追溯到希腊由阿基米德(Archimedes ,287 BC~212 BC)等人提出的计算面积和体积的方法.
这节我们学习定积分的概念.
1.5.3 定积分的概念
解决曲边梯形面积和变速直线运动的共同特征:
都通过“四步曲”——分割、近似代替、求和的极限、取极限来解决问题.
最终的结果都归结为求同一种类型的和式.
教学目标
知识与能力
理解定积分的概念、性质以及其在生活实践中的应用.
过程与方法
在研究曲边梯形面积和变速直线运动路程的基础上,通过概括它们的共同特征而引入定积分概念,给出定积分的几何意义与基本性质.
情感态度与价值观
了解解决曲边梯形面积和变速直线运动的共同特征,引出定积分概念.给出定积分定义,加深学生对定积分概念的理解.
教学重难点
重点
定积分的概念、几何定义.
难点
定积分的概念.
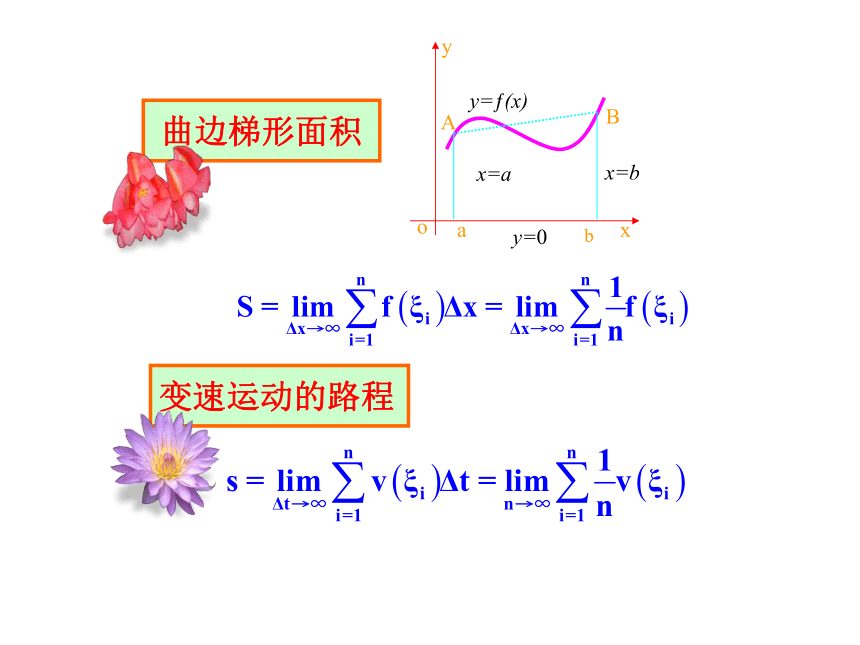
曲边梯形面积
变速运动的路程
o
x
y
y=0
y=?(x)
x=a
x=b
a
b
B
A
设函数f (x)在区间[a,b]上有界.在区间[a,b]内任意插入n-1个分点,
把区间[a,b]分成n个小区间
各个小区间的长度依次为
定积分的概念
在每个小区间
上任取一点
作和式:
被积函数
被积表达式
积分变量
积分上限
积分下限
积分和
为积分符号,函数f(x)称为被积函数,f(x)dx称为被积表达式,x称为积分变量,a称为积分下限, b称为积分上限,区间[a,b]称为积分区间.
(2)若 ,则
定积分的几何意义
(1)若 ,则
?
?
?
?
?
?
由此可知,若函数f (x)在对称区间[-a ,a]上连续,则
为偶数个时,
为奇数个时.
(3)若f(x)有正有负, 则
a
b
几何意义:
它是由曲线y=f(x)直线x=a,x=b(a 总之:定积分 在各种实际问题中所代表的实际意义不同,但它的数值在几何上都可用曲边梯形面积的代数和来表示,这就是定积分的几何意义.
定积分的性质
性质1可推广到有限个函数的情形.
即被积函数的常数因子可以提到积分号外.
(1) 性质1
(2) 性质2
(k为常数)
结论:函数的代数和的定积分等于它们的定积分的代数和.
证明:
性质1证明
结论:常数因子乘以函数的定积分,常数因子可以提到积分的符号外面来.
证明:
性质2证明
对定积分的补充规定:
(3) 性质3
(1)当a=b时,
(2)当a>b时,
如果f(x)分别在[a,b],[a,c],[c,b]上可积,那么f(x)在[a,b]上的定积分等于f(x)在[a,c][c,b]上的定积分的和.
性质3证明
我们用定积分的几何意义加以说明:
当a 总之,不论c点在[a,b]内还是[a,b]外,只要上述两个积分存在,那么,性质3总是正确的.
你想到了吗?
(4) 性质4
如果在区间[a,b]上 ,则
根据极限的性质,必有
(5) 性质5
设a 只需令F(x)=f(x)-g(x),利用性质4及性质2可得证.
(6) 性质6
(7) 性质7
(定积分中值定理)
设f(x)在区间[a,b]上连续,则在区间[a,b]上,至少存在一点 使得
证明:由闭区间上连续函数的最大值和最小值定理,存在数M和m,使m≤f(x) ≤M,a ≤x ≤b,根据性质5,有 即
或
可见数 介于 m 和M 之间,根据闭区间上连续函数的介值定理,在闭区间〔a ,b〕上至少存在一点 ,使 ,即 或
为曲边的曲边梯形面积,等于以 为高, 为底的矩形的面积.
定积分中值定理,由定积分的几何意义去理解更直观,以连续曲线
广义积分
常义积分满足:
积分区间[a,b]为有限的闭区间;
被积函数f(x)在[a,b]上有界.
广义积分: 无穷限积分;
无界函数的积分.
课堂小结
概念总结:定积分 是一种特定形式的和式 的极限,即 表示当 时,和式 所趋向的定值.
定积分
课堂练习
1、
证一证
设M及m分别是函数f(x)在区间[a,b]上的最大值及最小值则
利用定义计算
2、
3、练习
计算:
计算:
课堂答案
证明:
(此性质可用于估计积分值的大致范围)
1、
解:
①将[0,1]n等分,
②
③求和
④
即
2、
解: 由几何意义
解:如图
3、
1.5 定积分的概念
从求曲边梯形面积以及求变速直线运动路程可以发现,它们都是通过“四步曲”:分割、近似代替、求和、取极限得到解决,且都可以归结为求一个特定形式和的极限.都采用了在局部小范围内“以直代曲”“以不变代变”和“逼近”的思想.
新课导入
“无限细分,无限求和”的积分思想在古代就已经萌芽.最早可以追溯到希腊由阿基米德(Archimedes ,287 BC~212 BC)等人提出的计算面积和体积的方法.
这节我们学习定积分的概念.
1.5.3 定积分的概念
解决曲边梯形面积和变速直线运动的共同特征:
都通过“四步曲”——分割、近似代替、求和的极限、取极限来解决问题.
最终的结果都归结为求同一种类型的和式.
教学目标
知识与能力
理解定积分的概念、性质以及其在生活实践中的应用.
过程与方法
在研究曲边梯形面积和变速直线运动路程的基础上,通过概括它们的共同特征而引入定积分概念,给出定积分的几何意义与基本性质.
情感态度与价值观
了解解决曲边梯形面积和变速直线运动的共同特征,引出定积分概念.给出定积分定义,加深学生对定积分概念的理解.
教学重难点
重点
定积分的概念、几何定义.
难点
定积分的概念.
曲边梯形面积
变速运动的路程
o
x
y
y=0
y=?(x)
x=a
x=b
a
b
B
A
设函数f (x)在区间[a,b]上有界.在区间[a,b]内任意插入n-1个分点,
把区间[a,b]分成n个小区间
各个小区间的长度依次为
定积分的概念
在每个小区间
上任取一点
作和式:
被积函数
被积表达式
积分变量
积分上限
积分下限
积分和
为积分符号,函数f(x)称为被积函数,f(x)dx称为被积表达式,x称为积分变量,a称为积分下限, b称为积分上限,区间[a,b]称为积分区间.
(2)若 ,则
定积分的几何意义
(1)若 ,则
?
?
?
?
?
?
由此可知,若函数f (x)在对称区间[-a ,a]上连续,则
为偶数个时,
为奇数个时.
(3)若f(x)有正有负, 则
a
b
几何意义:
它是由曲线y=f(x)直线x=a,x=b(a
定积分的性质
性质1可推广到有限个函数的情形.
即被积函数的常数因子可以提到积分号外.
(1) 性质1
(2) 性质2
(k为常数)
结论:函数的代数和的定积分等于它们的定积分的代数和.
证明:
性质1证明
结论:常数因子乘以函数的定积分,常数因子可以提到积分的符号外面来.
证明:
性质2证明
对定积分的补充规定:
(3) 性质3
(1)当a=b时,
(2)当a>b时,
如果f(x)分别在[a,b],[a,c],[c,b]上可积,那么f(x)在[a,b]上的定积分等于f(x)在[a,c][c,b]上的定积分的和.
性质3证明
我们用定积分的几何意义加以说明:
当a
你想到了吗?
(4) 性质4
如果在区间[a,b]上 ,则
根据极限的性质,必有
(5) 性质5
设a
(6) 性质6
(7) 性质7
(定积分中值定理)
设f(x)在区间[a,b]上连续,则在区间[a,b]上,至少存在一点 使得
证明:由闭区间上连续函数的最大值和最小值定理,存在数M和m,使m≤f(x) ≤M,a ≤x ≤b,根据性质5,有 即
或
可见数 介于 m 和M 之间,根据闭区间上连续函数的介值定理,在闭区间〔a ,b〕上至少存在一点 ,使 ,即 或
为曲边的曲边梯形面积,等于以 为高, 为底的矩形的面积.
定积分中值定理,由定积分的几何意义去理解更直观,以连续曲线
广义积分
常义积分满足:
积分区间[a,b]为有限的闭区间;
被积函数f(x)在[a,b]上有界.
广义积分: 无穷限积分;
无界函数的积分.
课堂小结
概念总结:定积分 是一种特定形式的和式 的极限,即 表示当 时,和式 所趋向的定值.
定积分
课堂练习
1、
证一证
设M及m分别是函数f(x)在区间[a,b]上的最大值及最小值则
利用定义计算
2、
3、练习
计算:
计算:
课堂答案
证明:
(此性质可用于估计积分值的大致范围)
1、
解:
①将[0,1]n等分,
②
③求和
④
即
2、
解: 由几何意义
解:如图
3、
