2020湘教版八下数学第1章直角三角形阶段专题复习课件(57张)
文档属性
| 名称 | 2020湘教版八下数学第1章直角三角形阶段专题复习课件(57张) |  | |
| 格式 | zip | ||
| 文件大小 | 790.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 10:47:09 | ||
图片预览









文档简介
课件57张PPT。阶段专题复习
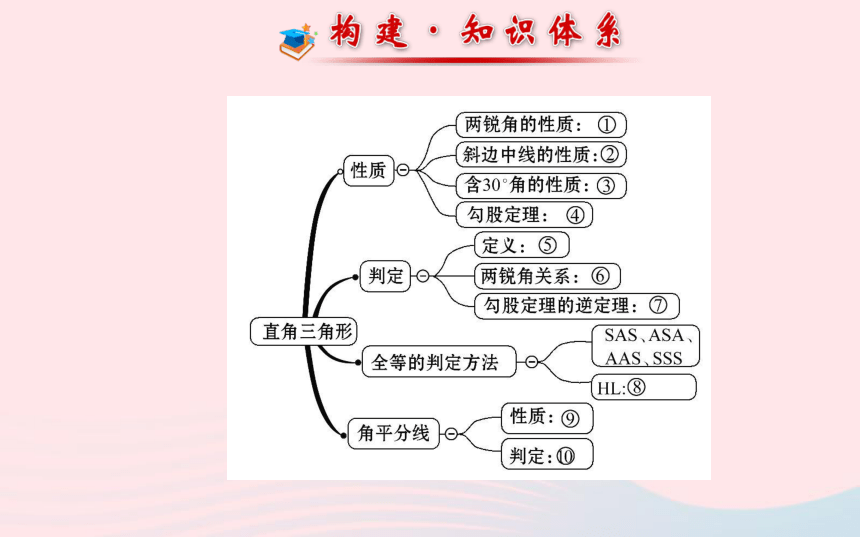
第 1 章请写出框图中数字处的内容:
①_____________________;
②_____________________________________;
③___________________________________________________
___________________;
④_________________________________________________
________;
⑤___________________________________;直角三角形两锐角互余直角三角形斜边上的中线等于斜边的一半在直角三角形中,如果一个内角等于30°,那么它所对的直角边等于斜边的一半直角三角形两直角边a,b的平方和,等于斜边c的平方,即a2+b2=c2有一个角是直角的三角形是直角三角形⑥_________________________________;
⑦___________________________________________________
_________________;
⑧____________________________________________________
______________________________;
⑨_____________________________________;
⑩_____________________________________________.有两个角互余的三角形是直角三角形如果三角形的三边长a,b,c满足关系:a2+b2=c2,那么这个三角形是直角三角形斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”)角的平分线上的点到角的两边的距离相等角的内部到角的两边距离相等的点在角的平分线上考点 1 直角三角形判定与性质的应用
【知识点睛】
1.直角三角形的相关性质:2.直角三角形判定的选择思路:
(1)当题目中有角的度数时,用定义或有两个角互余的三角形是直角三角形来判定.
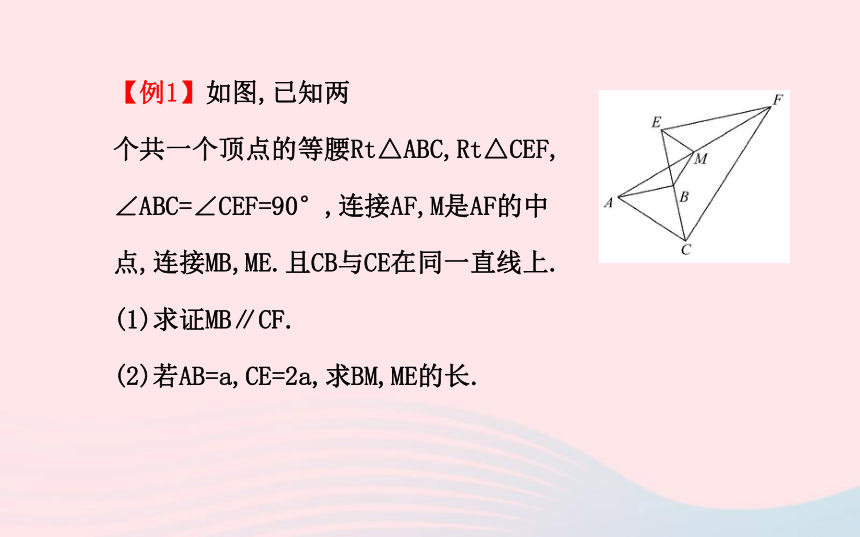
(2)当题目中有三个边的长度时,用勾股定理的逆定理判定.【例1】如图,已知两
个共一个顶点的等腰Rt△ABC,Rt△CEF,
∠ABC=∠CEF=90°,连接AF,M是AF的中
点,连接MB,ME.且CB与CE在同一直线上.
(1)求证MB∥CF.
(2)若AB=a,CE=2a,求BM,ME的长.【思路点拨】(1)连接CM,先由∠ACF=90°确定△ACF是直角三角形,可得AM=CM=FM,由SSS得△ABM≌△CBM,所以∠AMC=
2∠AMB=∠MFC+∠MCF,再由∠MFC=∠MCF得∠AMB=∠AFC,所以BM∥CF.
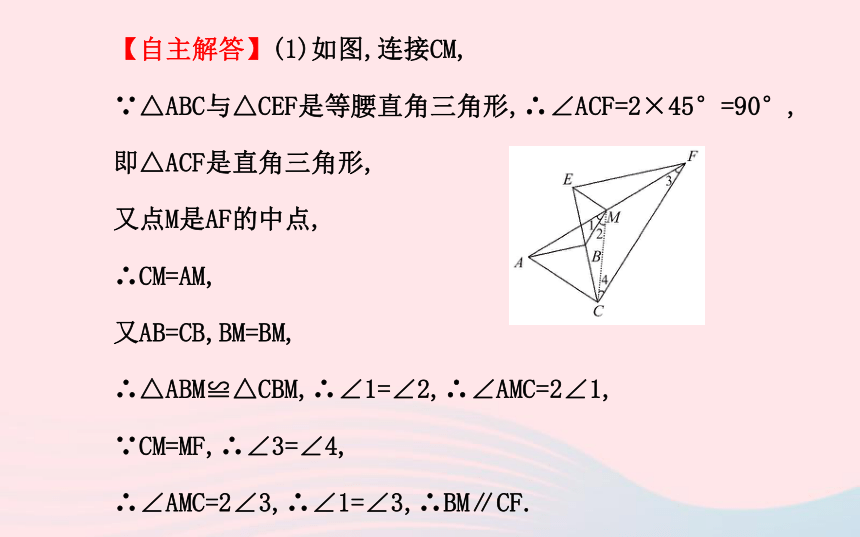
(2)由△CEM≌△FEM得出△EBM是等腰直角三角形,根据等腰直角三角形的性质求解即可.【自主解答】(1)如图,连接CM,
∵△ABC与△CEF是等腰直角三角形,∴∠ACF=2×45°=90°,
即△ACF是直角三角形,
又点M是AF的中点,
∴CM=AM,
又AB=CB,BM=BM,
∴△ABM≌△CBM,∴∠1=∠2,∴∠AMC=2∠1,
∵CM=MF,∴∠3=∠4,
∴∠AMC=2∠3,∴∠1=∠3,∴BM∥CF.(2)∵CM=FM,CE=FE,EM=EM,
∴△CEM≌△FEM,
∴∠CEM=∠FEM= ∠CEF=45°,
又由(1)可知BM∥CF,∴∠EBM=∠ECF=45°,
∴△EBM是等腰直角三角形,
∵AB=a,CE=2a,∴BE=2a-a=a,
又∵BM2+EM2=BE2,∴2BM2=2EM2=a2,
∴BM=EM= a.【中考集训】
1.如图,AB∥CD,
∠CED=90°,∠AEC=35°,则∠D的
大小为 ( )
A.65° B.55° C.45° D.35°
【解析】选B.∵AB∥CD,∴∠C=∠AEC=35°,
∵∠CED=90°,
∴∠D=90°-∠C=90°-35°=55°.2.如图,有一块含有60°
角的直角三角板的两个顶点放在矩形的对
边上.如果∠1=18°,那么∠2的度数是 .
【解析】如图,∵∠1+∠3=90°-60°=30°,
而∠1=18°,
∴∠3=30°-18°=12°,
∵AB∥CD,∴∠2=∠3=12°.
答案:12°3.如图,在△ABC中,∠ACB=
90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC
于点E,CF∥AB交DE的延长线于点F.连接CD,过
点D作DC的垂线交CF的延长线于点G.
求证:∠B=∠A+∠DGC.【证明】∵CF∥AB,∴∠A=∠ACG,
∴∠A+∠DGC=∠ACG+∠DGC=∠DHC,
∵∠ACB=90°,点D为边AB的中点,
∴AD=DC,∴∠A=∠ACD,
又∵∠ACB=∠CDG=90°,
∴∠B=∠DHC,∴∠B=∠A+∠DGC.考点 2 勾股定理及其逆定理
【知识点睛】
1.勾股定理的逆定理是研究三角形三边的数量关系的定理,利用勾股定理的逆定理判定一个三角形是否是直角三角形的一般步骤:
(1)判断哪条边最大.
(2)分别用代数方法计算出较小两边的平方和及最大边的平方的值.(3)判断它们是否相等,若相等,则是直角三角形;若不相等,则不是直角三角形.?2.勾股定理及其逆定理可以解决直角三角形中有关边、角的问题,在应用勾股定理的时候要注意以下三点:
(1)条件:勾股定理及其逆定理一定要在直角三角形中应用,或者先通过作辅助线构造直角三角形再进行应用.
(2)方法:在解决问题时,常用数形结合的方法.
(3)分类:分类讨论,要学会从不同角度考虑条件和图形,在讨论的过程中提高学生对知识的灵活应用能力.【例2】如图,一根长6 m的木棒AB,斜靠在
与地面OM垂直的墙ON上,与地面的倾斜角∠ABO=60°.当木棒A
端沿墙下滑至点A'时,B端沿地面向右滑行至点B'.
(1)求OB的长.
(2)当AA'=1m时,求BB'的长.【思路点拨】(1)先求出∠OAB=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出OB的长.
(2)先由勾股定理求出OA的长,再由勾股定理求出OB'的长,即可得到BB'的长.【自主解答】(1)∵∠ABO=60°,∠AOB=90°,
∴∠OAB=90°-∠ABO=90°-60°=30°,
∴OB=
(2)∵
∴OA=
∵OA′=OA-AA′,AA′=1 m,
∴OA′=8 m,
在Rt△A′OB′中,OB′=
∴BB′=OB′-OB=【中考集训】
1.若直角三角形的两直角边长为a,b,且满
足 +|b-4|=0,则该直角三角形的斜边长为_____.
【解析】∵ +|b-4|=0,
∴a2-6a+9=0,b-4=0,
解得a=3,b=4,
∵直角三角形的两直角边长为a,b,
∴该直角三角形的斜边长=
答案:52.如图,正方形ODBC中,OC=1,OA=OB,则数轴上点A表示的数是________.
【解析】∵OC=1, ∴OB= ∵OA=OB,
∴数轴上点A表示的数是
答案:3.如图,长方形ABCD中,E是BC的中点,长方形ABCD的周长是20 cm,AE=5 cm,则AB的长为______cm.【解析】设AB=x,则可得BC=10-x,
∵E是BC的中点,∴
在Rt△ABE中,AB2+BE2=AE2,
即
解得,x=4.
即AB的长为4 cm.
答案:44.如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).【解析】将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,如图,∵高为1.2 m,底面周长为1 m,在容器内壁离容器底部0.3 m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,
∴A′D=0.5 m,BD=1.2 m,
= =1.3(m).
答案:1.3考点 3 直角三角形全等的判定及应用?
【知识点睛】
1.判定两个直角三角形全等的基本思路:
(1)已知两边相等,用“HL”或“SAS”证明.
(2)已知一边、一角相等,用“ASA”或“AAS”证明.2.直角三角形全等的应用:
(1)证明线段或角相等.
(2)通过角的关系判断线和线之间的位置关系.【例3】如图,在△ABC中,
AB=CB,∠ABC=90°,D为AB延长线上一点,点
E在BC边上,且BE=BD,连接AE,DE,DC.
(1)求证:△ABE≌△CBD.
(2)若∠CAE=30°,求∠BDC的度数.【思路点拨】(1)求出∠ABE=∠CBD,然后利用“边角边”证明△ABE和△CBD全等即可.
(2)先根据等腰直角三角形的锐角都是45°求出∠CAB,再求出∠BAE,然后根据全等三角形对应角相等求出∠BCD,再根据直角三角形两锐角互余求解即可.【自主解答】(1)∵∠ABC=90°,D为AB延长线上一点,
∴∠ABE=∠CBD=90°,
在△ABE和△CBD中,
∴△ABE≌△CBD(SAS).(2)∵AB=CB,∠ABC=90°,
∴∠CAB=45°,
∵∠CAE=30°,
∴∠BAE=∠CAB-∠CAE=45°-30°=15°,
∵△ABE≌△CBD,
∴∠BCD=∠BAE=15°,
∴∠BDC=90°-∠BCD=90°-15°=75°.【中考集训】
1.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,
则AE= cm.【解析】∵∠ACB=90°,
∴∠ECF+∠BCD=90°,
∵CD⊥AB,
∴∠BCD+∠B=90°,
∴∠ECF=∠B,
在△ABC和△FCE中,
∵∠ECF=∠B,EC=BC,∠ACB=∠FEC=90°,
∴△ABC≌△FCE(ASA),∴AC=EF,
∵AE=AC-CE,BC=2cm,EF=5cm,
∴AE=5-2=3(cm).
答案:32.如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E.
求证:△ABC≌△MED.【证明】∵MD⊥AB,
∴∠MDE=∠C=90°,
∵ME∥BC,
∴∠B=∠MED,
在△ABC与△MED中,
∴△ABC≌△MED.3.如图,已知AD是△ABC的中线,分别过点B,C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.【证明】∵AD是△ABC的中线,
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BDE和△CDF中,
∴△BDE≌△CDF,∴BE=CF.考点 4 角平分线的性质?
【知识点睛】
角平分线性质的应用及注意事项:
1.应用:角平分线的性质是证明线段、角相等的重要依据.其成立的依据是全等三角形的性质.当与其他知识综合在一起时,主要考查角平分线性质的应用.
2.注意事项:应用性质及判定时,添加辅助线的方法一般是过角平分线上的一点作角两边的垂线.【例4】数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:小聪只带了直角三角板,他发现利用三角板也可以作角平分线,方法如下:小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是 .
(2)小聪的作法正确吗?请说明理由.
(3)请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)【思路点拨】(1)分析作法→作出判断
(2)证Rt△OPN≌Rt△OPM→作出判断
(3)用刻度尺构造全等三角形→相等的角【自主解答】(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是SSS,故答案为SSS.
(2)小聪的作法正确.
理由:∵PM⊥OM,PN⊥ON,
∴∠OMP=∠ONP=90°.在Rt△OMP和Rt△ONP中,
∵OP=OP,OM=ON,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP平分∠AOB.(3)如图所示
步骤:①利用刻度尺在OA,OB上分别截取OG=OH.
②连接GH,利用刻度尺作出GH的中点Q.
③作射线OQ,则OQ为∠AOB的平分线.【中考集训】
1.如图,已知OP平分∠AOB,
∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,
PE⊥OB于点E.如果点M是OP的中点,则DM的
长是( )【解析】选C.∵OP平分∠AOB,∠AOB=60°,
∴∠AOP=∠COP=30°,
∵CP∥OA,
∴∠AOP=∠CPO,
∴∠COP=∠CPO,
∴OC=CP=2,∵∠PCE=∠AOB=60°,PE⊥OB,
∴∠CPE=30°,
∴CE= CP=1,
∴PE=
∴OP=2PE=
∵PD⊥OA,点M是OP的中点,
∴2.如图,△ABC的三边AB,
BC,CA长分别为40,50,60.其三条角平分线
交于点O,则S△ABO∶S△BCO∶S△CAO= .【解析】过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,∵OA,OB,OC是△ABC的三条角平分线,
∴OD=OE=OF,
∵△ABC的三边AB,BC,CA的长
分别为40,50,60,
∴S△ABO∶S△BCO∶S△CAO
=
=AB∶BC∶AC=40∶50∶60=4∶5∶6.
答案:4∶5∶63.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,
则EF= .【解析】作EG⊥OA于G,
∵EF∥OB,
∴∠OEF=∠COE=15°,
∵∠AOE=15°,
∴∠EFG=15°+15°=30°,
∵EG=CE=1,
∴EF=2EG=2×1=2.
答案:24.如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.
(1)用尺规作图方法,作∠ADC的平分线DN.
(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状.(只写结果)【解析】(1)作出∠ADC的平分线DN如图所示.
(2)△ADF是等腰直角三角形.
第 1 章请写出框图中数字处的内容:
①_____________________;
②_____________________________________;
③___________________________________________________
___________________;
④_________________________________________________
________;
⑤___________________________________;直角三角形两锐角互余直角三角形斜边上的中线等于斜边的一半在直角三角形中,如果一个内角等于30°,那么它所对的直角边等于斜边的一半直角三角形两直角边a,b的平方和,等于斜边c的平方,即a2+b2=c2有一个角是直角的三角形是直角三角形⑥_________________________________;
⑦___________________________________________________
_________________;
⑧____________________________________________________
______________________________;
⑨_____________________________________;
⑩_____________________________________________.有两个角互余的三角形是直角三角形如果三角形的三边长a,b,c满足关系:a2+b2=c2,那么这个三角形是直角三角形斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”)角的平分线上的点到角的两边的距离相等角的内部到角的两边距离相等的点在角的平分线上考点 1 直角三角形判定与性质的应用
【知识点睛】
1.直角三角形的相关性质:2.直角三角形判定的选择思路:
(1)当题目中有角的度数时,用定义或有两个角互余的三角形是直角三角形来判定.
(2)当题目中有三个边的长度时,用勾股定理的逆定理判定.【例1】如图,已知两
个共一个顶点的等腰Rt△ABC,Rt△CEF,
∠ABC=∠CEF=90°,连接AF,M是AF的中
点,连接MB,ME.且CB与CE在同一直线上.
(1)求证MB∥CF.
(2)若AB=a,CE=2a,求BM,ME的长.【思路点拨】(1)连接CM,先由∠ACF=90°确定△ACF是直角三角形,可得AM=CM=FM,由SSS得△ABM≌△CBM,所以∠AMC=
2∠AMB=∠MFC+∠MCF,再由∠MFC=∠MCF得∠AMB=∠AFC,所以BM∥CF.
(2)由△CEM≌△FEM得出△EBM是等腰直角三角形,根据等腰直角三角形的性质求解即可.【自主解答】(1)如图,连接CM,
∵△ABC与△CEF是等腰直角三角形,∴∠ACF=2×45°=90°,
即△ACF是直角三角形,
又点M是AF的中点,
∴CM=AM,
又AB=CB,BM=BM,
∴△ABM≌△CBM,∴∠1=∠2,∴∠AMC=2∠1,
∵CM=MF,∴∠3=∠4,
∴∠AMC=2∠3,∴∠1=∠3,∴BM∥CF.(2)∵CM=FM,CE=FE,EM=EM,
∴△CEM≌△FEM,
∴∠CEM=∠FEM= ∠CEF=45°,
又由(1)可知BM∥CF,∴∠EBM=∠ECF=45°,
∴△EBM是等腰直角三角形,
∵AB=a,CE=2a,∴BE=2a-a=a,
又∵BM2+EM2=BE2,∴2BM2=2EM2=a2,
∴BM=EM= a.【中考集训】
1.如图,AB∥CD,
∠CED=90°,∠AEC=35°,则∠D的
大小为 ( )
A.65° B.55° C.45° D.35°
【解析】选B.∵AB∥CD,∴∠C=∠AEC=35°,
∵∠CED=90°,
∴∠D=90°-∠C=90°-35°=55°.2.如图,有一块含有60°
角的直角三角板的两个顶点放在矩形的对
边上.如果∠1=18°,那么∠2的度数是 .
【解析】如图,∵∠1+∠3=90°-60°=30°,
而∠1=18°,
∴∠3=30°-18°=12°,
∵AB∥CD,∴∠2=∠3=12°.
答案:12°3.如图,在△ABC中,∠ACB=
90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC
于点E,CF∥AB交DE的延长线于点F.连接CD,过
点D作DC的垂线交CF的延长线于点G.
求证:∠B=∠A+∠DGC.【证明】∵CF∥AB,∴∠A=∠ACG,
∴∠A+∠DGC=∠ACG+∠DGC=∠DHC,
∵∠ACB=90°,点D为边AB的中点,
∴AD=DC,∴∠A=∠ACD,
又∵∠ACB=∠CDG=90°,
∴∠B=∠DHC,∴∠B=∠A+∠DGC.考点 2 勾股定理及其逆定理
【知识点睛】
1.勾股定理的逆定理是研究三角形三边的数量关系的定理,利用勾股定理的逆定理判定一个三角形是否是直角三角形的一般步骤:
(1)判断哪条边最大.
(2)分别用代数方法计算出较小两边的平方和及最大边的平方的值.(3)判断它们是否相等,若相等,则是直角三角形;若不相等,则不是直角三角形.?2.勾股定理及其逆定理可以解决直角三角形中有关边、角的问题,在应用勾股定理的时候要注意以下三点:
(1)条件:勾股定理及其逆定理一定要在直角三角形中应用,或者先通过作辅助线构造直角三角形再进行应用.
(2)方法:在解决问题时,常用数形结合的方法.
(3)分类:分类讨论,要学会从不同角度考虑条件和图形,在讨论的过程中提高学生对知识的灵活应用能力.【例2】如图,一根长6 m的木棒AB,斜靠在
与地面OM垂直的墙ON上,与地面的倾斜角∠ABO=60°.当木棒A
端沿墙下滑至点A'时,B端沿地面向右滑行至点B'.
(1)求OB的长.
(2)当AA'=1m时,求BB'的长.【思路点拨】(1)先求出∠OAB=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出OB的长.
(2)先由勾股定理求出OA的长,再由勾股定理求出OB'的长,即可得到BB'的长.【自主解答】(1)∵∠ABO=60°,∠AOB=90°,
∴∠OAB=90°-∠ABO=90°-60°=30°,
∴OB=
(2)∵
∴OA=
∵OA′=OA-AA′,AA′=1 m,
∴OA′=8 m,
在Rt△A′OB′中,OB′=
∴BB′=OB′-OB=【中考集训】
1.若直角三角形的两直角边长为a,b,且满
足 +|b-4|=0,则该直角三角形的斜边长为_____.
【解析】∵ +|b-4|=0,
∴a2-6a+9=0,b-4=0,
解得a=3,b=4,
∵直角三角形的两直角边长为a,b,
∴该直角三角形的斜边长=
答案:52.如图,正方形ODBC中,OC=1,OA=OB,则数轴上点A表示的数是________.
【解析】∵OC=1, ∴OB= ∵OA=OB,
∴数轴上点A表示的数是
答案:3.如图,长方形ABCD中,E是BC的中点,长方形ABCD的周长是20 cm,AE=5 cm,则AB的长为______cm.【解析】设AB=x,则可得BC=10-x,
∵E是BC的中点,∴
在Rt△ABE中,AB2+BE2=AE2,
即
解得,x=4.
即AB的长为4 cm.
答案:44.如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).【解析】将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,如图,∵高为1.2 m,底面周长为1 m,在容器内壁离容器底部0.3 m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,
∴A′D=0.5 m,BD=1.2 m,
= =1.3(m).
答案:1.3考点 3 直角三角形全等的判定及应用?
【知识点睛】
1.判定两个直角三角形全等的基本思路:
(1)已知两边相等,用“HL”或“SAS”证明.
(2)已知一边、一角相等,用“ASA”或“AAS”证明.2.直角三角形全等的应用:
(1)证明线段或角相等.
(2)通过角的关系判断线和线之间的位置关系.【例3】如图,在△ABC中,
AB=CB,∠ABC=90°,D为AB延长线上一点,点
E在BC边上,且BE=BD,连接AE,DE,DC.
(1)求证:△ABE≌△CBD.
(2)若∠CAE=30°,求∠BDC的度数.【思路点拨】(1)求出∠ABE=∠CBD,然后利用“边角边”证明△ABE和△CBD全等即可.
(2)先根据等腰直角三角形的锐角都是45°求出∠CAB,再求出∠BAE,然后根据全等三角形对应角相等求出∠BCD,再根据直角三角形两锐角互余求解即可.【自主解答】(1)∵∠ABC=90°,D为AB延长线上一点,
∴∠ABE=∠CBD=90°,
在△ABE和△CBD中,
∴△ABE≌△CBD(SAS).(2)∵AB=CB,∠ABC=90°,
∴∠CAB=45°,
∵∠CAE=30°,
∴∠BAE=∠CAB-∠CAE=45°-30°=15°,
∵△ABE≌△CBD,
∴∠BCD=∠BAE=15°,
∴∠BDC=90°-∠BCD=90°-15°=75°.【中考集训】
1.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,
则AE= cm.【解析】∵∠ACB=90°,
∴∠ECF+∠BCD=90°,
∵CD⊥AB,
∴∠BCD+∠B=90°,
∴∠ECF=∠B,
在△ABC和△FCE中,
∵∠ECF=∠B,EC=BC,∠ACB=∠FEC=90°,
∴△ABC≌△FCE(ASA),∴AC=EF,
∵AE=AC-CE,BC=2cm,EF=5cm,
∴AE=5-2=3(cm).
答案:32.如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E.
求证:△ABC≌△MED.【证明】∵MD⊥AB,
∴∠MDE=∠C=90°,
∵ME∥BC,
∴∠B=∠MED,
在△ABC与△MED中,
∴△ABC≌△MED.3.如图,已知AD是△ABC的中线,分别过点B,C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.【证明】∵AD是△ABC的中线,
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BDE和△CDF中,
∴△BDE≌△CDF,∴BE=CF.考点 4 角平分线的性质?
【知识点睛】
角平分线性质的应用及注意事项:
1.应用:角平分线的性质是证明线段、角相等的重要依据.其成立的依据是全等三角形的性质.当与其他知识综合在一起时,主要考查角平分线性质的应用.
2.注意事项:应用性质及判定时,添加辅助线的方法一般是过角平分线上的一点作角两边的垂线.【例4】数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:小聪只带了直角三角板,他发现利用三角板也可以作角平分线,方法如下:小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是 .
(2)小聪的作法正确吗?请说明理由.
(3)请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)【思路点拨】(1)分析作法→作出判断
(2)证Rt△OPN≌Rt△OPM→作出判断
(3)用刻度尺构造全等三角形→相等的角【自主解答】(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是SSS,故答案为SSS.
(2)小聪的作法正确.
理由:∵PM⊥OM,PN⊥ON,
∴∠OMP=∠ONP=90°.在Rt△OMP和Rt△ONP中,
∵OP=OP,OM=ON,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP平分∠AOB.(3)如图所示
步骤:①利用刻度尺在OA,OB上分别截取OG=OH.
②连接GH,利用刻度尺作出GH的中点Q.
③作射线OQ,则OQ为∠AOB的平分线.【中考集训】
1.如图,已知OP平分∠AOB,
∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,
PE⊥OB于点E.如果点M是OP的中点,则DM的
长是( )【解析】选C.∵OP平分∠AOB,∠AOB=60°,
∴∠AOP=∠COP=30°,
∵CP∥OA,
∴∠AOP=∠CPO,
∴∠COP=∠CPO,
∴OC=CP=2,∵∠PCE=∠AOB=60°,PE⊥OB,
∴∠CPE=30°,
∴CE= CP=1,
∴PE=
∴OP=2PE=
∵PD⊥OA,点M是OP的中点,
∴2.如图,△ABC的三边AB,
BC,CA长分别为40,50,60.其三条角平分线
交于点O,则S△ABO∶S△BCO∶S△CAO= .【解析】过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,∵OA,OB,OC是△ABC的三条角平分线,
∴OD=OE=OF,
∵△ABC的三边AB,BC,CA的长
分别为40,50,60,
∴S△ABO∶S△BCO∶S△CAO
=
=AB∶BC∶AC=40∶50∶60=4∶5∶6.
答案:4∶5∶63.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,
则EF= .【解析】作EG⊥OA于G,
∵EF∥OB,
∴∠OEF=∠COE=15°,
∵∠AOE=15°,
∴∠EFG=15°+15°=30°,
∵EG=CE=1,
∴EF=2EG=2×1=2.
答案:24.如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.
(1)用尺规作图方法,作∠ADC的平分线DN.
(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状.(只写结果)【解析】(1)作出∠ADC的平分线DN如图所示.
(2)△ADF是等腰直角三角形.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
