27.2.3相似三角形应用举例 同步练习题及答案
文档属性
| 名称 | 27.2.3相似三角形应用举例 同步练习题及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 232.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 10:49:51 | ||
图片预览

文档简介
相似三角形应用举例同步练习题
一、选择题
1.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,
CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的
垂直距离CD为( )
A.0.2 m B.0.3 m C.0.4 m D.0.5 m
2.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好完全通过,请你根据图中数据回答,两层楼之间的高约为( )
A.5.5m B.6.2m C.11m D.2.2m
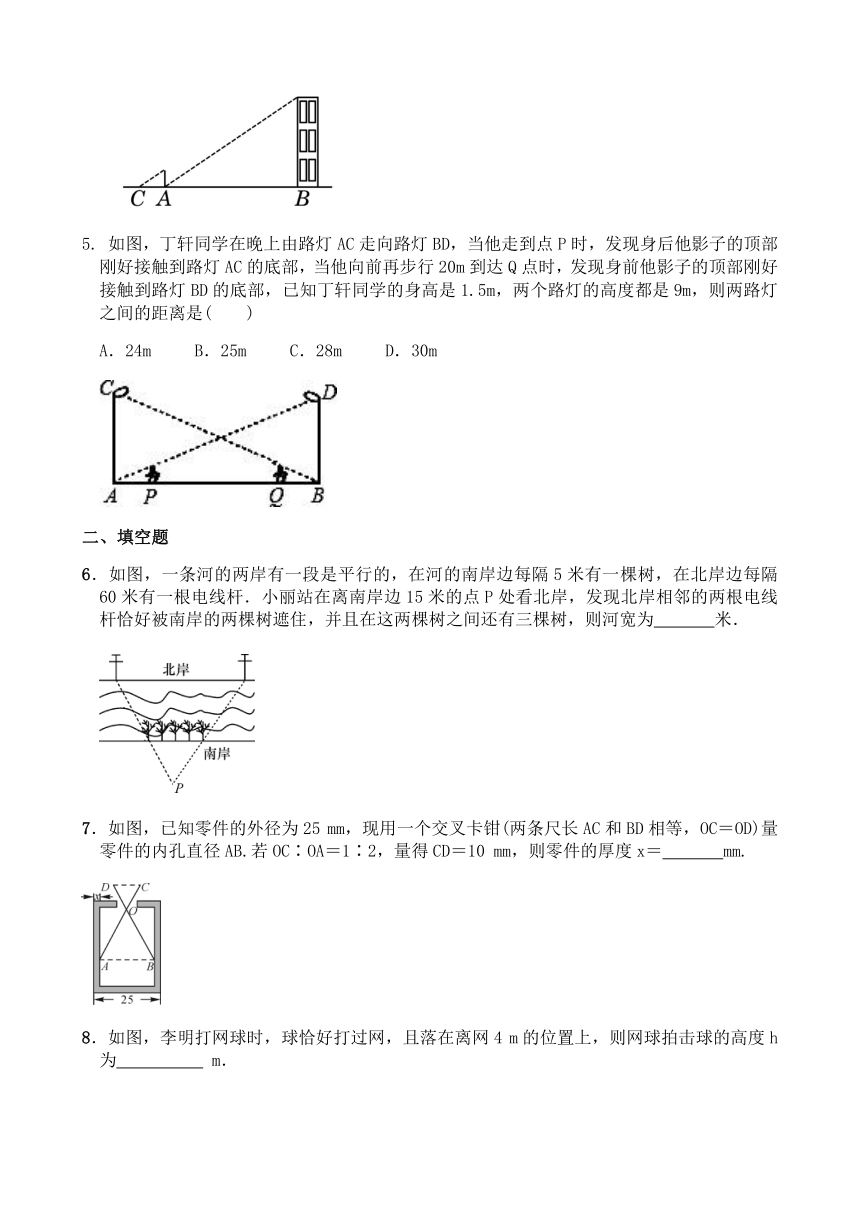
4. 小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.8米 B.10米 C.15米 D.22.5米
5. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )
A.24m B.25m C.28m D.30m
二、填空题
6.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.
7.如图,已知零件的外径为25 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x= mm.
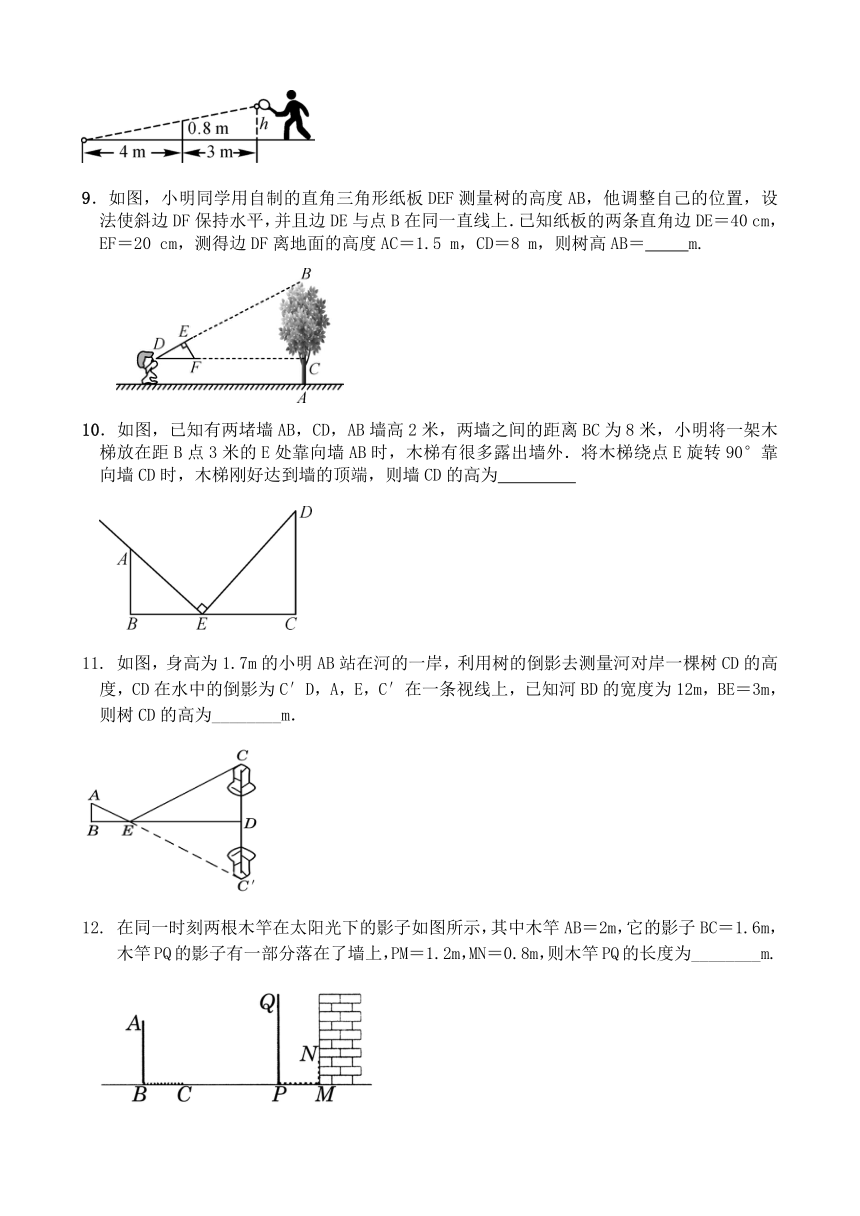
8.如图,李明打网球时,球恰好打过网,且落在离网4 m的位置上,则网球拍击球的高度h为 m.
9.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB= m.
10.如图,已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外.将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为
11. 如图,身高为1.7m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条视线上,已知河BD的宽度为12m,BE=3m,则树CD的高为________m.
12. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为________m.
三、解答题
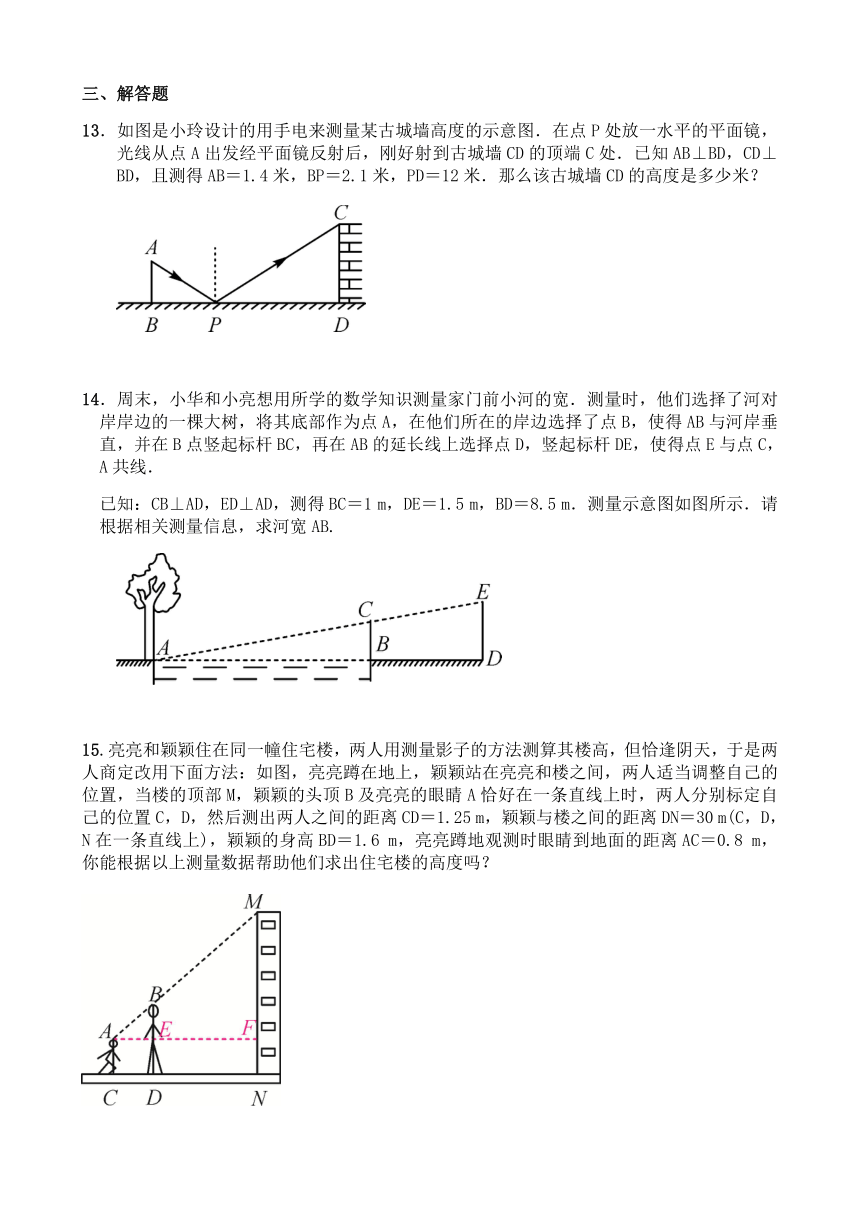
13.如图是小玲设计的用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是多少米?
14.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C,A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
15.亮亮和颖颖住在同一幢住宅楼,两人用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C,D,然后测出两人之间的距离CD=1.25 m,颖颖与楼之间的距离DN=30 m(C,D,N在一条直线上),颖颖的身高BD=1.6 m,亮亮蹲地观测时眼睛到地面的距离AC=0.8 m,你能根据以上测量数据帮助他们求出住宅楼的高度吗?
相似三角形应用举例同步练习题
一、选择题
1.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,
CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的
垂直距离CD为( C )
A.0.2 m B.0.3 m C.0.4 m D.0.5 m
2.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( B )
A.五丈 B.四丈五尺 C.一丈 D.五尺
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好完全通过,请你根据图中数据回答,两层楼之间的高约为( A )
A.5.5m B.6.2m C.11m D.2.2m
4. 小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( B )
A.8米 B.10米 C.15米 D.22.5米
5. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是(D )
A.24m B.25m C.28m D.30m
二、填空题
6.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 30 米.
7.如图,已知零件的外径为25 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x= 2.5 mm.
8.如图,李明打网球时,球恰好打过网,且落在离网4 m的位置上,则网球拍击球的高度h为 1.4 m.
9.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB= 5.5 m.
10.如图,已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外.将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为 7.5 米
11. 如图,身高为1.7m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条视线上,已知河BD的宽度为12m,BE=3m,则树CD的高为___5.1_____m.
12. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为__2.3______m.
三、解答题
13.如图是小玲设计的用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是多少米?
解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP.
∴=,即=.
解得CD=8.
答:该古城墙CD的高度是8米.
14.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C,A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
解:∵BC∥DE,∴△ABC∽△ADE.∴=.
设AB=x m,则=,解得x=17.
经检验,x=17是原分式方程的解.
答:河宽AB的长为17 m.
15.亮亮和颖颖住在同一幢住宅楼,两人用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C,D,然后测出两人之间的距离CD=1.25 m,颖颖与楼之间的距离DN=30 m(C,D,N在一条直线上),颖颖的身高BD=1.6 m,亮亮蹲地观测时眼睛到地面的距离AC=0.8 m,你能根据以上测量数据帮助他们求出住宅楼的高度吗?
解:过点A作CN的平行线交BD于点E,交MN于点F.
由已知可得,FN=ED=AC=0.8 m,AE=CD=1.25 m,EF=DN=30 m,BD=1.6 m,
∠AEB=∠AFM=90°.
又∵∠BAE=∠MAF,
∴△ABE∽△AMF.
∴=,
即=.
解得MF=20.
∴MN=MF+FN=20+0.8=20.8(m).
答:住宅楼的高度为20.8 m.
一、选择题
1.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,
CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的
垂直距离CD为( )
A.0.2 m B.0.3 m C.0.4 m D.0.5 m
2.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好完全通过,请你根据图中数据回答,两层楼之间的高约为( )
A.5.5m B.6.2m C.11m D.2.2m
4. 小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.8米 B.10米 C.15米 D.22.5米
5. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )
A.24m B.25m C.28m D.30m
二、填空题
6.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.
7.如图,已知零件的外径为25 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x= mm.
8.如图,李明打网球时,球恰好打过网,且落在离网4 m的位置上,则网球拍击球的高度h为 m.
9.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB= m.
10.如图,已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外.将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为
11. 如图,身高为1.7m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条视线上,已知河BD的宽度为12m,BE=3m,则树CD的高为________m.
12. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为________m.
三、解答题
13.如图是小玲设计的用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是多少米?
14.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C,A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
15.亮亮和颖颖住在同一幢住宅楼,两人用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C,D,然后测出两人之间的距离CD=1.25 m,颖颖与楼之间的距离DN=30 m(C,D,N在一条直线上),颖颖的身高BD=1.6 m,亮亮蹲地观测时眼睛到地面的距离AC=0.8 m,你能根据以上测量数据帮助他们求出住宅楼的高度吗?
相似三角形应用举例同步练习题
一、选择题
1.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,
CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的
垂直距离CD为( C )
A.0.2 m B.0.3 m C.0.4 m D.0.5 m
2.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( B )
A.五丈 B.四丈五尺 C.一丈 D.五尺
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好完全通过,请你根据图中数据回答,两层楼之间的高约为( A )
A.5.5m B.6.2m C.11m D.2.2m
4. 小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( B )
A.8米 B.10米 C.15米 D.22.5米
5. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是(D )
A.24m B.25m C.28m D.30m
二、填空题
6.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 30 米.
7.如图,已知零件的外径为25 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x= 2.5 mm.
8.如图,李明打网球时,球恰好打过网,且落在离网4 m的位置上,则网球拍击球的高度h为 1.4 m.
9.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB= 5.5 m.
10.如图,已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外.将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为 7.5 米
11. 如图,身高为1.7m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条视线上,已知河BD的宽度为12m,BE=3m,则树CD的高为___5.1_____m.
12. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为__2.3______m.
三、解答题
13.如图是小玲设计的用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是多少米?
解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP.
∴=,即=.
解得CD=8.
答:该古城墙CD的高度是8米.
14.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C,A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
解:∵BC∥DE,∴△ABC∽△ADE.∴=.
设AB=x m,则=,解得x=17.
经检验,x=17是原分式方程的解.
答:河宽AB的长为17 m.
15.亮亮和颖颖住在同一幢住宅楼,两人用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C,D,然后测出两人之间的距离CD=1.25 m,颖颖与楼之间的距离DN=30 m(C,D,N在一条直线上),颖颖的身高BD=1.6 m,亮亮蹲地观测时眼睛到地面的距离AC=0.8 m,你能根据以上测量数据帮助他们求出住宅楼的高度吗?
解:过点A作CN的平行线交BD于点E,交MN于点F.
由已知可得,FN=ED=AC=0.8 m,AE=CD=1.25 m,EF=DN=30 m,BD=1.6 m,
∠AEB=∠AFM=90°.
又∵∠BAE=∠MAF,
∴△ABE∽△AMF.
∴=,
即=.
解得MF=20.
∴MN=MF+FN=20+0.8=20.8(m).
答:住宅楼的高度为20.8 m.
