北师大版七年级数学下册第二章 相交线与平行线练习含答案
文档属性
| 名称 | 北师大版七年级数学下册第二章 相交线与平行线练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 558.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 21:49:58 | ||
图片预览



文档简介
第二章 相交线与平行线
一、单选题
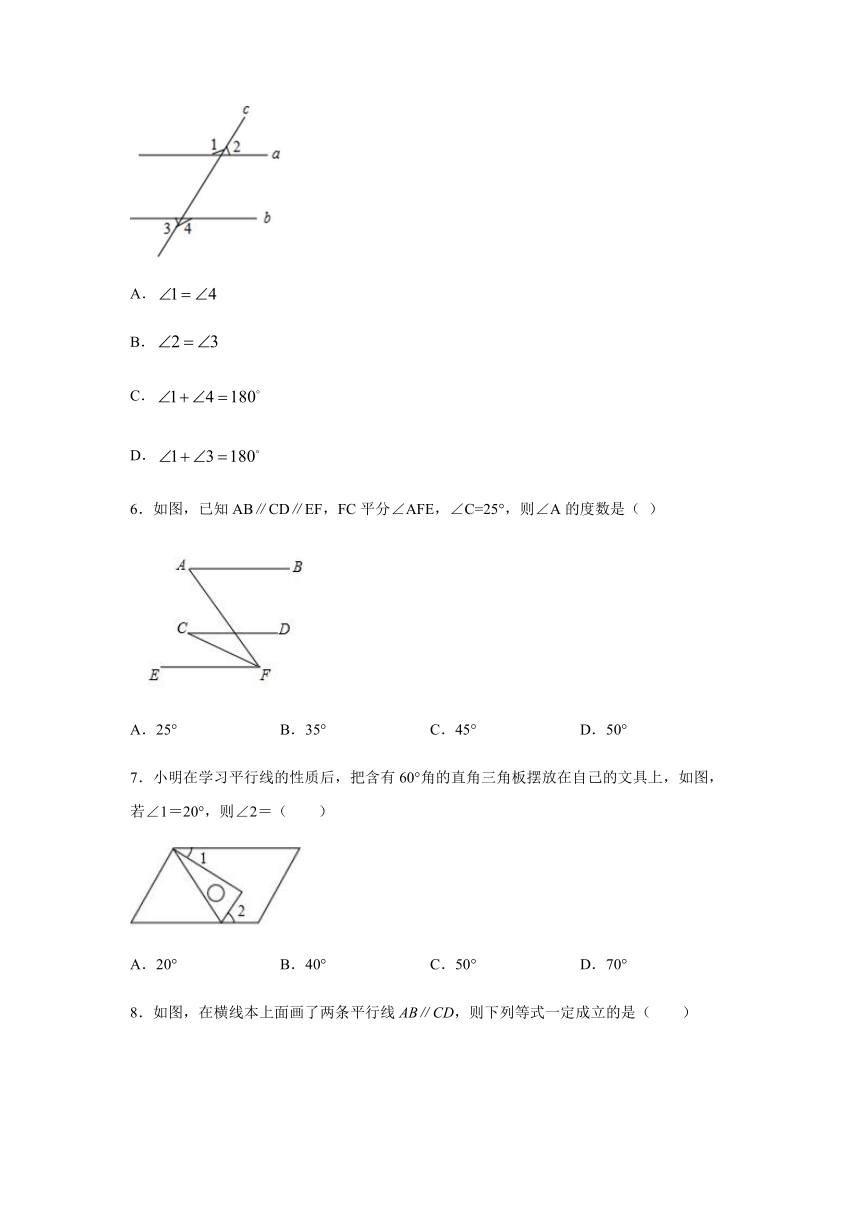
1.如图所示,两条直线相交于点,若,则( )
A. B. C. D.
2.如图,过点P画出直线AB的垂线.下列画法中,正确的是( )
A. B.
C. D.
3.下列图中,与是对内错角的是( )
A. B. C. D.
4.下列说法正确的是( )
A.同旁内角互补 B.在同一平面内,若a⊥b,b⊥c,则a⊥c
C.对顶角相等 D.一个角的补角一定是钝角
5.如图,直线a、b被直线c所截,下列条件中,不能判断直线a、b平行的是( )
A.
B.
C.
D.
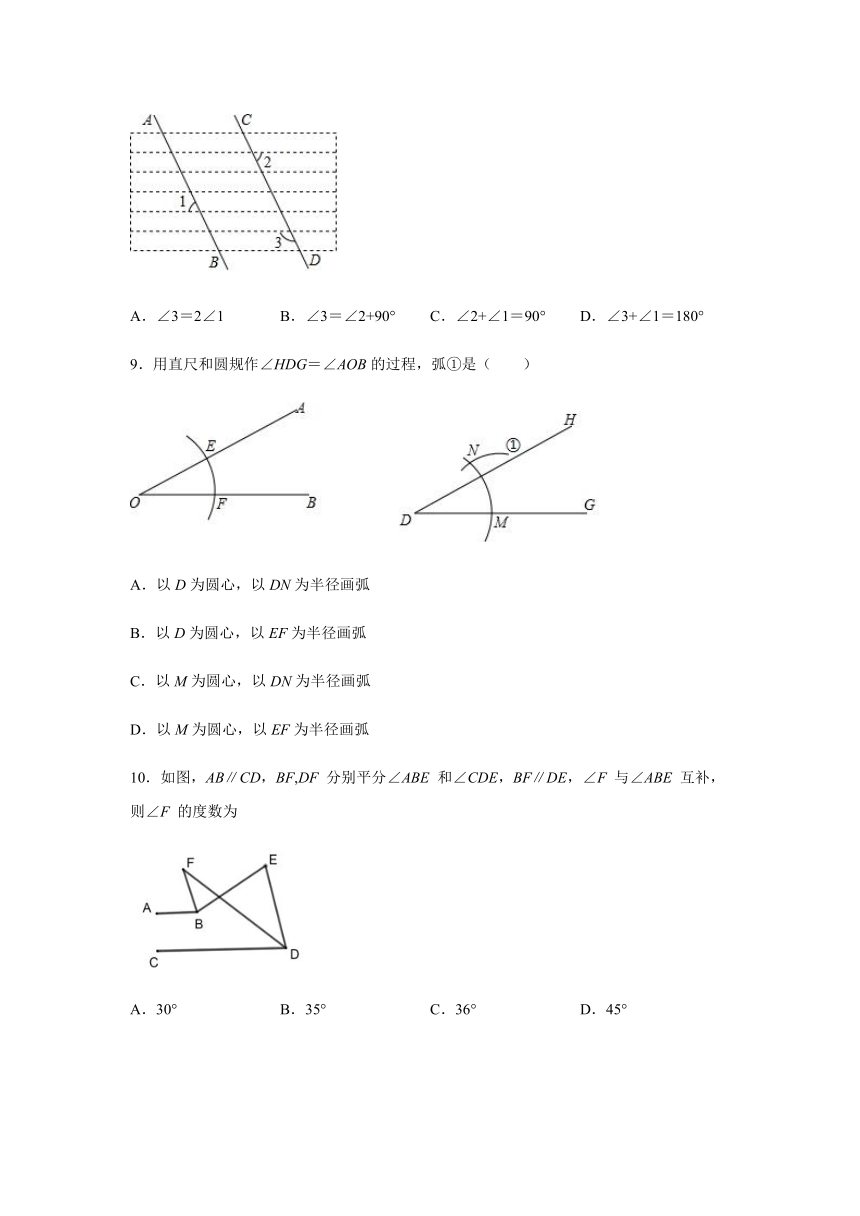
6.如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )
A.25° B.35° C.45° D.50°
7.小明在学习平行线的性质后,把含有60°角的直角三角板摆放在自己的文具上,如图,若∠1=20°,则∠2=( )
A.20° B.40° C.50° D.70°
8.如图,在横线本上面画了两条平行线AB∥CD,则下列等式一定成立的是( )
A.∠3=2∠1 B.∠3=∠2+90° C.∠2+∠1=90° D.∠3+∠1=180°
9.用直尺和圆规作∠HDG=∠AOB的过程,弧①是( )
A.以D为圆心,以DN为半径画弧
B.以D为圆心,以EF为半径画弧
C.以M为圆心,以DN为半径画弧
D.以M为圆心,以EF为半径画弧
10.如图,AB∥CD,BF,DF 分别平分∠ABE 和∠CDE,BF∥DE,∠F 与∠ABE 互补,则∠F 的度数为
A.30° B.35° C.36° D.45°
二、填空题
11.如图 ,∠1 与∠3 是直线_____与直线_____被直线 EF 所截的内错角,∠1 与∠2 是直线AB 与 CD 被直线 EF 所截的 ____________角,∠D 与∠1 是直线 EF 与 BD 被直线 CD 所截的____________________角.
12.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线的位置关系是_____.
13.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的是___(只填序号)
14.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是________
三、解答题
15.如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,证明:ON⊥CD;
(2)若,求∠BOD的度数.
16.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线,被直线所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线,,两两相交,交点分别为、、,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内条直线两两相交,最多可以形成______对同旁内角.
17.如图,已知直线EF分别与直线AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为O,∠AOP=30°.
(1)若∠CME=120°,问AB和CD平行吗?为什么?
(2)若直线AB∥CD,求∠EMD的度数.
18.如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.
解:因为∠1=∠2=80°(已知),
所以AB∥CD__________
所以∠BGF+∠3=180°__________
因为∠2+∠EFD=180°(邻补角的性质).
所以∠EFD=________.(等式性质).
因为FG平分∠EFD(已知).
所以∠3=________∠EFD(角平分线的性质).
所以∠3=________.(等式性质).
所以∠BGF=________.(等式性质).
19.在综合与实践课上,同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线且和直角三角形,,,.
操作发现:
(1)在如图1中,,求的度数;
(2)如图2,创新小组的同学把直线向上平移,并把的位置改变,发现,说明理由;
实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,平分,此时发现与又存在新的数量关系,请直接写出与的数量关系.
答案
1.B
2.A
3.A
4.C
5.C
6.D
7.D
8.D
9.D
10.C
11.AB CD 同旁内 同位
12.b//c
13.①④.
14.150°
15.(1)∵,∴,
∵∠1=∠2,∴
∴;
(2) ∵,∴,
∵
∴
∴∠
16.(1)如图
其中同旁内角有与,与,共2对
(2)如图
其中同旁内角有与,与,与,与,与,与,共6对,
(3)如图
其中的同位角有与,与,与,与,与,与,与,与,与,与,与,与,与,与,与,与, 与,与,与,与,与,与,与,与共24对,
(4)根据以上规律,平面内条直线两两相交,最多可以形成对同旁内角
17.(1)结论:AB∥CD.
理由:∵OP⊥OE,
∴∠POE=90°,
∵∠AOP=30°,
∴∠AOE=120°,
∵∠AME=120°,
∴∠AOE=∠CME,
∴AB∥CD.
(2)∵AB∥CD,
∴∠EMD=∠EOB,
∵∠EOB=180°-∠1OE=60°,
∴∠EMD=60°.
18.因为∠1=∠2=80°(已知), 所以AB∥CD(同位角相等,两直线平行),
所以∠BGF+∠3=180°(两直线平行,同旁内角互补),
因为∠2+∠EFD=180°(邻补角的性质),
所以∠EFD=100°(等式性质),
因为FG平分∠EFD(已知),
所以∠3= ∠EFD(角平分线的性质),
所以∠3=50°(等式性质),
所以∠BGF=130°(等式性质),
故答案为:同位角相等,两直线平行;两直线平行,同旁内角互补;100°; ;50°;130°.
19.(1)如图1,
∵∠BCA=90°,∠1=46°,
∴∠3=180°-∠BCA-∠1=44°,
∵a//b,
∴∠2=∠3=44°;
(2)理由如下:如图2,过点B作BD//a,
∴∠2+∠ABD=180°,
∵a//b,
∴b//BD,
∴∠1=∠DBC,
∴∠ABD=∠ABC-∠DBC=60°-∠1,
∴∠2+60°-∠1=180°,
∴∠2-∠1=120°;
(3)∠1=∠2,理由如下:如图3,过点C作CD//a,
∵AC平分∠BAM,
∴∠CAM=∠BAC=30°,∠BAM=2∠BAC=2×30°=60°,
∵CD//a,
∴∠BCD=∠2,
∵a//b,
∴∠1=∠BAM=60°,b//CD,
∴∠DCA=∠CAM=30°,
∵∠BCD=∠BCA-∠DCA,
∴∠BCD=90°-30°=60°,
∴∠2=60°,
∴∠1=∠2.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
