17.1 勾股定理同步练习题（含答案）

中小学教育资源及组卷应用平台


人教版八年级下册易错题专题
17.1 勾股定理
一．选择题（共9小题）
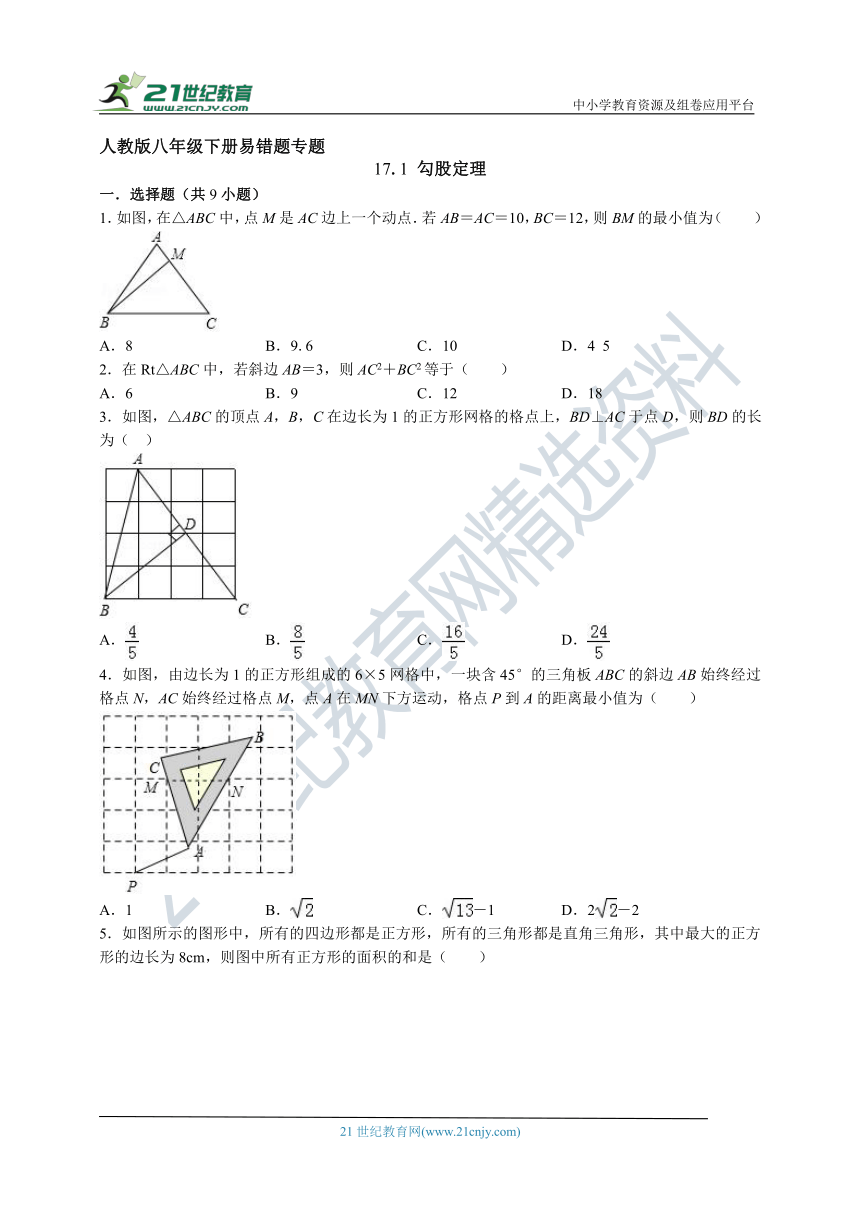
1．如图，在△ABC中，点M是AC边上一个动点．若AB＝AC＝10，BC＝12，则BM的最小值为（　　）

A．8 B．9.6 C．10 D．4 5
2．在Rt△ABC中，若斜边AB＝3，则AC2＋BC2等于（　　）
A．6 B．9 C．12 D．18
3．如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（ ）

A． B． C． D．
4．如图，由边长为1的正方形组成的6×5网格中，一块含45°的三角板ABC的斜边AB始终经过格点N，AC始终经过格点M，点A在MN下方运动，格点P到A的距离最小值为（　　）

A．1 B． C．－1 D．2－2
5．如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为8cm，则图中所有正方形的面积的和是（　　）

A．64 B．81 C．128 D．192
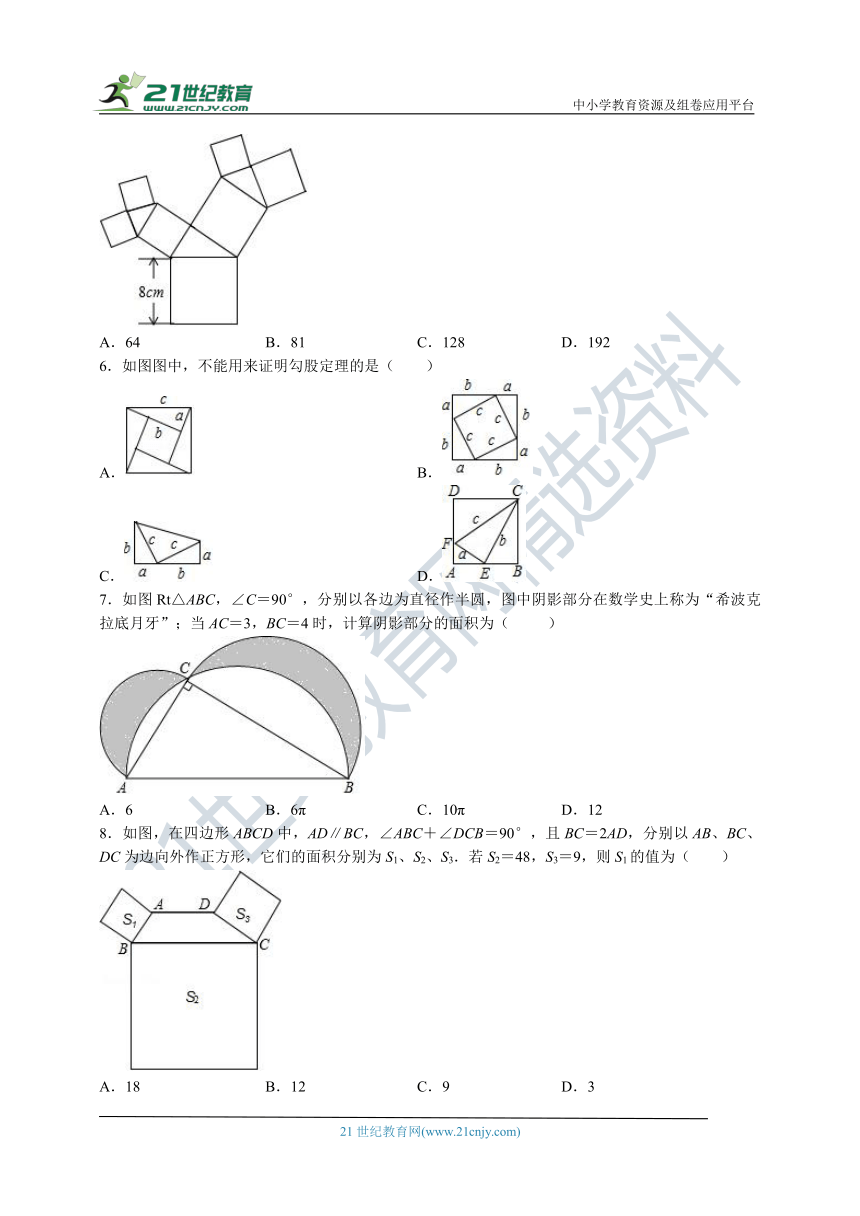
6．如图图中，不能用来证明勾股定理的是（　　）
A． B．
C． D．
7．如图Rt△ABC，∠C＝90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”；当AC＝3，BC＝4时，计算阴影部分的面积为（ ）

A．6 B．6π C．10π D．12
8．如图，在四边形ABCD中，AD∥BC，∠ABC＋∠DCB＝90°，且BC＝2AD，分别以AB、BC、DC为边向外作正方形，它们的面积分别为S1、S2、S3．若S2＝48，S3＝9，则S1的值为（　　）

A．18 B．12 C．9 D．3
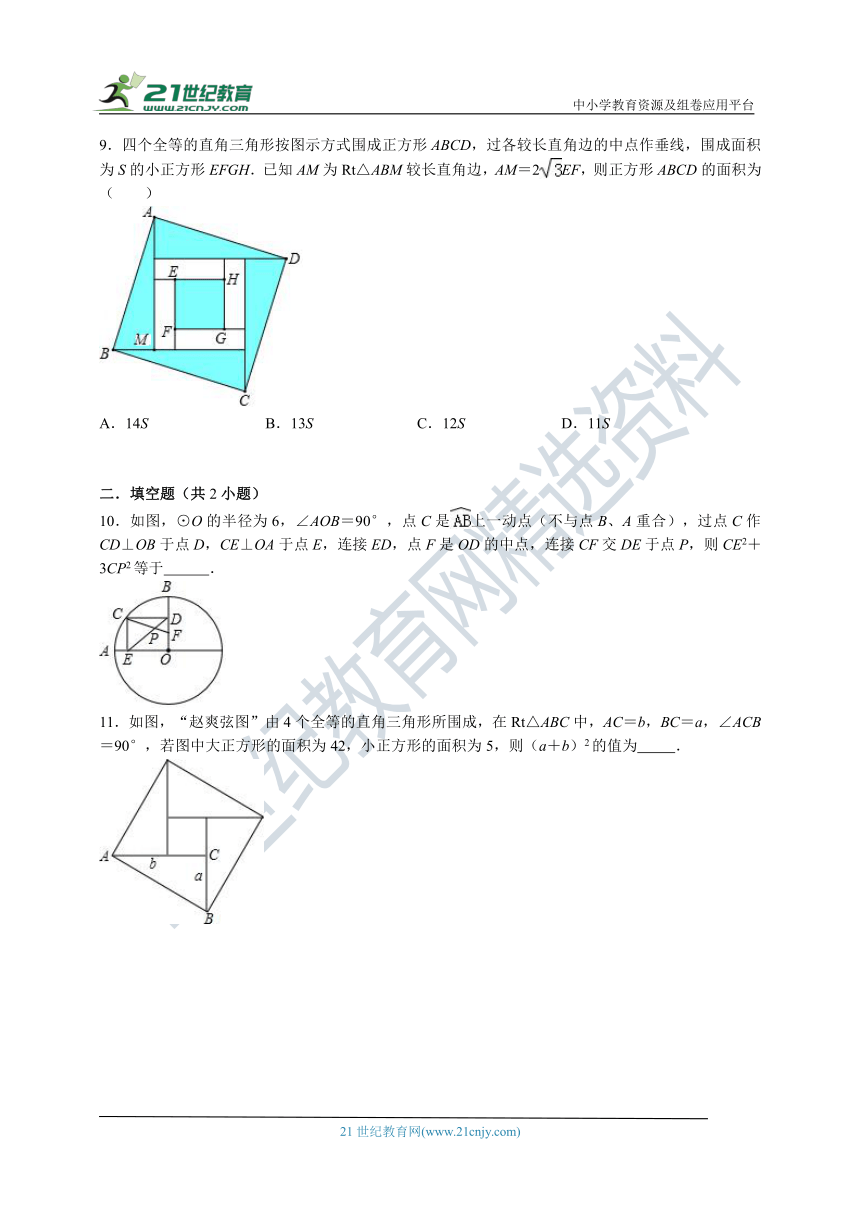
9．四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH．已知AM为Rt△ABM较长直角边，AM＝2EF，则正方形ABCD的面积为（　　）

A．14S B．13S C．12S D．11S


二．填空题（共2小题）
10．如图，⊙O的半径为6，∠AOB＝90°，点C是上一动点（不与点B、A重合），过点C作CD⊥OB于点D，CE⊥OA于点E，连接ED，点F是OD的中点，连接CF交DE于点P，则CE2＋3CP2等于 ．

11．如图，“赵爽弦图”由4个全等的直角三角形所围成，在Rt△ABC中，AC＝b，BC＝a，∠ACB＝90°，若图中大正方形的面积为42，小正方形的面积为5，则（a＋b）2的值为 ．








三．解答题（共5小题）
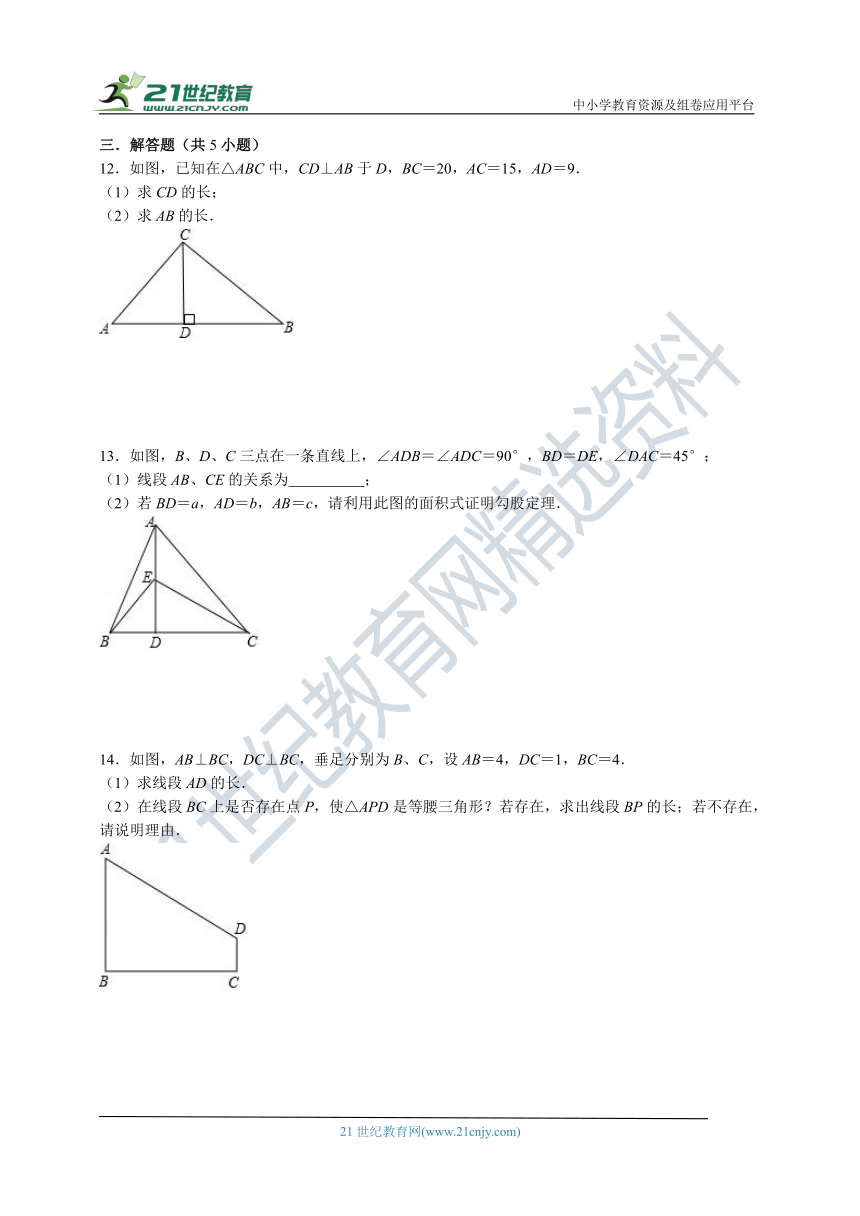
12．如图，已知在△ABC中，CD⊥AB于D，BC＝20，AC＝15，AD＝9．
（1）求CD的长；
（2）求AB的长．






13．如图，B、D、C三点在一条直线上，∠ADB＝∠ADC＝90°，BD＝DE，∠DAC＝45°；
（1）线段AB、CE的关系为 ；
（2）若BD＝a，AD＝b，AB＝c，请利用此图的面积式证明勾股定理．





14．如图，AB⊥BC，DC⊥BC，垂足分别为B、C，设AB＝4，DC＝1，BC＝4．
（1）求线段AD的长．
（2）在线段BC上是否存在点P，使△APD是等腰三角形？若存在，求出线段BP的长；若不存在，请说明理由．





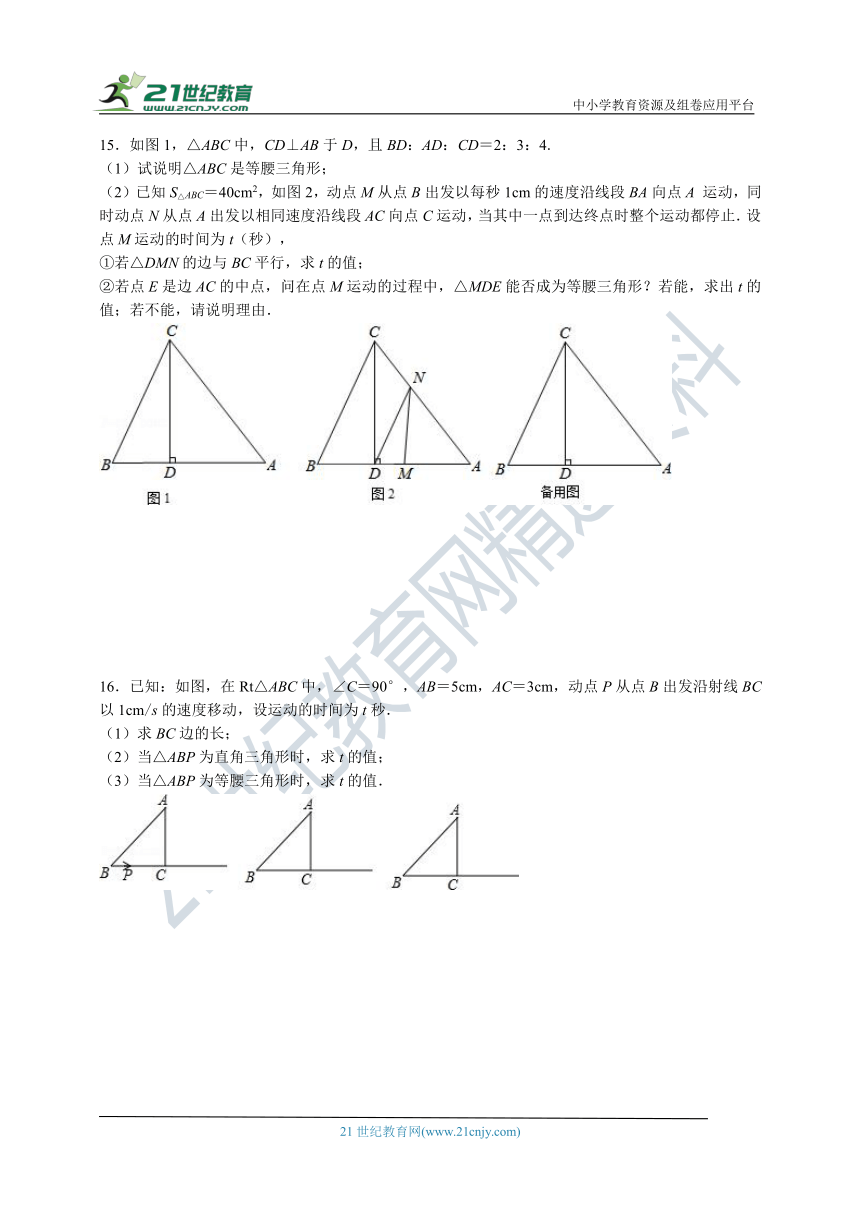
15．如图1，△ABC中，CD⊥AB于D，且BD：AD：CD＝2：3：4.
（1）试说明△ABC是等腰三角形；
（2）已知S△ABC＝40cm2，如图2，动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止．设点M运动的时间为t（秒），
①若△DMN的边与BC平行，求t的值；
②若点E是边AC的中点，问在点M运动的过程中，△MDE能否成为等腰三角形？若能，求出t的值；若不能，请说明理由．









16．已知：如图，在Rt△ABC中，∠C＝90°，AB＝5cm，AC＝3cm，动点P从点B出发沿射线BC以1cm/s的速度移动，设运动的时间为t秒．
（1）求BC边的长；
（2）当△ABP为直角三角形时，求t的值；
（3）当△ABP为等腰三角形时，求t的值．







参考答案及详细解析
一.选择题
1.答案：B.
解：作AD⊥BC于D，如图所示：

则∠ADB＝90°，
∵AB＝AC，
∴BD＝BC＝6，
由勾股定理得：AD＝＝8，
当BM⊥AC时，BM最小，
此时，∠BMC＝90°，
∵△ABC的面积＝AC?BM＝BC?AD，
即×10×BM＝×12×8，
解得：BM＝9.6，
故选：B．
2.答案：B.
解：∵Rt△ABC中，AB为斜边，
∴AC2＋BC2＝AB2，
∴AB2＋AC2＝AB2＝32＝9．
故选：B．
3.解：如图所示：
S△ABC＝×BC×AE＝×BD×AC，
∵AE＝4，AC＝＝5，BC＝4
即×4×4＝×5×BD，
解得：BD＝．
故选：C．

4.答案：B.
解：当AC与CM重合，AB与BN重合时，格点P到A的距离最小，由运动可得：点A的轨迹为圆弧，

此时PA＝，
故选：B．
5.答案：D.
解：∵所有的三角形都是直角三角形，所有的四边形都是正方形，

∴正方形A的面积＝a2，正方形B的面积＝b2，
正方形C的面积＝c2，正方形D的面积＝d2，
又∵a2＋b2＝x2，c2＋d2＝y2，
∴正方形A、B、C、D的面积和＝（a2＋b2）＋（c2＋d2）＝x2＋y2＝82＝64（cm2），
则所有正方形的面积的和是：64×3＝192（cm2）．
故选：D．
6.答案：D.
解：A，B，C都可以利用图形面积得出a，b，c的关系，即可证明勾股定理；故A，B，C选项不符合题意；
D、不能利用图形面积证明勾股定理，故此选项正确．
故选：D．
7.答案：A.
解：在Rt△ACB中，∠ACB＝90°，AC＝3，BC＝4，由勾股定理得：AB＝＝＝5，
所以阴影部分的面积S＝×π×（）2＋×（）2＋－×π×（）2＝6，
故选：A．
8.答案：D.
解：∵S2＝48，
∴BC＝4，
过A作AH∥CD交BC于H，

则∠AHB＝∠DCB，
∵AD∥BC，
∴四边形AHCD是平行四边形，
∴CH＝BH＝AD＝2，AH＝CD＝3，
∵∠ABC＋∠DCB＝90°，
∴∠AHB＋∠ABC＝90°，
∴∠BAH＝90°，
∴AB2＝BH2－AH2＝3，
∴S1＝3，
故选：D．
9.答案：B.
解：设AM＝2a．BM＝b．则正方形ABCD的面积＝4a2＋b2

由题意可知EF＝（2a－b）－2（a－b）＝2a－b－2a＋2b＝b，
∵AM＝2EF，
∴2a＝2b，
∴a＝b，
∵正方形EFGH的面积为S，
∴b2＝S，
∴正方形ABCD的面积＝4a2＋b2＝13b2＝13S，
故选：B．
二.填空题
10.解：设DF＝OF＝a，CD＝b，连接OC．

∵CD⊥OB于点D，CE⊥OA于点E，
∴∠EOD＝∠CDO＝∠CEO＝90°，
∴四边形CDOE是矩形，
∴CE＝OD＝2a，CD＝OE＝b，
∵EC∥DF，
∴＝＝，
∴PC＝2PF，PC＝CF＝，
∴EC2＋3CP2＝4a2＋（a2＋b2）＝（4a2＋b2），
在Rt△OCE中，∵EC2＋OE2＝OC2，
∴4a2＋b2＝36，
∴EC2＋3CP2＝48．
故答案为48

11.解：由图可知，（b－a）2＝5，
4×ab＝42－5＝37，
∴2ab＝37，
（a＋b）2＝（b－a）2＋4ab＝5＋2×37＝79．
故答案为79．


三.解答题
12.解：（1）在Rt△ACD中，CD＝＝12；
（2）在Rt△BCD中，BD＝＝16，
则AB＝AD＋BD＝25．
13.解（1）线段AB、CE的关系为：AB＝CE，AB⊥CE，
理由是：延长CE交AB于F，
∵∠ADC＝90°，∠DAC＝45°，
∴∠ACD＝∠DAC＝45°，
∴AD＝CD，
在△ADB和△CDE中，
∵，
∴△ADB≌△CDE（SAS），
∴AB＝CE，∠BAD＝∠DCE，
∵∠BAD＋∠ABD＝90°，
∴∠DCE＋∠ABD＝90°，
∴∠BFC＝90°，
∴AB⊥CE；
故答案为：AB＝CE，AB⊥CE．
（2）如图，设EF＝x，
∵S△ABC＝S△ABE＋S△BDE＋S△ACD，
∴＝AB?EF＋BD?DE＋DC?AD，
∵BD＝a，AB＝c，AD＝b，
∴易得 AB＝CE＝c，BD＝DE＝a，AD＝CD＝b，
∴cx＋a2＋，
即：＋cx＝cx＋a2＋，
∴，
∴a2＋b2＝c2.


14. 解：（1）如图1，过D作DE⊥AB于E点，

AE＝4－1＝3，DE＝BC＝4，
在Rt△AED中，AD＝＝5；
（2）如图2，

当AP＝AD时，
在Rt△ABP中，BP＝＝3；
如图3，

当PA＝PD时，
AB2＋BP2＝CD2＋（BC－BP）2，即42＋BP2＝12＋（4－BP）2，
解得BP＝．
综上所述，线段BP的长是3或．

15. 解：（1）证明：设BD＝2x，AD＝3x，CD＝4x，
则AB＝5x，
在Rt△ACD中，AC＝＝5x，
∴AB＝AC，
∴△ABC是等腰三角形；
（2）解：S△ABC＝×5x×4x＝40cm2，而x＞0，
∴x＝2cm，
则BD＝4cm，AD＝6cm，CD＝8cm，AC＝10cm．
①当MN∥BC时，AM＝AN，
即10－t＝t，
∴t＝5；
当DN∥BC时，AD＝AN，
得：t＝6；
∴若△DMN的边与BC平行时，t值为5或6．
②当点M在BD上，即0≤t＜4时，△MDE为钝角三角形，但DM≠DE；
当t＝4时，点M运动到点D，不构成三角形
当点M在DA上，即4＜t≤10时，△MDE为等腰三角形，有3种可能．
如果DE＝DM，则t－4＝5，
∴t＝9；
如果ED＝EM，则点M运动到点A，
∴t＝10；
如果MD＝ME＝t－4，
过点E做EF垂直AB于F，
因为ED＝EA，
所以DF＝AF＝AD＝3，
在Rt△AEF中，EF＝4；
因为BM＝t，BF＝7，
所以FM＝t－7
则在Rt△EFM中，（t－4）2－（t－7）2＝42，
∴t＝．
综上所述，符合要求的t值为9或10或．

16.解：（1）在Rt△ABC中，BC2＝AB2－AC2＝52－32＝16，
∴BC＝4（cm）；
（2）由题意知BP＝tcm，
①当∠APB为直角时，点P与点C重合，BP＝BC＝4cm，即t＝4；
②当∠BAP为直角时，BP＝tcm，CP＝（t－4）cm，AC＝3cm，
在Rt△ACP中，
AP2＝32＋（t－4）2，
在Rt△BAP中，AB2＋AP2＝BP2，
即：52＋[32＋（t－4）2]＝t2，
解得：t＝，
故当△ABP为直角三角形时，t＝4或t＝；
（3）①当AB＝BP时，t＝5；
②当AB＝AP时，BP＝2BC＝8cm，t＝8；
③当BP＝AP时，AP＝BP＝tcm，CP＝（4－t）cm，AC＝3cm，
在Rt△ACP中，AP2＝AC2＋CP2，
所以t2＝32＋（4－t）2，
解得：t＝，
综上所述：当△ABP为等腰三角形时，t＝5或t＝8或t＝．












21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)