人教版八年级上册数学11.2.1-三角形内角和(21张PPT)
文档属性
| 名称 | 人教版八年级上册数学11.2.1-三角形内角和(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 527.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 11:14:42 | ||
图片预览





文档简介
(共21张PPT)
11.2与三角形有关的角
11.2.1三角形角内角和
三角形蓝和三角形红见面了,
蓝炫耀的说:“我的面积比你大,
所以我的内角和也比你大!”
红不服气的说:“那可不好说噢,
你自己量量看!”
蓝用量角器量了量自己和红,就不再说话了!
同学们,你们知道其中的道吗?
情景引入
你的三边之和。是比我长,但三个内角之和并不比我大
我不但三边之和比你长,而且三个内角之和也比你大!
你同意谁的说法呢?为什么?
问题:
小学我们都已经知道三角形的三个内角和为180度,你还记得是怎么验证的吗?
想一想
三角形的三个内角和是180°
你有什么办法可以验证它呢?
方法一:通过具体的度量,验证三角形的内角和为180°.
方法二:剪拼法.把三个角拼在一起试试看?
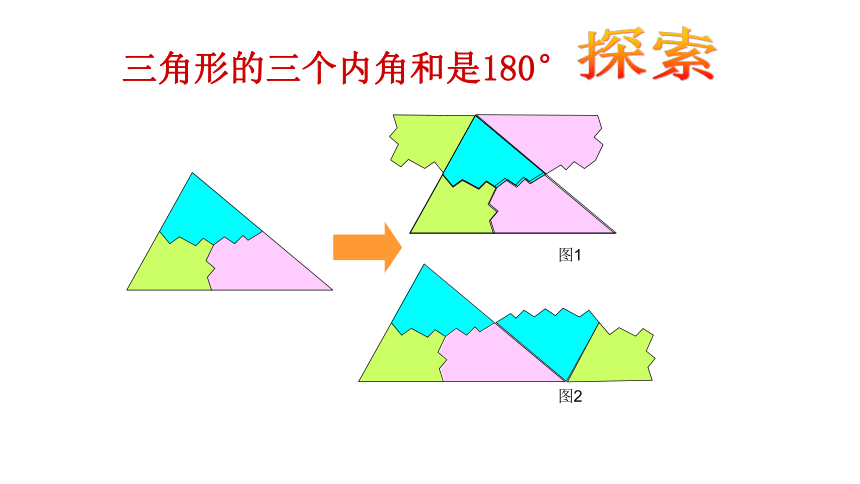
三角形的三个内角和是180°
图1
图2
探索
想一想
问题:有哪些方法可以得到180°
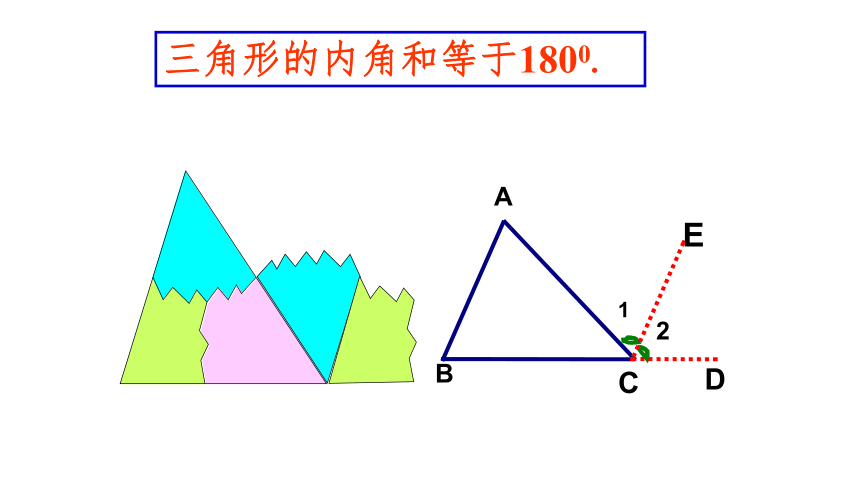
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
从刚才拼角的过程你能想出证明的方法吗?
3.邻补角的和是180 °
2
1
E
D
C
B
A
三角形的内角和等于1800.
“行家”
看“门道”
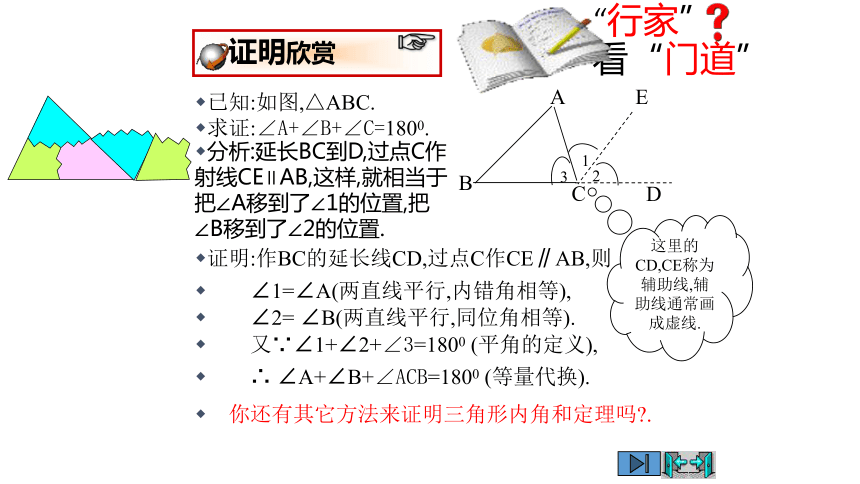
已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.
证明:作BC的延长线CD,过点C作CE∥AB,则
证明欣赏
?
你还有其它方法来证明三角形内角和定理吗?.
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3=1800 (平角的定义),
∴ ∠A+∠B+∠ACB=1800 (等量代换).
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
C
B
E
A
三角形的内角和等于1800.
定理证明
已知:△ABC
求证:∠A+∠B+∠C=1800
证明:过A作 EF∥BC
E
F
A
B
C
1
2
∵EF∥BC
∴∠B=∠1 ∠C=∠2
∴ ∠BAC +∠B+ ∠C= 1800
(两直线平行,内错角相等)
∵∠BAC + ∠1+ ∠2=1800
(等量代换)
“行家”
看“门道”
根据下面的图形,写出相应的证明.
试一试
?
你还能想出其它证法吗?
(1)
A
B
C
P
Q
R
T
S
N
(2)
A
B
C
P
Q
R
M
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
三种语言
?
A
B
C
新知应用
1、(1) 在△ABC中,∠C=90°,∠B=50 ° ,
则∠A=___。
(2)直角△ABC中, ∠A=5∠B,则∠C=_。
(3)等腰△ABC中, ∠A=4∠B, 则∠C=_。
2、证明:四边形的内角和为360o.
比一比,赛一赛
看哪一组做得又对又快!
我是最棒的
1.直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请说明你的结论.
三角形内角和应用
?
D
C
B
A
E
A
B
C
A
B
C
结论: 直角三角形的两个锐角互余.反过来两锐角互余的三角形是直角三角形。以后可以直接运用.
www.xkb1.com
3.如果等腰三角形的一角为100°,
则另两角分别为___________
如果等腰三角形的一角为70°,
则另两角分别为____________
40°、40°
55°、55°或70 °、40 °
提高训练
提示:等腰三角形的两条腰相等,两个底角相等。
即 在 △ABC, AB = AC,∠ABC = ∠ACB。
4.(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
5、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一 样的玻璃,那么最省事的办法是 ( )
带①去 (B)带②去
(C)带③去 (D)带①和②去
c
思考题:
如图,已知∠AMN+∠MNF+∠NFC=360°,
求证:AB∥CD(用两种方法证明)
D
F
N
M
B
A
C
学习了本节课你有哪些 收获?
课堂总结
1.三角形的内角和定理
2.推论1:直角三角形两锐角互余
推论2:两锐角互余的三角形是直角三角形
∠A + ∠B+ ∠C=180
?
结束寄语
严格性之于数学家,犹如道德之于人.
由“因”导“果”,执“果”索“因”.是探索证明思路的基本方法.
下课了!
再 见
11.2与三角形有关的角
11.2.1三角形角内角和
三角形蓝和三角形红见面了,
蓝炫耀的说:“我的面积比你大,
所以我的内角和也比你大!”
红不服气的说:“那可不好说噢,
你自己量量看!”
蓝用量角器量了量自己和红,就不再说话了!
同学们,你们知道其中的道吗?
情景引入
你的三边之和。是比我长,但三个内角之和并不比我大
我不但三边之和比你长,而且三个内角之和也比你大!
你同意谁的说法呢?为什么?
问题:
小学我们都已经知道三角形的三个内角和为180度,你还记得是怎么验证的吗?
想一想
三角形的三个内角和是180°
你有什么办法可以验证它呢?
方法一:通过具体的度量,验证三角形的内角和为180°.
方法二:剪拼法.把三个角拼在一起试试看?
三角形的三个内角和是180°
图1
图2
探索
想一想
问题:有哪些方法可以得到180°
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
从刚才拼角的过程你能想出证明的方法吗?
3.邻补角的和是180 °
2
1
E
D
C
B
A
三角形的内角和等于1800.
“行家”
看“门道”
已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.
证明:作BC的延长线CD,过点C作CE∥AB,则
证明欣赏
?
你还有其它方法来证明三角形内角和定理吗?.
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3=1800 (平角的定义),
∴ ∠A+∠B+∠ACB=1800 (等量代换).
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
C
B
E
A
三角形的内角和等于1800.
定理证明
已知:△ABC
求证:∠A+∠B+∠C=1800
证明:过A作 EF∥BC
E
F
A
B
C
1
2
∵EF∥BC
∴∠B=∠1 ∠C=∠2
∴ ∠BAC +∠B+ ∠C= 1800
(两直线平行,内错角相等)
∵∠BAC + ∠1+ ∠2=1800
(等量代换)
“行家”
看“门道”
根据下面的图形,写出相应的证明.
试一试
?
你还能想出其它证法吗?
(1)
A
B
C
P
Q
R
T
S
N
(2)
A
B
C
P
Q
R
M
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
三种语言
?
A
B
C
新知应用
1、(1) 在△ABC中,∠C=90°,∠B=50 ° ,
则∠A=___。
(2)直角△ABC中, ∠A=5∠B,则∠C=_。
(3)等腰△ABC中, ∠A=4∠B, 则∠C=_。
2、证明:四边形的内角和为360o.
比一比,赛一赛
看哪一组做得又对又快!
我是最棒的
1.直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请说明你的结论.
三角形内角和应用
?
D
C
B
A
E
A
B
C
A
B
C
结论: 直角三角形的两个锐角互余.反过来两锐角互余的三角形是直角三角形。以后可以直接运用.
www.xkb1.com
3.如果等腰三角形的一角为100°,
则另两角分别为___________
如果等腰三角形的一角为70°,
则另两角分别为____________
40°、40°
55°、55°或70 °、40 °
提高训练
提示:等腰三角形的两条腰相等,两个底角相等。
即 在 △ABC, AB = AC,∠ABC = ∠ACB。
4.(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
5、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一 样的玻璃,那么最省事的办法是 ( )
带①去 (B)带②去
(C)带③去 (D)带①和②去
c
思考题:
如图,已知∠AMN+∠MNF+∠NFC=360°,
求证:AB∥CD(用两种方法证明)
D
F
N
M
B
A
C
学习了本节课你有哪些 收获?
课堂总结
1.三角形的内角和定理
2.推论1:直角三角形两锐角互余
推论2:两锐角互余的三角形是直角三角形
∠A + ∠B+ ∠C=180
?
结束寄语
严格性之于数学家,犹如道德之于人.
由“因”导“果”,执“果”索“因”.是探索证明思路的基本方法.
下课了!
再 见
