2020春湘教版九下数学第2章圆2.2圆心角圆周角教学课件(29张PPT)
文档属性
| 名称 | 2020春湘教版九下数学第2章圆2.2圆心角圆周角教学课件(29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 801.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 13:40:57 | ||
图片预览








文档简介
课件29张PPT。教学课件
数学 九年级下册 湘教版
第2章 圆
2.2 圆心角、圆周角圆心角1、圆的概念是什么?2、圆的对称性:圆上任意两点间的部分叫作圆弧,简称弧.如图圆O上两点A,B间的小于半圆的部分
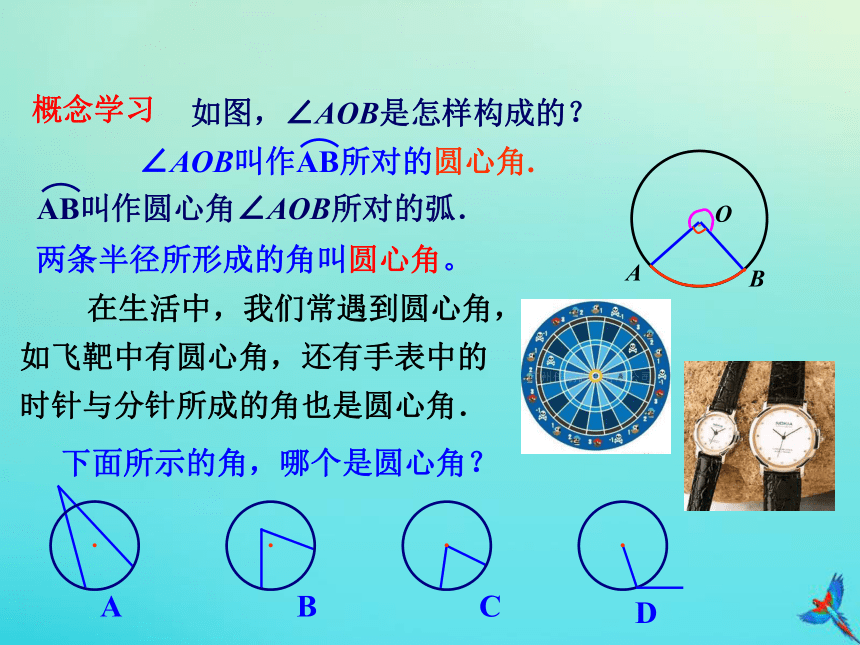
叫作劣弧,用符号“⌒”表示.A,B间的大于半圆的部分叫作优弧,圆是中心对称图形,圆心是它的对称中心。·O如图,∠AOB是怎样构成的?两条半径所形成的角叫圆心角。 在生活中,我们常遇到圆心角,
如飞靶中有圆心角,还有手表中的
时针与分针所成的角也是圆心角.下面所示的角,哪个是圆心角?概念学习圆心角、弦、弧的关系1、实验操作:在两张透明的纸上,分别作半径相等的⊙O和⊙O',
在⊙O和⊙O'中,作圆心角∠AOB和∠A'O'B',
连接AB和A'B',将两张纸重叠,
使⊙O和⊙O'重合。当∠AOB=∠A'O'B'时,弦AB A'B',2、探究思考:==3、在同一圆中,∠AOB=∠COD
由旋转不变性得:AB=CD,∠AOB=∠COD结论:在同圆或等圆中,如果圆心角相等,
那么它们所对的弧相等,所对的弦也相等.·OCBDA议一议 在同圆或等圆中,如果弦相等,那么它们所对的圆心角相等吗?所对的弧相等吗?你能讲出道理吗? 在同圆或等圆中,如果弧相等,那么它们所对的圆心角相等吗?所对的弦也相等吗?你能讲出道理吗?∠AOB=∠CODAB=CD∠AOB=∠CODAB=CD在同圆或等圆中,
如果两个圆心角,两条弧,两条弦中有一组量相等,
那么它们所对应的其余各组都分别相等。no的圆心角对着no的弧,
no的弧对着no的圆心角。圆心角的度数与它所对弧的度数相等。小知识2、已知⊙O的半径是5 cm,弦AB长是5 cm,则圆心角∠AOB= .60o35o解:连结CD,∠A=90o-28o=62o∠ACD=180o-62o×2=56o∠ECD=34o提示:证明?AOD、?DOC、?COB是
等边三角形,∠DCB=120o∠EOB=40o,∠AOC=∠COE=∠DOB=70o∠AOD=110o6、如图,已知CD是⊙O直径,圆心角∠AOB=30o,
弦CA//OB,求∠BOD的度数。7、如图,AB是⊙O直径,AC=CD,∠COD=60o,
(1)求证:?AOC是等边三角形。
(2)求证:OC//BD由CA//OB,∠AOB=30o,
得∠CAO=∠ACO=30o ∴∠AOC=120o∴∠AOD=60o∴∠BOD=30o(1)仿第4题得证(2)?AOC≌?BOD∴∠AOC=∠DBO=60o∴OC//BD1.圆是中心对称图形,圆心是它的对称中心。2.在同圆或等圆中,
如果两个圆心角,两条弧,两条弦中有一组量相等,
那么它们所对应的其余各组都分别相等。3.圆心角的度数与它所对弧的度数相等。练 习 巩 固:练习第1、2题作 业 布 置:
习题2.2第1、2题圆周角(1)3、如图,已知∠BOC=80°, ①求AB弧的度数; ②延长BO交⊙O于点A,连结AC,求∠C的度数。80°40°1.圆心角的定义?顶点在圆心的角叫圆心角.2.圆心角、弧、弦三个量之间关系在同圆或等圆中,如果圆心角、弧、弦有 一组量相等,那么它们所对应的其余两个 量都分别相等。动脑筋圆心角的顶点发生变化时,我们得到几种情况:圆周角回忆你能仿照圆心角的定义给圆周角下个定义吗? 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征:① 角的顶点在圆上.② 角的两边都与圆相交.不是不是不是不是是圆周角性质定理:1、画一个圆心角,然后再画同弧所对的圆周角. 2、一条弧所对的圆周角有多少个?圆心角呢?一条弧所对的圆周角有无数个。
圆心角只有一个。圆周角与同弧所对的圆心角有什么关系?结论:一条弧所对的圆周角等于它所对的圆心角的一半.圆周角的度数就等于所对弧度数的一半。1、如图,圆心角∠AOB=100°,则∠ACB=______。2、 如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________3、在圆O中,一条弧所对的圆心角和圆周角分别为(2x+100)0和(5x-30)0,则这条弧的度数为____4、如图,已知∠ACB=20°,
则∠AOB= ,∠OAB= 。 40° 70°130°25° 140°5.如图:OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.∠AOC=2∠BOC∠ACB=2∠BAC证明:∠ACB= 0.5∠AOB6、已知,⊙O的弦AB长等于圆的半径,求该弦所对的圆心角和圆周角的度数。∠AOB=60°∠ACB=30°∠ADB=150°7、如图,在⊙O中,AB是直径,半径CO⊥AB, D是CO的中点,DE // AB,求∠ABE的度数.∠ABE=15°8、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,求∠BOC的度数。∠A=21°∠BOC=140°1、圆周角的定义。 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征:① 角的顶点在圆上.② 角的两边都与圆相交.2、圆周角定理及其定理应用。一条弧所对的圆周角等于它所对的圆心角的一半.方法上主要学习了圆周角定理的证明,渗透了 “特殊到一般”的思想方法和分类讨论的思想方法。圆周角(2)1、圆周角的定义。 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征:① 角的顶点在圆上.② 角的两边都与圆相交.2、圆周角定理及其定理应用。一条弧所对的圆周角等于它所对的圆心角的一半.1.如图,在⊙O中,∠BAC=32o,则∠BOC=________。64o130o2、如图,⊙O中,∠ACB = 115o,
则∠AOB=______。问题1、如图,在⊙O中,∠B、∠D、∠E的
大小有什么关系?为什么?∠B=∠D=∠E同圆或等圆中,同弧或等弧所对的圆周角相等; 反之,相等的圆周角所对的弧也相等。问题2、如图,BC是⊙O的直径,A是⊙O上任一点,
你能确定∠BAC的度数吗?∠BOC=180o问题3、如图,圆周角∠BAC =90o,
弦BC经过圆心O吗?为什么?直径(或半圆)所对的圆周角是直角;
90°的圆周角所对的弦是直径。1、如图,点A、B、C、D在同一个圆上,四边形的对角线把4个内角分成8个角,这些角中哪些是相等的角? ∠2=∠7∠1=∠4∠3=∠6∠5=∠82、如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.∵AB是直径,∴ ∠ACB= ∠ADB=90°在Rt△ABC中,由勾股定理BC=8cm∵CD平分∠ACB,∠ACD= ∠BCD3.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下. 4、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A.∠BAC=∠BDC∠DAC=∠DBC∠A=∠BAC+∠DAC
=∠BDC+∠DBC
=20°+30°=50°证明:连结AD.∵AB是圆的直径∴∠ADB=90°,∴AD⊥BC∵AB=AC,∴AD平分∠BAC,即∠BAD=∠CAD, 课外练习 1、如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于E、F,比较∠BAC与∠BDC的大小,
并说明理由。连结CF,∠BFC是△CDF的一个外角。∴∠BFC>∠BDC,又∠BAC=∠BFC∴∠BAC>∠BDC,也可连结FC,证法相同2、如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?(1)AE = BE,AC = BC,AD = BD(2)AC = BC,∠CAB = ∠ABC = ∠ADC,
∠ACE =∠BCE =∠DAB(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE一、知识点:顶点在圆上两边都和圆相交二、体现的数学思想:由特殊到一般和分类讨论的思想。三、方法思考:
1、证明题的思路寻找方法; 2、等积式的证明方法; 3、添辅助线的方法。
数学 九年级下册 湘教版
第2章 圆
2.2 圆心角、圆周角圆心角1、圆的概念是什么?2、圆的对称性:圆上任意两点间的部分叫作圆弧,简称弧.如图圆O上两点A,B间的小于半圆的部分
叫作劣弧,用符号“⌒”表示.A,B间的大于半圆的部分叫作优弧,圆是中心对称图形,圆心是它的对称中心。·O如图,∠AOB是怎样构成的?两条半径所形成的角叫圆心角。 在生活中,我们常遇到圆心角,
如飞靶中有圆心角,还有手表中的
时针与分针所成的角也是圆心角.下面所示的角,哪个是圆心角?概念学习圆心角、弦、弧的关系1、实验操作:在两张透明的纸上,分别作半径相等的⊙O和⊙O',
在⊙O和⊙O'中,作圆心角∠AOB和∠A'O'B',
连接AB和A'B',将两张纸重叠,
使⊙O和⊙O'重合。当∠AOB=∠A'O'B'时,弦AB A'B',2、探究思考:==3、在同一圆中,∠AOB=∠COD
由旋转不变性得:AB=CD,∠AOB=∠COD结论:在同圆或等圆中,如果圆心角相等,
那么它们所对的弧相等,所对的弦也相等.·OCBDA议一议 在同圆或等圆中,如果弦相等,那么它们所对的圆心角相等吗?所对的弧相等吗?你能讲出道理吗? 在同圆或等圆中,如果弧相等,那么它们所对的圆心角相等吗?所对的弦也相等吗?你能讲出道理吗?∠AOB=∠CODAB=CD∠AOB=∠CODAB=CD在同圆或等圆中,
如果两个圆心角,两条弧,两条弦中有一组量相等,
那么它们所对应的其余各组都分别相等。no的圆心角对着no的弧,
no的弧对着no的圆心角。圆心角的度数与它所对弧的度数相等。小知识2、已知⊙O的半径是5 cm,弦AB长是5 cm,则圆心角∠AOB= .60o35o解:连结CD,∠A=90o-28o=62o∠ACD=180o-62o×2=56o∠ECD=34o提示:证明?AOD、?DOC、?COB是
等边三角形,∠DCB=120o∠EOB=40o,∠AOC=∠COE=∠DOB=70o∠AOD=110o6、如图,已知CD是⊙O直径,圆心角∠AOB=30o,
弦CA//OB,求∠BOD的度数。7、如图,AB是⊙O直径,AC=CD,∠COD=60o,
(1)求证:?AOC是等边三角形。
(2)求证:OC//BD由CA//OB,∠AOB=30o,
得∠CAO=∠ACO=30o ∴∠AOC=120o∴∠AOD=60o∴∠BOD=30o(1)仿第4题得证(2)?AOC≌?BOD∴∠AOC=∠DBO=60o∴OC//BD1.圆是中心对称图形,圆心是它的对称中心。2.在同圆或等圆中,
如果两个圆心角,两条弧,两条弦中有一组量相等,
那么它们所对应的其余各组都分别相等。3.圆心角的度数与它所对弧的度数相等。练 习 巩 固:练习第1、2题作 业 布 置:
习题2.2第1、2题圆周角(1)3、如图,已知∠BOC=80°, ①求AB弧的度数; ②延长BO交⊙O于点A,连结AC,求∠C的度数。80°40°1.圆心角的定义?顶点在圆心的角叫圆心角.2.圆心角、弧、弦三个量之间关系在同圆或等圆中,如果圆心角、弧、弦有 一组量相等,那么它们所对应的其余两个 量都分别相等。动脑筋圆心角的顶点发生变化时,我们得到几种情况:圆周角回忆你能仿照圆心角的定义给圆周角下个定义吗? 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征:① 角的顶点在圆上.② 角的两边都与圆相交.不是不是不是不是是圆周角性质定理:1、画一个圆心角,然后再画同弧所对的圆周角. 2、一条弧所对的圆周角有多少个?圆心角呢?一条弧所对的圆周角有无数个。
圆心角只有一个。圆周角与同弧所对的圆心角有什么关系?结论:一条弧所对的圆周角等于它所对的圆心角的一半.圆周角的度数就等于所对弧度数的一半。1、如图,圆心角∠AOB=100°,则∠ACB=______。2、 如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________3、在圆O中,一条弧所对的圆心角和圆周角分别为(2x+100)0和(5x-30)0,则这条弧的度数为____4、如图,已知∠ACB=20°,
则∠AOB= ,∠OAB= 。 40° 70°130°25° 140°5.如图:OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.∠AOC=2∠BOC∠ACB=2∠BAC证明:∠ACB= 0.5∠AOB6、已知,⊙O的弦AB长等于圆的半径,求该弦所对的圆心角和圆周角的度数。∠AOB=60°∠ACB=30°∠ADB=150°7、如图,在⊙O中,AB是直径,半径CO⊥AB, D是CO的中点,DE // AB,求∠ABE的度数.∠ABE=15°8、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,求∠BOC的度数。∠A=21°∠BOC=140°1、圆周角的定义。 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征:① 角的顶点在圆上.② 角的两边都与圆相交.2、圆周角定理及其定理应用。一条弧所对的圆周角等于它所对的圆心角的一半.方法上主要学习了圆周角定理的证明,渗透了 “特殊到一般”的思想方法和分类讨论的思想方法。圆周角(2)1、圆周角的定义。 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征:① 角的顶点在圆上.② 角的两边都与圆相交.2、圆周角定理及其定理应用。一条弧所对的圆周角等于它所对的圆心角的一半.1.如图,在⊙O中,∠BAC=32o,则∠BOC=________。64o130o2、如图,⊙O中,∠ACB = 115o,
则∠AOB=______。问题1、如图,在⊙O中,∠B、∠D、∠E的
大小有什么关系?为什么?∠B=∠D=∠E同圆或等圆中,同弧或等弧所对的圆周角相等; 反之,相等的圆周角所对的弧也相等。问题2、如图,BC是⊙O的直径,A是⊙O上任一点,
你能确定∠BAC的度数吗?∠BOC=180o问题3、如图,圆周角∠BAC =90o,
弦BC经过圆心O吗?为什么?直径(或半圆)所对的圆周角是直角;
90°的圆周角所对的弦是直径。1、如图,点A、B、C、D在同一个圆上,四边形的对角线把4个内角分成8个角,这些角中哪些是相等的角? ∠2=∠7∠1=∠4∠3=∠6∠5=∠82、如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.∵AB是直径,∴ ∠ACB= ∠ADB=90°在Rt△ABC中,由勾股定理BC=8cm∵CD平分∠ACB,∠ACD= ∠BCD3.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下. 4、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A.∠BAC=∠BDC∠DAC=∠DBC∠A=∠BAC+∠DAC
=∠BDC+∠DBC
=20°+30°=50°证明:连结AD.∵AB是圆的直径∴∠ADB=90°,∴AD⊥BC∵AB=AC,∴AD平分∠BAC,即∠BAD=∠CAD, 课外练习 1、如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于E、F,比较∠BAC与∠BDC的大小,
并说明理由。连结CF,∠BFC是△CDF的一个外角。∴∠BFC>∠BDC,又∠BAC=∠BFC∴∠BAC>∠BDC,也可连结FC,证法相同2、如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?(1)AE = BE,AC = BC,AD = BD(2)AC = BC,∠CAB = ∠ABC = ∠ADC,
∠ACE =∠BCE =∠DAB(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE一、知识点:顶点在圆上两边都和圆相交二、体现的数学思想:由特殊到一般和分类讨论的思想。三、方法思考:
1、证明题的思路寻找方法; 2、等积式的证明方法; 3、添辅助线的方法。
