人教A版高中数学 选修4-1 第二讲 五 与圆相关的比例线段 上课课件(共30张PPT)
文档属性
| 名称 | 人教A版高中数学 选修4-1 第二讲 五 与圆相关的比例线段 上课课件(共30张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 415.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 20:38:41 | ||
图片预览






文档简介
(共30张PPT)
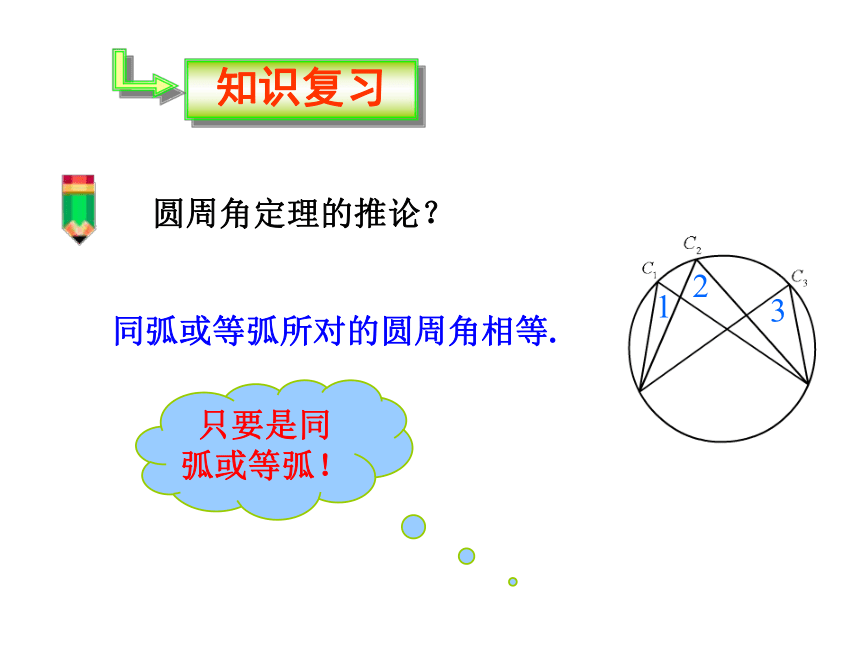
旧知回顾
圆周角定理?
圆上一条弧所对的圆周角等于它所对的圆心角的一半 .
A
B
C
O
1
2
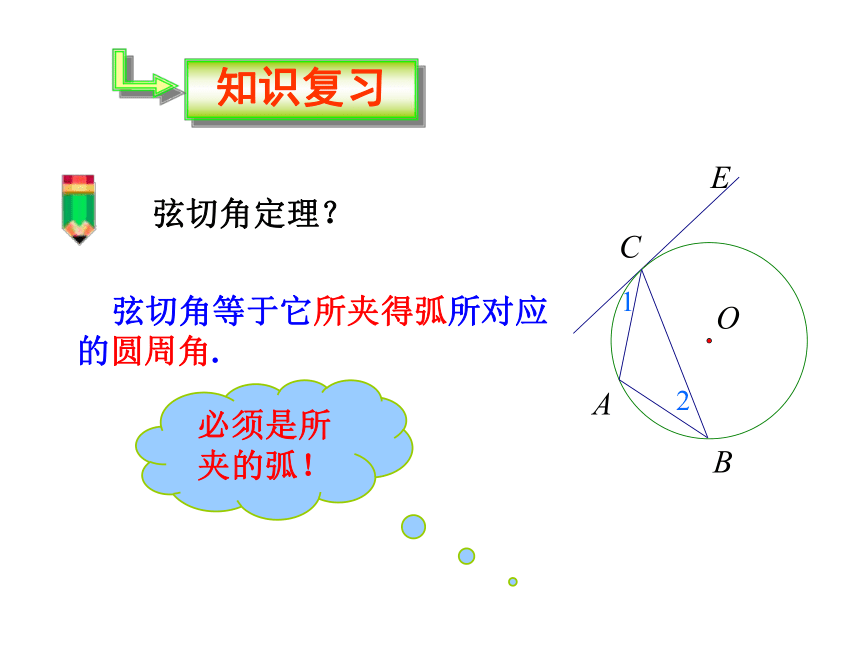
圆周角定理的推论?
同弧或等弧所对的圆周角相等.
知识复习
只要是同弧或等弧!
1
2
3
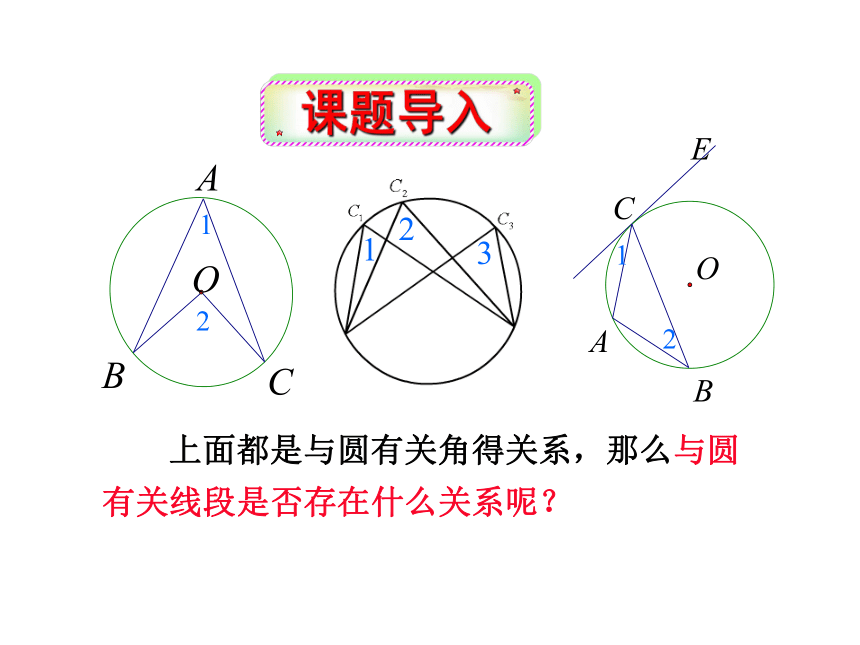
弦切角定理?
弦切角等于它所夹得弧所对应的圆周角.
知识复习
必须是所夹的弧!
E
O
C
A
B
1
2
上面都是与圆有关角得关系,那么与圆有关线段是否存在什么关系呢?
课题导入
A
B
C
O
1
2
1
2
3
E
O
C
A
B
1
2
探究
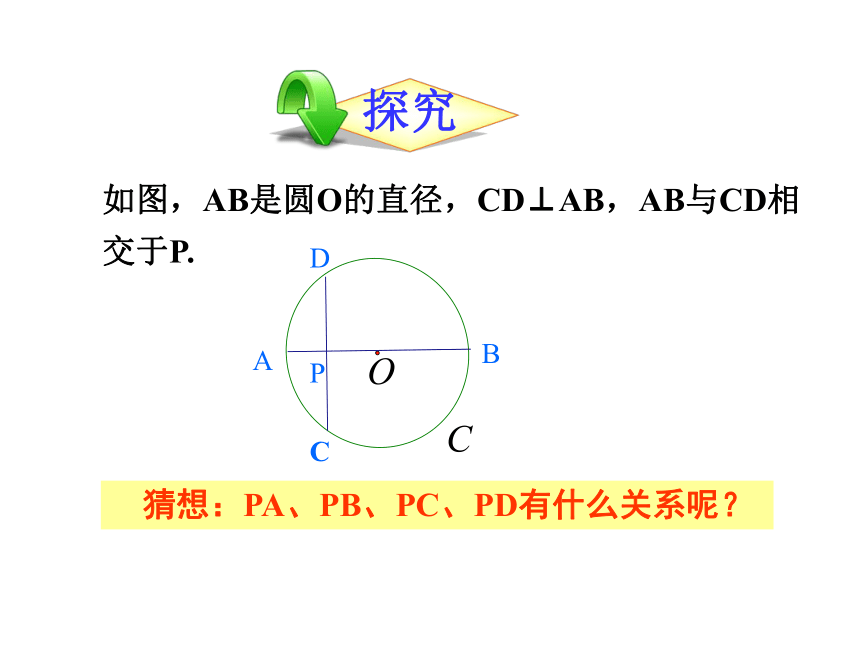
如图,AB是圆O的直径,CD⊥AB,AB与CD相交于P.
猜想:PA、PB、PC、PD有什么关系呢?
B
A
C
O
C
D
P
2.5 与圆相关的比例线段
教学目标
理解和掌握相交弦定理、割线定理、切割线定理、切线长定理,并能够应用定理解决和证明相关的几何问题.
知识与能力
过程与方法
通过经历相交弦定理、割线定理、切割线定理、切线长定理的探究过程,体会和掌握运动变化数学思想,并能认识四条定理的内在联系,培养学生的发散思维和严谨的逻辑思维.
情感态度与价值观
提高学生学习数学的积极性,培养他们勤于思考,敢于探索的思维习惯,使学生体会到数学的逻辑严谨的特征.
教学重难点
重点
难点
掌握相交弦定理、割线定理、切割线定理、切线长定理.
相交弦定理、割线定理、切割线定理、切线长定理的探究过程及其在几何中应用.
C
D
B
O
A
P
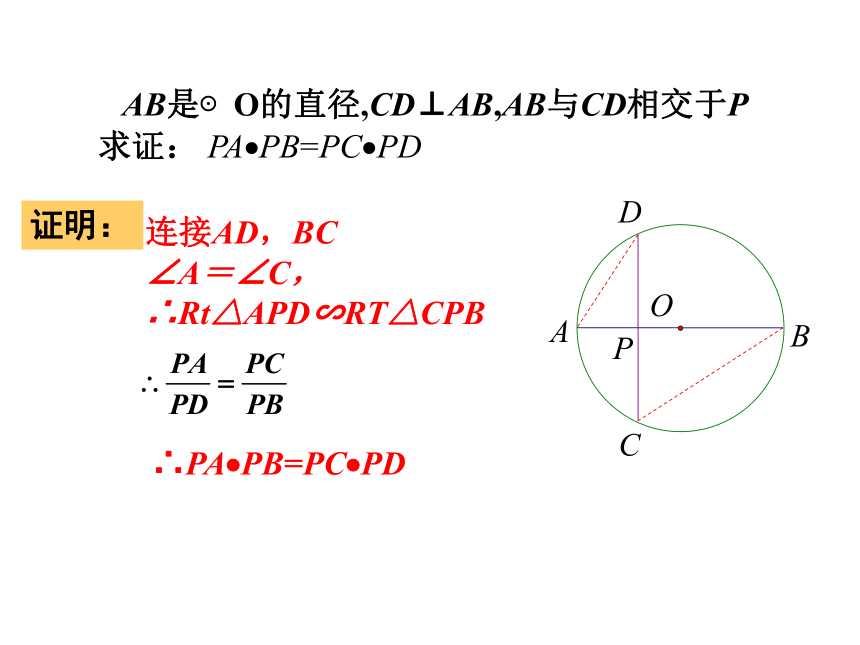
AB是⊙O的直径,CD⊥AB,AB与CD相交于P
求证: PA?PB=PC?PD
连接AD,BC
∠A=∠C,
∴Rt△APD∽RT△CPB
∴PA?PB=PC?PD
证明:
探究
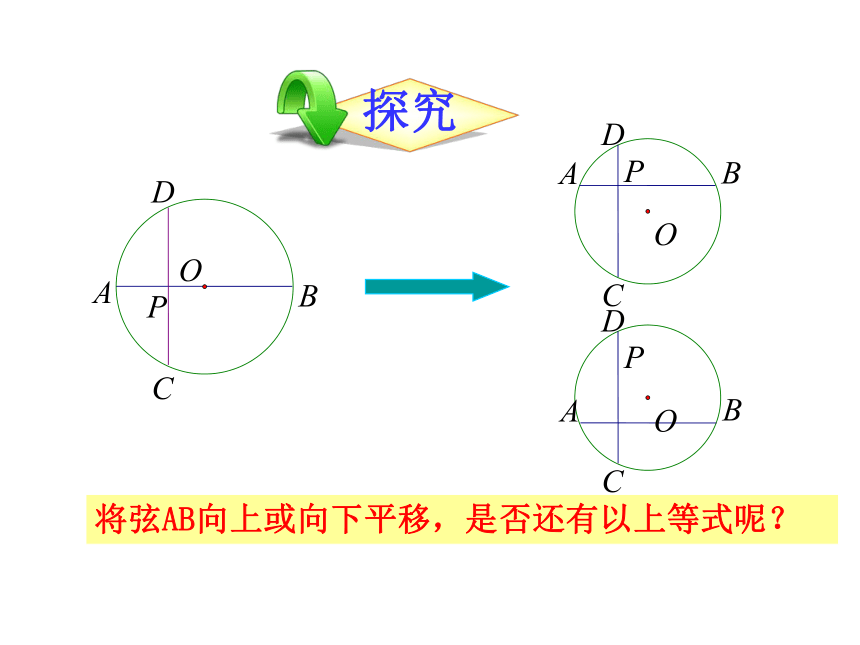
将弦AB向上或向下平移,是否还有以上等式呢?
C
D
B
O
A
P
C
D
O
A
B
P
C
D
O
A
B
P
C
D
O
A
B
P
△APD∽△CPB
PA?PB=PC?PD
C
D
O
A
B
P
连接AD,BC
∠A=∠C,
∴Rt△APD∽Rt△CPB
证明:
知识要点
相交弦定理:
圆内的两条相交弦,被交点分成的两条线段长的积相等.
如图,圆内的两条弦AB、CD相交于圆内一点P,已知PA=PB=4,PC=?PD.求CD长.
P
O
A
B
C
D
解:
设CD=x,则PD=?x,PC=x
PA?PB=PC?PD
4×4=?x??x
x=10
∴CD=10.
小练习
P
O
A
B
D
C
PA?PB=PC?PD
D
(C,P)A
B
O
A
C
D
P
B
O
?
D
(C,P)A
B
O
A
C
D
P
B
O
PA=PC=0
易得△PAD∽△PCB
PA?PB=PC?PD
PA?PB=PC?PD
连接AD、BC
知识要点
割线定理:
从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等 .
A
C
D
P
B
O
C
A(B)
O
P
D
PA?PA(B)=PC?PD
?
探究
D
A(B)
O
P
C
∴△PAC∽△PDA
PA2=PC?PD
证明:
连接AD,BC
∠PBD=∠C,
∠P是公共角,
继续解答……
知识要点
切割线定理:
从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项 .
PA?PA(B)=PC?PC(D)
?
探究
D
A(B)
O
P
C
C(D)
A(B)
O
P
∴△PAC≌△PDA
OP是∠CPA的角平分线.
证明:
连接PA,PC,PO
∵OC⊥PC,OA⊥PA,
OA=OC,OP=OP,
继续解答……
C(D)
A(B)
O
P
知识要点
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
课堂小结
圆内的两条相交弦,被交点分成的两条线段长的积相等.
1、相交弦定理
从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.
2、割线定理
从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
3、切割线定理
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
4、切线长定理
1、从圆外一点P向圆引两条割线PAB、PCD,分别与圆相交于A、B、C、D,如果PA=4,PC=3,CD=5,那么AB ( )
A.4 B. 3 C. 2 D. 1
C
由割线定理 ,PA·PB=PC·PD
∴ 4*PB=3*(3+5)
∴PB=6,AB=PB-PA=2.
课堂练习
解析
A
C
D
P
B
O
2、如图,AB为⊙O直径,弦CD垂直AB于P,CP=4,AP=2,则PO 等于( )
A.4 B. 3 C. 2 D. 1
B
由相交弦定理 ,PA·PB=PC·PD
∵PC=PD,∴ 2*PB=4*4
∴PB=8,AB=PB+PA=10.
∴PO=5-2=3.
解析
C
D
B
O
A
P
3、如图,PAB为⊙O的割线,PC切⊙O于C,PC=10,AB=15,则PA长 ( )
A.5 B. 6 C. 7 D. 8
A
由切割线定理 ,PC2=PA·PB
∴ 10*10=PA*(PA+15)
∴PA=5.
解析
A
C
O
P
B
4.如图AB是⊙O的直径,过A、B引两条弦AD和BE,相交于点C.
求证: AC?AD+BC?BE=AB2
B
F
C
A
D
E
证明: 连接AE、BD,过点C作CF⊥AB,与AB交于F
∵AB是圆的直径,
∴∠AEB=∠ADB=90?
∵∠AFC=90?
∴A、F、C、E四点共圆
∴BC?BE=BF?BA
同理 F、B、D、C四点共圆
∴AC?AD=AF?AB
∴AC?AD+BC?BE=AB(AF+BF)=AB2
旧知回顾
圆周角定理?
圆上一条弧所对的圆周角等于它所对的圆心角的一半 .
A
B
C
O
1
2
圆周角定理的推论?
同弧或等弧所对的圆周角相等.
知识复习
只要是同弧或等弧!
1
2
3
弦切角定理?
弦切角等于它所夹得弧所对应的圆周角.
知识复习
必须是所夹的弧!
E
O
C
A
B
1
2
上面都是与圆有关角得关系,那么与圆有关线段是否存在什么关系呢?
课题导入
A
B
C
O
1
2
1
2
3
E
O
C
A
B
1
2
探究
如图,AB是圆O的直径,CD⊥AB,AB与CD相交于P.
猜想:PA、PB、PC、PD有什么关系呢?
B
A
C
O
C
D
P
2.5 与圆相关的比例线段
教学目标
理解和掌握相交弦定理、割线定理、切割线定理、切线长定理,并能够应用定理解决和证明相关的几何问题.
知识与能力
过程与方法
通过经历相交弦定理、割线定理、切割线定理、切线长定理的探究过程,体会和掌握运动变化数学思想,并能认识四条定理的内在联系,培养学生的发散思维和严谨的逻辑思维.
情感态度与价值观
提高学生学习数学的积极性,培养他们勤于思考,敢于探索的思维习惯,使学生体会到数学的逻辑严谨的特征.
教学重难点
重点
难点
掌握相交弦定理、割线定理、切割线定理、切线长定理.
相交弦定理、割线定理、切割线定理、切线长定理的探究过程及其在几何中应用.
C
D
B
O
A
P
AB是⊙O的直径,CD⊥AB,AB与CD相交于P
求证: PA?PB=PC?PD
连接AD,BC
∠A=∠C,
∴Rt△APD∽RT△CPB
∴PA?PB=PC?PD
证明:
探究
将弦AB向上或向下平移,是否还有以上等式呢?
C
D
B
O
A
P
C
D
O
A
B
P
C
D
O
A
B
P
C
D
O
A
B
P
△APD∽△CPB
PA?PB=PC?PD
C
D
O
A
B
P
连接AD,BC
∠A=∠C,
∴Rt△APD∽Rt△CPB
证明:
知识要点
相交弦定理:
圆内的两条相交弦,被交点分成的两条线段长的积相等.
如图,圆内的两条弦AB、CD相交于圆内一点P,已知PA=PB=4,PC=?PD.求CD长.
P
O
A
B
C
D
解:
设CD=x,则PD=?x,PC=x
PA?PB=PC?PD
4×4=?x??x
x=10
∴CD=10.
小练习
P
O
A
B
D
C
PA?PB=PC?PD
D
(C,P)A
B
O
A
C
D
P
B
O
?
D
(C,P)A
B
O
A
C
D
P
B
O
PA=PC=0
易得△PAD∽△PCB
PA?PB=PC?PD
PA?PB=PC?PD
连接AD、BC
知识要点
割线定理:
从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等 .
A
C
D
P
B
O
C
A(B)
O
P
D
PA?PA(B)=PC?PD
?
探究
D
A(B)
O
P
C
∴△PAC∽△PDA
PA2=PC?PD
证明:
连接AD,BC
∠PBD=∠C,
∠P是公共角,
继续解答……
知识要点
切割线定理:
从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项 .
PA?PA(B)=PC?PC(D)
?
探究
D
A(B)
O
P
C
C(D)
A(B)
O
P
∴△PAC≌△PDA
OP是∠CPA的角平分线.
证明:
连接PA,PC,PO
∵OC⊥PC,OA⊥PA,
OA=OC,OP=OP,
继续解答……
C(D)
A(B)
O
P
知识要点
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
课堂小结
圆内的两条相交弦,被交点分成的两条线段长的积相等.
1、相交弦定理
从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.
2、割线定理
从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
3、切割线定理
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
4、切线长定理
1、从圆外一点P向圆引两条割线PAB、PCD,分别与圆相交于A、B、C、D,如果PA=4,PC=3,CD=5,那么AB ( )
A.4 B. 3 C. 2 D. 1
C
由割线定理 ,PA·PB=PC·PD
∴ 4*PB=3*(3+5)
∴PB=6,AB=PB-PA=2.
课堂练习
解析
A
C
D
P
B
O
2、如图,AB为⊙O直径,弦CD垂直AB于P,CP=4,AP=2,则PO 等于( )
A.4 B. 3 C. 2 D. 1
B
由相交弦定理 ,PA·PB=PC·PD
∵PC=PD,∴ 2*PB=4*4
∴PB=8,AB=PB+PA=10.
∴PO=5-2=3.
解析
C
D
B
O
A
P
3、如图,PAB为⊙O的割线,PC切⊙O于C,PC=10,AB=15,则PA长 ( )
A.5 B. 6 C. 7 D. 8
A
由切割线定理 ,PC2=PA·PB
∴ 10*10=PA*(PA+15)
∴PA=5.
解析
A
C
O
P
B
4.如图AB是⊙O的直径,过A、B引两条弦AD和BE,相交于点C.
求证: AC?AD+BC?BE=AB2
B
F
C
A
D
E
证明: 连接AE、BD,过点C作CF⊥AB,与AB交于F
∵AB是圆的直径,
∴∠AEB=∠ADB=90?
∵∠AFC=90?
∴A、F、C、E四点共圆
∴BC?BE=BF?BA
同理 F、B、D、C四点共圆
∴AC?AD=AF?AB
∴AC?AD+BC?BE=AB(AF+BF)=AB2
