人教A版高中数学 选修4-1 第二讲 一 圆周角定理 上课课件(共30张PPT)
文档属性
| 名称 | 人教A版高中数学 选修4-1 第二讲 一 圆周角定理 上课课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 554.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 20:39:41 | ||
图片预览









文档简介
(共30张PPT)
旧知回顾
顶点在圆心的角叫圆心角.顶点在圆周上,两边和圆相交的角叫做圆周角.
.O
A
B
C
圆心角和圆周角是如何定义的?
半圆或直径所对的圆周角等于多少度?
课题导入
半圆或直径所对的圆周角都等于90°(直角).
反过来也是成立吗?
结论
探究
圆周角和圆心角之间有的关系?
.O
A
B
C
思考?
2.1 圆周角定理
教学目标
理解和掌握圆周角定理以及两个相关的推论,并能够用这个定理和推论解决有关的几何问题.
知识与能力
过程与方法
学习并领会圆周角定理的证明推导过程,应用圆周角定理解决几何问题过程,使学生体会和掌握“分类”和“转化”这两种数学思想在几何证明中的作用,培养学生的发散思维和严谨的逻辑思维.
情感态度与价值观
提高学生学习数学的积极性,培养他们勤于思考,敢于探索的思维习惯,使学生体会到数学的逻辑严谨的特征.
教学重难点
重点
难点
掌握圆周角定理,圆心角定理及其圆周角的两个推论.
圆周角定理,圆心角定理的证明及其应用.
圆周角和圆心角的关系
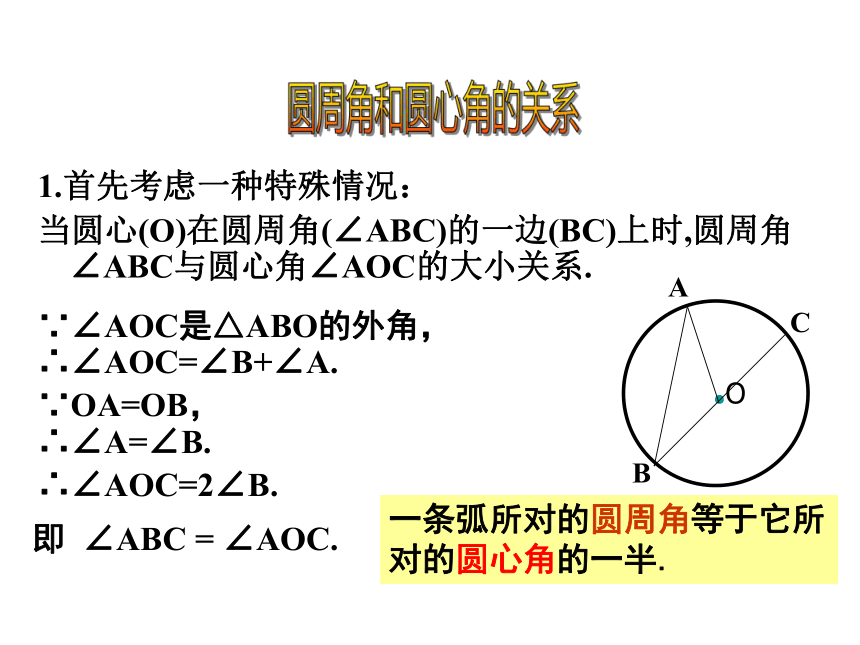
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
●O
A
B
C
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角和圆心角的关系
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
思考:能否转化为1的情况?
过点B作直径BD.由1可得:
●O
∴ ∠ABC = 1/2∠AOC.
A
B
C
∠ABD = 1/2∠AOD,∠CBD = 1/2∠COD,
D
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角和圆心角的关系
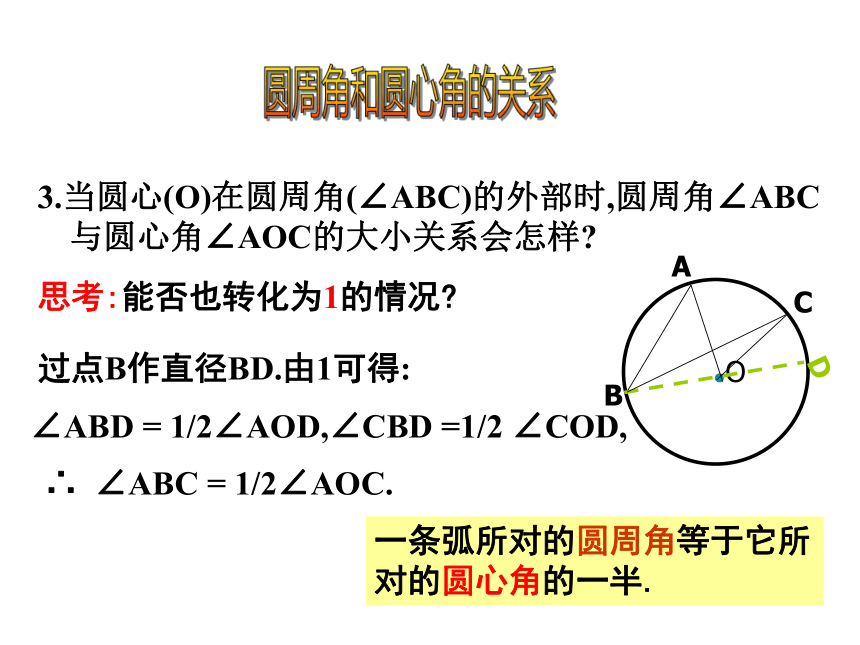
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
思考:能否也转化为1的情况?
过点B作直径BD.由1可得:
●O
∴ ∠ABC = 1/2∠AOC.
D
∠ABD = 1/2∠AOD,∠CBD =1/2 ∠COD,
A
B
C
一条弧所对的圆周角等于它所对的圆心角的一半.
知识要点
圆周角定理:
圆上一条弧所对的圆周角等于它所对的圆心角的一半 .
小练习
1、⊙O的半径为5,圆心的坐标为(0,0)点P的坐标为(4,2),点A的坐标为(4,-3),则点P与⊙O的位置关系是 ,点A在⊙O的 .
2、一个点与定圆上最近的距离为4㎝,最远点的距离为9㎝,则此圆的半径为 .
A(4,-3)
x
y
o
.
.
P
(4,2)
1题
5
3
4
2
4
5
2
.
.
O
P
4㎝
9㎝
A
B
2题
回顾
我们知道,一个周角是360°.把圆周等分成360份,每份叫做1°的弧.
由此,n°的圆心角所对的弧是n°的弧;反之,n°的弧所对的圆心角的度数是n°.从而有:
知识要点
圆心角定理:
圆心角的度数等于它所对弧的度数 .
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?
实际问题数学化
B
A
C
D
E
●O
B
A
C
D
E
B,D,E为球员,AC为球门,分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?
在同圆内,同弧或等弧所对的圆周角相等.
知识要点
圆周角定理的推论1:
同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
小练习
如图,△ABC内接于圆,D是弧BC的中点,AD交BC于E,
求证:AB·AC=AE·AD
△ABD∽ △AEC
分析:要证AB · AC = AE · AD
∠1=∠2
∠C=∠D
AC
AD
AE
AB
=
探究
90°的圆周角所对的弦是直径?
思 考
知识要点
圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
小练习
如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D.已知CD=2cm,AD=1cm,求AB的长.
O
A
B
C
D
r
r-1
2
解一
解二
连接CO,利用勾股定理
求出半径:r2=(r-1)2+22
连接CA,CB利用射影定理
求出DB
课堂小结
2、圆心角定理
圆上一条弧所对的圆周角等于它所对的圆心角的一半.
1、圆周角定理
圆心角的度数等于它所对弧的度数.
2、圆周角定理的推论
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
1、如图,AB为⊙O的直径,C为⊙O上的一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于P,则当C在⊙O上运动时,点P的位置( )
A.随点C的运动而变化
B.不变
C.在使PA=OA的劣弧上
D.无法判断
1
2
3
4
5
B
∠1=∠2= ∠3
∠4=∠5
∠CDO=∠POD=90°
课堂练习
解析
2、如图,在⊙O中,弦AB、CD垂直相交于点E,求证:∠BOC+∠AOD=180°.
1
3
2
∠BOC+∠AOD=∠1+∠3
=2∠2+2∠ABD
=2(∠2+∠ABD)
=2 ×90°
=180°
解:
3、已知:△ABC为⊙O的内接三角形,⊙O的直径BD交AC于E.AF⊥BD于F,延长AF交BC于G,
求证:AB2=BG·BC.
分析:要证AB2=BG·BC
△ABG∽ △CBA
1
∠ABG =∠CBA
∠1= ∠C
连接BH,利用等孤所对的圆周角相等:
2
∠1= ∠2=∠C
即证.
4、如图,以△ABC的BC边为直径的半圆交AB于D,交AC于E,过E作EF⊥BC,垂足为F,且BF:FC=5:1,AB=8,AE=2,求EC的长.
分析:连接BE,得AC BE
则BE2=AB2-AE2=60
由射影定理可知BE2=BF·BC
即 5/6BC2=60
BC2=72
CE2=BC2-BE2=12.
旧知回顾
顶点在圆心的角叫圆心角.顶点在圆周上,两边和圆相交的角叫做圆周角.
.O
A
B
C
圆心角和圆周角是如何定义的?
半圆或直径所对的圆周角等于多少度?
课题导入
半圆或直径所对的圆周角都等于90°(直角).
反过来也是成立吗?
结论
探究
圆周角和圆心角之间有的关系?
.O
A
B
C
思考?
2.1 圆周角定理
教学目标
理解和掌握圆周角定理以及两个相关的推论,并能够用这个定理和推论解决有关的几何问题.
知识与能力
过程与方法
学习并领会圆周角定理的证明推导过程,应用圆周角定理解决几何问题过程,使学生体会和掌握“分类”和“转化”这两种数学思想在几何证明中的作用,培养学生的发散思维和严谨的逻辑思维.
情感态度与价值观
提高学生学习数学的积极性,培养他们勤于思考,敢于探索的思维习惯,使学生体会到数学的逻辑严谨的特征.
教学重难点
重点
难点
掌握圆周角定理,圆心角定理及其圆周角的两个推论.
圆周角定理,圆心角定理的证明及其应用.
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
●O
A
B
C
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角和圆心角的关系
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
思考:能否转化为1的情况?
过点B作直径BD.由1可得:
●O
∴ ∠ABC = 1/2∠AOC.
A
B
C
∠ABD = 1/2∠AOD,∠CBD = 1/2∠COD,
D
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角和圆心角的关系
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
思考:能否也转化为1的情况?
过点B作直径BD.由1可得:
●O
∴ ∠ABC = 1/2∠AOC.
D
∠ABD = 1/2∠AOD,∠CBD =1/2 ∠COD,
A
B
C
一条弧所对的圆周角等于它所对的圆心角的一半.
知识要点
圆周角定理:
圆上一条弧所对的圆周角等于它所对的圆心角的一半 .
小练习
1、⊙O的半径为5,圆心的坐标为(0,0)点P的坐标为(4,2),点A的坐标为(4,-3),则点P与⊙O的位置关系是 ,点A在⊙O的 .
2、一个点与定圆上最近的距离为4㎝,最远点的距离为9㎝,则此圆的半径为 .
A(4,-3)
x
y
o
.
.
P
(4,2)
1题
5
3
4
2
4
5
2
.
.
O
P
4㎝
9㎝
A
B
2题
回顾
我们知道,一个周角是360°.把圆周等分成360份,每份叫做1°的弧.
由此,n°的圆心角所对的弧是n°的弧;反之,n°的弧所对的圆心角的度数是n°.从而有:
知识要点
圆心角定理:
圆心角的度数等于它所对弧的度数 .
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?
实际问题数学化
B
A
C
D
E
●O
B
A
C
D
E
B,D,E为球员,AC为球门,分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?
在同圆内,同弧或等弧所对的圆周角相等.
知识要点
圆周角定理的推论1:
同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
小练习
如图,△ABC内接于圆,D是弧BC的中点,AD交BC于E,
求证:AB·AC=AE·AD
△ABD∽ △AEC
分析:要证AB · AC = AE · AD
∠1=∠2
∠C=∠D
AC
AD
AE
AB
=
探究
90°的圆周角所对的弦是直径?
思 考
知识要点
圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
小练习
如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D.已知CD=2cm,AD=1cm,求AB的长.
O
A
B
C
D
r
r-1
2
解一
解二
连接CO,利用勾股定理
求出半径:r2=(r-1)2+22
连接CA,CB利用射影定理
求出DB
课堂小结
2、圆心角定理
圆上一条弧所对的圆周角等于它所对的圆心角的一半.
1、圆周角定理
圆心角的度数等于它所对弧的度数.
2、圆周角定理的推论
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
1、如图,AB为⊙O的直径,C为⊙O上的一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于P,则当C在⊙O上运动时,点P的位置( )
A.随点C的运动而变化
B.不变
C.在使PA=OA的劣弧上
D.无法判断
1
2
3
4
5
B
∠1=∠2= ∠3
∠4=∠5
∠CDO=∠POD=90°
课堂练习
解析
2、如图,在⊙O中,弦AB、CD垂直相交于点E,求证:∠BOC+∠AOD=180°.
1
3
2
∠BOC+∠AOD=∠1+∠3
=2∠2+2∠ABD
=2(∠2+∠ABD)
=2 ×90°
=180°
解:
3、已知:△ABC为⊙O的内接三角形,⊙O的直径BD交AC于E.AF⊥BD于F,延长AF交BC于G,
求证:AB2=BG·BC.
分析:要证AB2=BG·BC
△ABG∽ △CBA
1
∠ABG =∠CBA
∠1= ∠C
连接BH,利用等孤所对的圆周角相等:
2
∠1= ∠2=∠C
即证.
4、如图,以△ABC的BC边为直径的半圆交AB于D,交AC于E,过E作EF⊥BC,垂足为F,且BF:FC=5:1,AB=8,AE=2,求EC的长.
分析:连接BE,得AC BE
则BE2=AB2-AE2=60
由射影定理可知BE2=BF·BC
即 5/6BC2=60
BC2=72
CE2=BC2-BE2=12.
