人教A版高中数学 选修4-1 第三讲 三 平面与圆锥面的截线 上课课件(共27张PPT)
文档属性
| 名称 | 人教A版高中数学 选修4-1 第三讲 三 平面与圆锥面的截线 上课课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 20:40:35 | ||
图片预览







文档简介
(共27张PPT)
新课导入
Dandelin(1794-1847) 丹德林,比利时人. 出生于巴黎附近的布尔日,曾在列日、纳缪尔和柳基赫等地工作.他是比利时科学院院士.丹德林主要研究代数和几何.
Dandelin(1794-1847)
事迹 :
1. 在代数方面,他于1826年提出了一种求方程根的近似方法,与罗巴切夫斯基、格雷菲提出的方法相似.
2. 在几何方面,他于1822年证明了关于圆锥曲线与圆锥的关系的一个十分有趣的定理,后来,这个球面被称为丹德林球面.
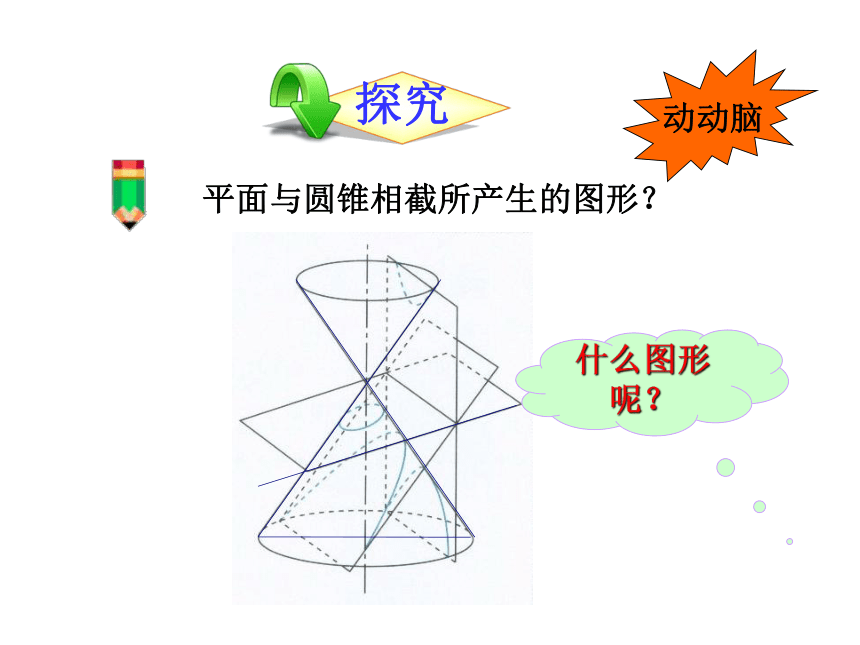
平面与圆锥相截所产生的图形?
探究
动动脑
什么图形呢?
3.3 平面与圆锥面的截线
教学目标
探究定理2的证明并掌握其定理,理解圆锥曲线的结构特点.
知识与能力
过程与方法
通过探究定理2的证明过程,感知Dandlin双球的作用,进一步体会特殊化思想方法,培养学生的发散思维和严谨的逻辑思维.
情感态度与价值观
提高学生学习数学的积极性,培养他们勤于思考,敢于探索的思维习惯,使学生体会到数学的逻辑严谨的特征.
教学重难点
重点
难点
掌握并证明定理2,理解圆锥曲线的特点.
通过感知Dandlin双球作用,能掌握其定理的证明.
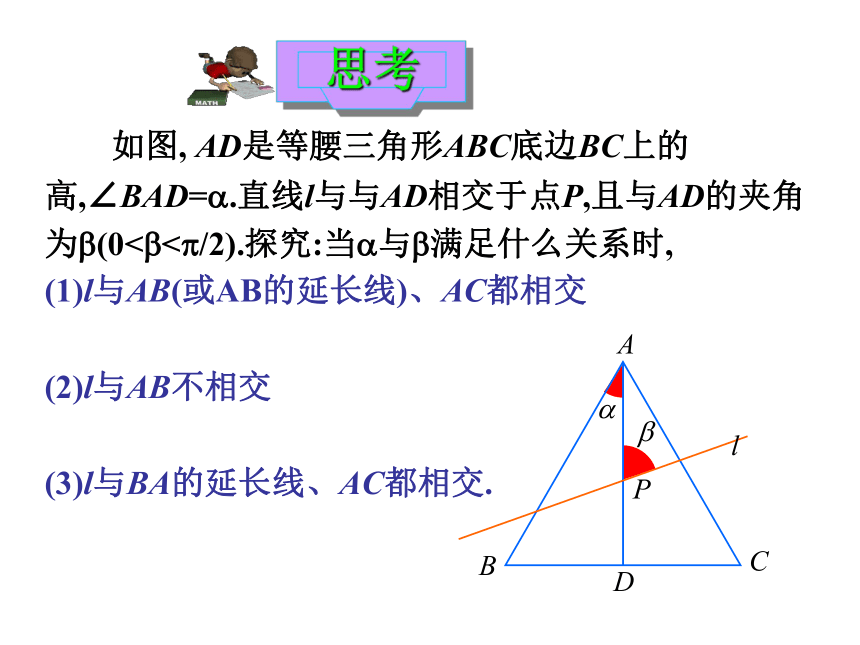
如图, AD是等腰三角形ABC底边BC上的高,∠BAD=?.直线l与与AD相交于点P,且与AD的夹角为?(0(1)l与AB(或AB的延长线)、AC都相交
(2)l与AB不相交
(3)l与BA的延长线、AC都相交.
A
B
C
D
P
?
?
l
思考
(1)当?>?时,l与AB(或AB的延长线)、AC都相交
(2)当?=?时,l与AB不相交
(3)当?解析:
推广
A
B
C
D
P
l
等腰三角形拓广为圆锥直线拓广为平面
截得图形有什么变化?
探究
如果用一个平面截一个正圆锥(两边可以无限延伸),而且这个平面不通过圆锥的顶点,会出现如下情况:
1.平面与圆锥的一母线平行
抛物线
2.平面与圆锥的一半相交
椭圆
截圆锥上部分所得图形也是一样!
3.平面与圆锥的两部分都相交
双曲线
截圆锥另一侧所得图形也是一样!
知识要点
定理2:
见如下.
定理2
在空间中,取直线l为轴,直线l?与l相交于O点,夹角为?,l?围绕l旋转得到以O为顶点,l?为母线的圆锥面.任取平面?,若它与轴l的交角为?(当?与l平行时,记?=0),则
(1)?>?,平面?与圆锥的交线为椭圆;
(2)?=?,平面?与圆锥的交线为抛物线;
(3)?在圆锥内部嵌入Dandelin双球
两球与平面?的切点分别为F1,F2,
与圆锥相切于圆S1,S2
在截口上任取一点P,连接PF1,PF2.过P作母线交S1于Q1,交S2于Q2,于是PQ1是从P到上方球的两条切线,
∴PF1=PQ1
同理,PF2=PQ2
∴PF1+PF2=PQ1+PQ2
=Q1Q2
=定值
由椭圆定义得,以F1,F2为焦点的椭圆
(1)找出椭圆的准线;
(2)探讨P到焦点F1的距离与到两平面交线m的距离之比.
上面一个Dandelin球与圆锥面的交线为圆S,记圆S所在平面为??.设?与??的交线为m.在椭圆上任取一点P,连接PF1.在?中过P作m的垂线,垂足为A.过P作??的垂线,垂足为B,连接AB,则AB是PA在平面??上的射影.
探究
m⊥AB
∠PAB为平面?与??所成的二面角的平面角
在Rt△ABP中,∠APB=?
PB=PAcos?
设过P的母线与圆S交于点Q1,
则在Rt△PQ1B中,∠Q1PB=?
PB=PQ1cos?=PF1cos?
椭圆准线
m
椭圆离心率
结论
知识要点
椭圆的结构特点
任意一点到两个定点(椭圆的两个焦点)距离之和的绝对值为常数.
当? 平面?与圆锥的两部分相交.在圆锥的两部分分别嵌Dandelin球,与平面?的两个切点分别是F1、F2,与圆锥两部分截得的圆分别为S1、S2。
探究
在截口上任取一点P,连接PF1、PF2.过点P和圆锥的顶点O作母线,分别与两个球相切于Q1,Q2,
PF1=PQ1,
PF2=PQ2,
|PF1-PF2|=|PQ1-PQ2|
=Q1Q2
=定值
知识要点
双曲线的结构特点
任意一点到两个定点(双曲线的两个焦点)距离之差的绝对值为常数.
课堂小结
1、定理2
在空间中,取直线l为轴,直线l?与l相交于O点,夹角为?,l?围绕l旋转得到以O为顶点,l?为母线的圆锥面.任取平面?,若它与轴l的交角为?(当?与l平行时,记?=0),则
(1)?>?,平面?与圆锥的交线为椭圆;
(2)?=?,平面?与圆锥的交线为抛物线;
(3)?2、椭圆的结构特点
任意一点到两个定点(椭圆的两个焦点)距离之和的绝对值为常数.
3、双曲线的结构特点
任意一点到两个定点(双曲线的两个焦点)距离之差的绝对值为常数.
1、如下图,指出圆锥被平面所截得图形是什么?
课堂练习
解析
截面是一个圆
新课导入
Dandelin(1794-1847) 丹德林,比利时人. 出生于巴黎附近的布尔日,曾在列日、纳缪尔和柳基赫等地工作.他是比利时科学院院士.丹德林主要研究代数和几何.
Dandelin(1794-1847)
事迹 :
1. 在代数方面,他于1826年提出了一种求方程根的近似方法,与罗巴切夫斯基、格雷菲提出的方法相似.
2. 在几何方面,他于1822年证明了关于圆锥曲线与圆锥的关系的一个十分有趣的定理,后来,这个球面被称为丹德林球面.
平面与圆锥相截所产生的图形?
探究
动动脑
什么图形呢?
3.3 平面与圆锥面的截线
教学目标
探究定理2的证明并掌握其定理,理解圆锥曲线的结构特点.
知识与能力
过程与方法
通过探究定理2的证明过程,感知Dandlin双球的作用,进一步体会特殊化思想方法,培养学生的发散思维和严谨的逻辑思维.
情感态度与价值观
提高学生学习数学的积极性,培养他们勤于思考,敢于探索的思维习惯,使学生体会到数学的逻辑严谨的特征.
教学重难点
重点
难点
掌握并证明定理2,理解圆锥曲线的特点.
通过感知Dandlin双球作用,能掌握其定理的证明.
如图, AD是等腰三角形ABC底边BC上的高,∠BAD=?.直线l与与AD相交于点P,且与AD的夹角为?(0(1)l与AB(或AB的延长线)、AC都相交
(2)l与AB不相交
(3)l与BA的延长线、AC都相交.
A
B
C
D
P
?
?
l
思考
(1)当?>?时,l与AB(或AB的延长线)、AC都相交
(2)当?=?时,l与AB不相交
(3)当?解析:
推广
A
B
C
D
P
l
等腰三角形拓广为圆锥直线拓广为平面
截得图形有什么变化?
探究
如果用一个平面截一个正圆锥(两边可以无限延伸),而且这个平面不通过圆锥的顶点,会出现如下情况:
1.平面与圆锥的一母线平行
抛物线
2.平面与圆锥的一半相交
椭圆
截圆锥上部分所得图形也是一样!
3.平面与圆锥的两部分都相交
双曲线
截圆锥另一侧所得图形也是一样!
知识要点
定理2:
见如下.
定理2
在空间中,取直线l为轴,直线l?与l相交于O点,夹角为?,l?围绕l旋转得到以O为顶点,l?为母线的圆锥面.任取平面?,若它与轴l的交角为?(当?与l平行时,记?=0),则
(1)?>?,平面?与圆锥的交线为椭圆;
(2)?=?,平面?与圆锥的交线为抛物线;
(3)?在圆锥内部嵌入Dandelin双球
两球与平面?的切点分别为F1,F2,
与圆锥相切于圆S1,S2
在截口上任取一点P,连接PF1,PF2.过P作母线交S1于Q1,交S2于Q2,于是PQ1是从P到上方球的两条切线,
∴PF1=PQ1
同理,PF2=PQ2
∴PF1+PF2=PQ1+PQ2
=Q1Q2
=定值
由椭圆定义得,以F1,F2为焦点的椭圆
(1)找出椭圆的准线;
(2)探讨P到焦点F1的距离与到两平面交线m的距离之比.
上面一个Dandelin球与圆锥面的交线为圆S,记圆S所在平面为??.设?与??的交线为m.在椭圆上任取一点P,连接PF1.在?中过P作m的垂线,垂足为A.过P作??的垂线,垂足为B,连接AB,则AB是PA在平面??上的射影.
探究
m⊥AB
∠PAB为平面?与??所成的二面角的平面角
在Rt△ABP中,∠APB=?
PB=PAcos?
设过P的母线与圆S交于点Q1,
则在Rt△PQ1B中,∠Q1PB=?
PB=PQ1cos?=PF1cos?
椭圆准线
m
椭圆离心率
结论
知识要点
椭圆的结构特点
任意一点到两个定点(椭圆的两个焦点)距离之和的绝对值为常数.
当? 平面?与圆锥的两部分相交.在圆锥的两部分分别嵌Dandelin球,与平面?的两个切点分别是F1、F2,与圆锥两部分截得的圆分别为S1、S2。
探究
在截口上任取一点P,连接PF1、PF2.过点P和圆锥的顶点O作母线,分别与两个球相切于Q1,Q2,
PF1=PQ1,
PF2=PQ2,
|PF1-PF2|=|PQ1-PQ2|
=Q1Q2
=定值
知识要点
双曲线的结构特点
任意一点到两个定点(双曲线的两个焦点)距离之差的绝对值为常数.
课堂小结
1、定理2
在空间中,取直线l为轴,直线l?与l相交于O点,夹角为?,l?围绕l旋转得到以O为顶点,l?为母线的圆锥面.任取平面?,若它与轴l的交角为?(当?与l平行时,记?=0),则
(1)?>?,平面?与圆锥的交线为椭圆;
(2)?=?,平面?与圆锥的交线为抛物线;
(3)?2、椭圆的结构特点
任意一点到两个定点(椭圆的两个焦点)距离之和的绝对值为常数.
3、双曲线的结构特点
任意一点到两个定点(双曲线的两个焦点)距离之差的绝对值为常数.
1、如下图,指出圆锥被平面所截得图形是什么?
课堂练习
解析
截面是一个圆
