人教A版高中数学选修4-1 第二讲 二 圆内接四边形的性质与判定定理 上课课件(共28张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-1 第二讲 二 圆内接四边形的性质与判定定理 上课课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 455.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 20:45:55 | ||
图片预览





文档简介
(共28张PPT)
旧知回顾
如果多边形的所有顶点都在一个圆上,那么这个多边形就叫做圆内接多边形.
上面的这个圆叫做多边形的外接圆.
D
A
B
C
圆内接多边形和多边形的外接圆如何定义的?
课题导入
A
B
C
A
B
C
D
是否有内接四边形?
探究
A
B
C
D
A
B
D
C
A
B
D
C
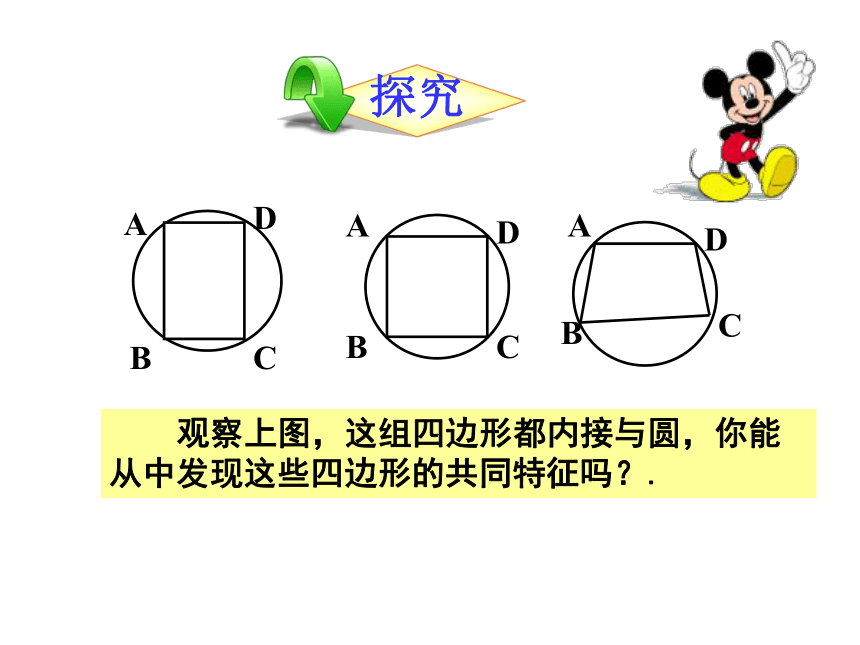
观察上图,这组四边形都内接与圆,你能从中发现这些四边形的共同特征吗?.
2.2 圆内接四边形的性质与判定定理
A
B
C
D
A
B
D
C
A
B
D
C
教学目标
理解和掌握圆的内接四边形的性质定理以及判定定理及推论,并能够用性质定理和判定定理解决有关的几何问题.
知识与能力
过程与方法
学习并领会圆的内接四边形性质定理的证明推导过程,应用圆的内接四边形性质解决几何问题过程,使学生体会和掌握“分类”和“反证法”这两种数学思想在几何证明中的作用,培养学生的发散思维和严谨的逻辑思维.
情感态度与价值观
提高学生学习数学的积极性,培养他们勤于思考,敢于探索的思维习惯,使学生体会到数学的逻辑严谨的特征.
教学重难点
重点
难点
掌握圆的内接四边形性质定理,内接四边形的判定定理及推论.
圆的内接四边形的性质及其判定的几何应用.
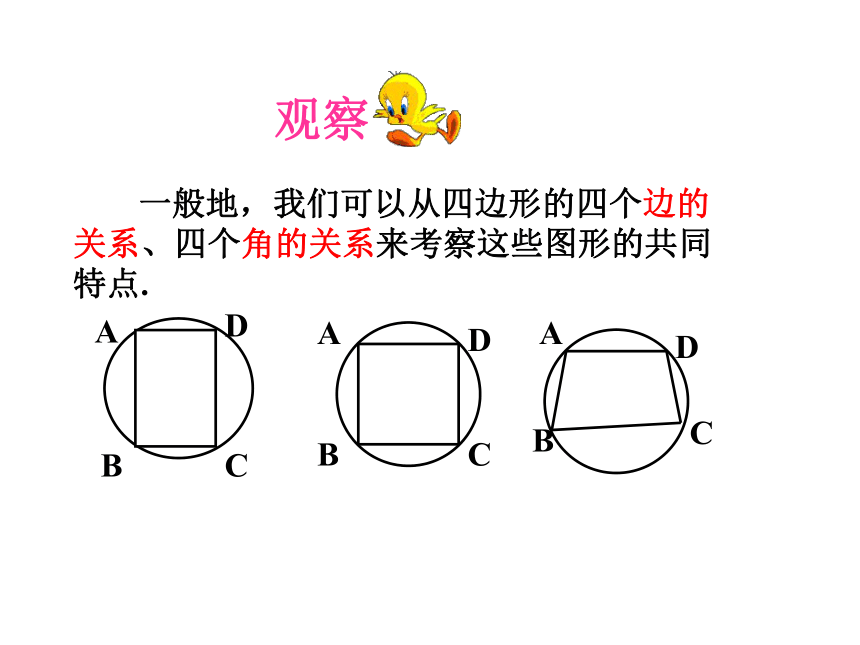
一般地,我们可以从四边形的四个边的关系、四个角的关系来考察这些图形的共同特点.
A
B
C
D
A
B
D
C
A
B
D
C
观察
圆内接四边形四个角关系
1.首先考察内接四边形的四个角:
显然,四个角都是圆周角,因此可以借助圆周角定理来研究. 如图
连接OA,OC,
∴∠B=1/2 , ∠D=1/2 .
∵ + = 360°,
∴∠B+∠D=180°.
同理可得: ∠A +∠C=180°.
B
C
D
A
.O
知识要点
圆内接四边形的性质:
定理1 圆的内接四边形的对角互补 .
圆内接四边形四个角关系
2.从补角来考虑内接四边形的四个角:
如图:
将AB延长到点E,得如图,
∵ ∠ABC+∠EBC=180° .
∴∠EBC=∠D.
B
C
D
A
.O
E
又∵ ∠ABC+∠D=180° .
知识要点
圆内接四边形的性质:
定理2 圆的内接四边形的外角等于它的 内角的对角 .
小练习
已知:如图圆O1和圆O2相交于E,F 两点,直线DC、 AB 与两圆分别相交.
A
B
C
D
E
F
.O1
.O2
问:(1)图中有几个内接四边形?
(2)四边形AFED和四边形FBCE的外角分别是什么?
(1)两个
(2)∠BEF ∠EFC
∠AEF ∠EFD
讨论
圆的内接四边形的对角互补.
讨论:如果一个四边形的对角互补,那么是否可以推出这个四边形存在外接圆?
思 考
圆内接四边形判定定理?
假设四边形ABCD中, ∠B+ ∠D=180°.
求证:A、B、C、D在同一圆周上.
分析:
根据不在同一直线上的三点确定一个圆,所以可以经过A、B、C三点做圆O,如果能证明圆O过点D,那么就证明了结论.
显然,圆O与点D有且只有三种位置关系:
(1)点D在圆外;
(2)点D在圆内;
(3)点D在圆上;只要证明只有(3)成立即可.
证明:
(1)假设点D在外部,设E使AD与圆周的交点,连接EC.
则有∠AEC+ ∠B=180°.由题设∠D+ ∠B=180°
所以∠D =∠AEC.这与“三角形的外角大于任一不相邻的内角”矛盾,故点D不在圆外.
A
B
C
D
E
.O
(2)假设点D在内部,设AD的延长线必与圆相交,设交点为E,连接EC.
则有∠E+ ∠B=180°.由题设∠ADC+ ∠B=180°
所以∠ADC =∠E.这与“三角形的外角大于任一不相邻的内角”矛盾,故点D不在圆内.
A
B
C
D
E
.O
综上所述:点D不能在圆外,也不能在圆内,根据有且只有三种可能,所以得:
点D只能在圆上,即A、B、C、D共圆.
结论
圆内接四边形的判定定理
知识要点
圆内接四边形判定定理:
如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.
知识要点
推论:
如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆。
课堂小结
定理 1 圆的内接四边形的对角互补.
1、圆内接四边形的性质定理
定理 2 圆内接四边形的外角等于它的内角的对角.
2、圆内接四边形判定定理
如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.
推论 如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.
1、已知的斜边的两个端点分别在轴、轴的正半轴上移动,顶点与原点分别在的两侧,则点的轨迹是( )
A.圆 B.线段 C. 射线 D.一段圆弧
B
如图,∵∠CAB+ ∠ COB=1800
∴四边形是圆内接四边形,则∠COA= ∠CBA ,并且是定值,∴不管怎样移动,直线的斜率不变,又由题意,可得动点的轨迹是线段.
课堂练习
解析
X
Y
A
B
C
O
2、若两条直线(a+2)x+(1-a)y-3=0,(a-1)x+(2a+3)y+2=0与两坐标轴围成的四边形有一个外接圆,则实数a等于?
∵两条直线与两坐标轴围成的四边形有一个外接圆,则有对角互补,又两坐标轴互相垂直,∴这两直线垂直,即
(a+2)(a-1)+(1-a)(2a+3)=0,即a2=1
∴ a=±1.
解:
3、过点(-1,0)作圆(x-1)2+(y-2)2=1的两切线,设两切点为A、B,圆心为C,则过A、B、C的圆方程( )
A.x2+(y-1)2=2
B.x2+(y-1)2=1
C. (x-1)2+y2=4
D.(x-1)2+y2=1
解析
∵PA⊥AC, PB⊥BC, ∴P、A、B、C四点共圆且PC为直径,故圆方程为:x2+(y-1)2=2
A
4、直线l1:2x-5y+20=0和l2:mx-2y-10=0与两坐标围成的四边形有外接圆,则求实数m值.
因为圆内接四边形的对角互补,又两坐标轴互相垂直,故l1⊥l2,
于是
解得 m=-5.
解析
5、如图,已知四边形是圆内接四边形,是⊙的直径,且EB⊥AD,AD与BC得延长线相交于F,
求证:
证明:
连结 AC, ∵∠ACB=∠DAB
∴弧AB=弧BD,∴∠ACB=∠DAB.
∵四边形ABCD是圆内接四边形,
∴∠FCD=∠DAB, ∠FDC=∠ABC. ∴ ∠ACB=∠FCD.
∴△ABC与△ABC相似.
∴即证.
旧知回顾
如果多边形的所有顶点都在一个圆上,那么这个多边形就叫做圆内接多边形.
上面的这个圆叫做多边形的外接圆.
D
A
B
C
圆内接多边形和多边形的外接圆如何定义的?
课题导入
A
B
C
A
B
C
D
是否有内接四边形?
探究
A
B
C
D
A
B
D
C
A
B
D
C
观察上图,这组四边形都内接与圆,你能从中发现这些四边形的共同特征吗?.
2.2 圆内接四边形的性质与判定定理
A
B
C
D
A
B
D
C
A
B
D
C
教学目标
理解和掌握圆的内接四边形的性质定理以及判定定理及推论,并能够用性质定理和判定定理解决有关的几何问题.
知识与能力
过程与方法
学习并领会圆的内接四边形性质定理的证明推导过程,应用圆的内接四边形性质解决几何问题过程,使学生体会和掌握“分类”和“反证法”这两种数学思想在几何证明中的作用,培养学生的发散思维和严谨的逻辑思维.
情感态度与价值观
提高学生学习数学的积极性,培养他们勤于思考,敢于探索的思维习惯,使学生体会到数学的逻辑严谨的特征.
教学重难点
重点
难点
掌握圆的内接四边形性质定理,内接四边形的判定定理及推论.
圆的内接四边形的性质及其判定的几何应用.
一般地,我们可以从四边形的四个边的关系、四个角的关系来考察这些图形的共同特点.
A
B
C
D
A
B
D
C
A
B
D
C
观察
圆内接四边形四个角关系
1.首先考察内接四边形的四个角:
显然,四个角都是圆周角,因此可以借助圆周角定理来研究. 如图
连接OA,OC,
∴∠B=1/2 , ∠D=1/2 .
∵ + = 360°,
∴∠B+∠D=180°.
同理可得: ∠A +∠C=180°.
B
C
D
A
.O
知识要点
圆内接四边形的性质:
定理1 圆的内接四边形的对角互补 .
圆内接四边形四个角关系
2.从补角来考虑内接四边形的四个角:
如图:
将AB延长到点E,得如图,
∵ ∠ABC+∠EBC=180° .
∴∠EBC=∠D.
B
C
D
A
.O
E
又∵ ∠ABC+∠D=180° .
知识要点
圆内接四边形的性质:
定理2 圆的内接四边形的外角等于它的 内角的对角 .
小练习
已知:如图圆O1和圆O2相交于E,F 两点,直线DC、 AB 与两圆分别相交.
A
B
C
D
E
F
.O1
.O2
问:(1)图中有几个内接四边形?
(2)四边形AFED和四边形FBCE的外角分别是什么?
(1)两个
(2)∠BEF ∠EFC
∠AEF ∠EFD
讨论
圆的内接四边形的对角互补.
讨论:如果一个四边形的对角互补,那么是否可以推出这个四边形存在外接圆?
思 考
圆内接四边形判定定理?
假设四边形ABCD中, ∠B+ ∠D=180°.
求证:A、B、C、D在同一圆周上.
分析:
根据不在同一直线上的三点确定一个圆,所以可以经过A、B、C三点做圆O,如果能证明圆O过点D,那么就证明了结论.
显然,圆O与点D有且只有三种位置关系:
(1)点D在圆外;
(2)点D在圆内;
(3)点D在圆上;只要证明只有(3)成立即可.
证明:
(1)假设点D在外部,设E使AD与圆周的交点,连接EC.
则有∠AEC+ ∠B=180°.由题设∠D+ ∠B=180°
所以∠D =∠AEC.这与“三角形的外角大于任一不相邻的内角”矛盾,故点D不在圆外.
A
B
C
D
E
.O
(2)假设点D在内部,设AD的延长线必与圆相交,设交点为E,连接EC.
则有∠E+ ∠B=180°.由题设∠ADC+ ∠B=180°
所以∠ADC =∠E.这与“三角形的外角大于任一不相邻的内角”矛盾,故点D不在圆内.
A
B
C
D
E
.O
综上所述:点D不能在圆外,也不能在圆内,根据有且只有三种可能,所以得:
点D只能在圆上,即A、B、C、D共圆.
结论
圆内接四边形的判定定理
知识要点
圆内接四边形判定定理:
如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.
知识要点
推论:
如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆。
课堂小结
定理 1 圆的内接四边形的对角互补.
1、圆内接四边形的性质定理
定理 2 圆内接四边形的外角等于它的内角的对角.
2、圆内接四边形判定定理
如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.
推论 如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.
1、已知的斜边的两个端点分别在轴、轴的正半轴上移动,顶点与原点分别在的两侧,则点的轨迹是( )
A.圆 B.线段 C. 射线 D.一段圆弧
B
如图,∵∠CAB+ ∠ COB=1800
∴四边形是圆内接四边形,则∠COA= ∠CBA ,并且是定值,∴不管怎样移动,直线的斜率不变,又由题意,可得动点的轨迹是线段.
课堂练习
解析
X
Y
A
B
C
O
2、若两条直线(a+2)x+(1-a)y-3=0,(a-1)x+(2a+3)y+2=0与两坐标轴围成的四边形有一个外接圆,则实数a等于?
∵两条直线与两坐标轴围成的四边形有一个外接圆,则有对角互补,又两坐标轴互相垂直,∴这两直线垂直,即
(a+2)(a-1)+(1-a)(2a+3)=0,即a2=1
∴ a=±1.
解:
3、过点(-1,0)作圆(x-1)2+(y-2)2=1的两切线,设两切点为A、B,圆心为C,则过A、B、C的圆方程( )
A.x2+(y-1)2=2
B.x2+(y-1)2=1
C. (x-1)2+y2=4
D.(x-1)2+y2=1
解析
∵PA⊥AC, PB⊥BC, ∴P、A、B、C四点共圆且PC为直径,故圆方程为:x2+(y-1)2=2
A
4、直线l1:2x-5y+20=0和l2:mx-2y-10=0与两坐标围成的四边形有外接圆,则求实数m值.
因为圆内接四边形的对角互补,又两坐标轴互相垂直,故l1⊥l2,
于是
解得 m=-5.
解析
5、如图,已知四边形是圆内接四边形,是⊙的直径,且EB⊥AD,AD与BC得延长线相交于F,
求证:
证明:
连结 AC, ∵∠ACB=∠DAB
∴弧AB=弧BD,∴∠ACB=∠DAB.
∵四边形ABCD是圆内接四边形,
∴∠FCD=∠DAB, ∠FDC=∠ABC. ∴ ∠ACB=∠FCD.
∴△ABC与△ABC相似.
∴即证.
