人教A版高中数学选修4-4 第二讲 参数方程 一 曲线的参数方程 上课课件(共43张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-4 第二讲 参数方程 一 曲线的参数方程 上课课件(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 603.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 20:48:01 | ||
图片预览











文档简介
(共43张PPT)
2.1曲线的参数方程
2.1.1参数方程的概念
2.1.2圆的参数方程
2.1.3参数方程和普通方程的互化
探究
某救援飞机给灾区投放救援物,已知飞机离地面有500米,飞机以100m/s的速度作水平直线运动,为事救援物准确落于灾区指定地面,飞行员应如何确定投放时机呢?
导入新课
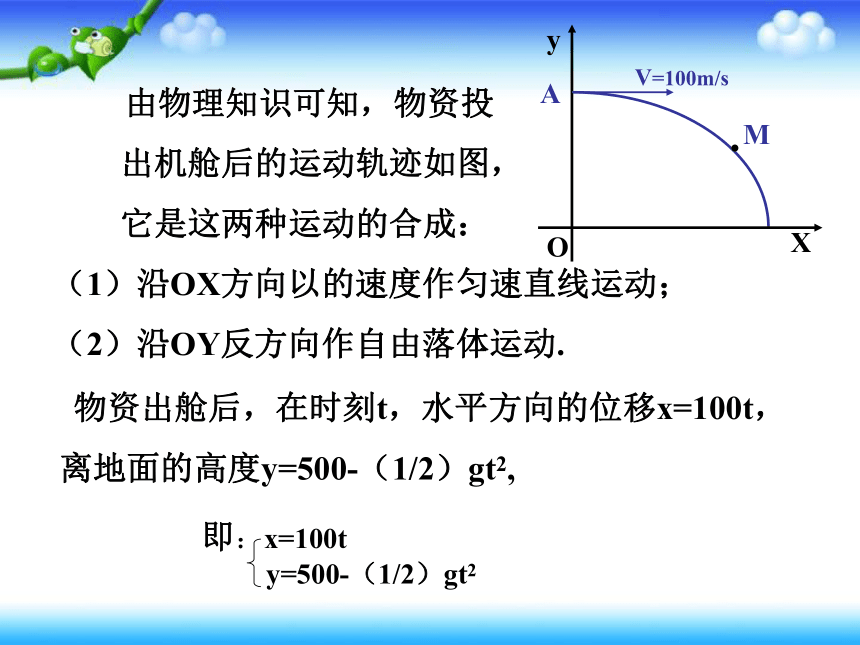
X
y
O
A
M
.
V=100m/s
由物理知识可知,物资投
出机舱后的运动轨迹如图,
它是这两种运动的合成:
(1)沿OX方向以的速度作匀速直线运动;
(2)沿OY反方向作自由落体运动.
物资出舱后,在时刻t,水平方向的位移x=100t,
离地面的高度y=500-(1/2)gt2,
即:x=100t
y=500-(1/2)gt2
在t的取值范围内,给定t的值,就能确定 x,y的值,即:当t确定时,点M的位置就确定.
由上所述,公式
可以确定物资投放后的每一个时刻的位置,还可以确定物资投放的时机.
x=100t
y=500-(1/2)gt2
2.1.1参数方程的概念
知识与能力
1.了解参数方程的基本概念.
2.学会从实际生活的问题抽象出数学模型.
教学目标
过程与方法
情感态度与价值观
能够在已有的经验(生活经验,数学学习经验)的基础上,更好的了解参数方程的概念.
从实际问题中感知参数方程的作用.
重点
难点
参数的概念.
1.根据问题的条件引进适当的参数.
2.参数方程与普通方程的同异点.
教学重难点
一般地,在平面直角坐标系中如果
曲线上任意一点的坐标x 、y都是某个变数t 的函数,
即:
并且对于t的每一个允许值,由上述方程组所确定的点M(x,y)都在这条曲线上,那么上述方程组 就叫做这条曲线的参数方程.联系x、y变数t叫做参变数,简称参数.
参数方程与普通方程的同异点
(1)普通方程F(x,y)=0直接给出了曲线上点x, y的坐标之间的关系,由于一个方程中含有两个变量,因此自由变量有一个,而且给定其中任意一个变量的值,都可以由方程F(x,y)=0确定另一个变量的值;
(2)参数方程 借助参数t,间接
给出曲线上点的坐标x ,y之间的关系,由于
是两个方程中含有x,y,t三个变量,因此自
由变量也只有一个,而且给定参数t的值,
就可以由方程组 求出唯一对应x, y
的值,而且大多数情况下,参数方程中
参数的变化范围是有限制的.
例题
1.已知曲线C的参数方程是
x=3t,
y=2t2+1 (t为参数)
(1)判断点M1(0,1),M2(5,4)与曲线C的位置关系;
(2)已知点M1(6,a)在曲线C上,求a的值.
解:(1)把点M1(0,1)的坐标代入方程组中,得t=0,所以点M1在曲线C上;同理,把点M2(5,4)代入方程组中,得
5=3t 此方程组无解,即点不在曲线上.
4=2t2+1
(2)因为点M2(6,a)在曲线C上,
所以: 6=3t
a=2t2+1 解得t=2,a=9
上节课我们学习了参数方程的概念,也了解参方程和普通方程的同异之处.现在大家来想想:圆心在原点半径为r的圆,我们用什么样的参数方程去表示它呢?
思考。。。
导入新课
2.1.2圆的参数方程
知识与能力
1.了解圆的参数方程的概念;
2.培养同学们分析曲线的能力.
教学目标
过程与方法
情感态度与价值观
1.培养学生探究现实生活中大量存在的规律.
2.让学生意识到同一问题可有多种求解方法.
1.掌握用参数方程的思想方法来认识问题.
重点
难点
1.分析圆的参数方程的几何意义.
2.圆的参数方程.
1.根据问题的条件引进适当的参数.
2.选择适当的参数写出它们的参数方
3.体会圆的参数方程的意义.
教学重难点
并且对于 的每一个允许值,由
方程组①所确定的点P(x,y)在圆O上.
我们把方程组①叫做圆心在原点、
半径为 r的圆的参数方程,为参数.
①
x
y
o
)
r
2.已知点P是圆上的一个动点,该圆的半径为4,点Q(12,0)是X轴上的一定点,当点P在圆上运动时,求线段PQ的中点M的轨迹.
Q
M
P
O
4
例题
Q
M
P
O
4
解:设点M的坐标为 ,点P的坐标为 ,取 ,圆O的参数方程为:
( 为参数)
(1)
Q
M
P
O
4
又因为点M是线段PQ的中点,点P的
坐标为 ,点Q的坐标为Q(12,0) ,
根据线段的中点坐标公式得:
(2)
连立(1)(2)式,解得:
例题
3.已知圆的直径AB上有两点C,D,|AB|=10, |AC|=|BD|=4,P为圆上一点, 求|PC|+|PD|的最大值.
x
y
o
P
C
D
A
B
x
y
o
P
C
D
A
B
解:如图建立直角坐标系,因为
|AB|=10,所以圆的参数方程为
( 为参数)
因为|AC|=|BD|=4,所以C,D的坐标为 C(-1,0), D(1,0)
因为点P在圆上,所以可求得点P的坐标为:
所以,
当 时,
所以 的最大值为 .
2.1.3参数方程和普通方程的互化
你能由以下参数方程
直观地看出此方程代表的是什么类型的曲线吗?
动动脑哦...
导入新课
知识与能力
熟练掌握参数方程和普通方程的互化的方法.
教学目标
过程与方法
情感态度与价值观
1.培养学生探究现实生活中大量存在的规律.
2.体会从多角度看待同一问题的意义.
掌握用参数方程的思想方法来认识问题.
重点
难点
参数方程和普通方程的互化.
1.根据几何性质选取适当的参数建立曲线的参数方程 .
2.参数方程和普通方程的互化.
教学重难点
似乎直接判断该方程代表的曲线类型并 不容易,但如果将参数方程转化为我们熟悉的普通方程,即:
现在,我们可以很直观地看出该方程
代表的曲线是圆心 ,半径为1的圆 .
(圆心随a的变化而移动)
将曲线的参数方程化为普通方程,有利于识别曲线的类型.
例题
1.把下列参数方程化为普通方程,并说明它们各表示什么曲线.
(1) x=3-2t,
y=-1-4t (t为参数)
(2) x=t+1/t
y=t-1/t (t为参数)
解:(1)由x=3-2t,得
将此式代入y=-1-4t ,得y=-7+2x,
即2x-7-y=0(直线)
(2)由x=t+1/t, y=t-1/t 得
所以
(双曲线)
为常数,
化为普通方程:
(1)
例题
2.分别在下列两种情况下, 把参数方程
(2) 为常数, 为参数
为参数
解:(1)当 时,
即 ,当 时,
而
即
,
(2)当 时, ,
即
当 时, ,
即
当 时,得
,
即:
得
即:
将参数方程化为普通方程的常用方法有:
(1)代入法,先由一个方程求出参数的
表达式(用直角坐标变量表示),
再代入另一个方程.(如例1)
归纳
(2)利用代数或三角函数中的恒等式
消去参数,例如对于参数方程
如果 是常数, 是参数,
那么可以利用公式 ;
如果 是常数, 是参数,
那么适当变形后可以利用
1.已知动圆方程
为参数),那么圆心的轨迹是( )
A.椭圆 B.椭圆的一部分
C.抛物线 D.抛物线的一部分
解:圆心轨迹的参数方程为:
消去参数得 :
D
课堂练习
2.把方程 化为以 为参数的参数
方程是( )
A B C D
D
3.长为3a的线段的端点分别在x、y轴上滑动,
M为AB的一个三等分点,则M的轨迹方程是
___________________(提示:利用等分比公式)
1、若直线 ( 为参数)与
直线 ( 为参数)垂直,则
___ .
.
解: ,得
针对性练习
2、点P(1,0)到
曲线
(其中参数t∈R)
上的点的最短距离为( )
A、0 B、1 C、 D、2
解:消去参数t,知曲线为开口向右的
抛物线y2=4x,知点P(1,0)恰是抛物线的焦点,
设M(x0,y0)是抛物线上任一点,
由焦半径公式得,|PM|=1+x0≥1,即当M在
原点时,最短距离为1,故选B.
B
2.1曲线的参数方程
2.1.1参数方程的概念
2.1.2圆的参数方程
2.1.3参数方程和普通方程的互化
探究
某救援飞机给灾区投放救援物,已知飞机离地面有500米,飞机以100m/s的速度作水平直线运动,为事救援物准确落于灾区指定地面,飞行员应如何确定投放时机呢?
导入新课
X
y
O
A
M
.
V=100m/s
由物理知识可知,物资投
出机舱后的运动轨迹如图,
它是这两种运动的合成:
(1)沿OX方向以的速度作匀速直线运动;
(2)沿OY反方向作自由落体运动.
物资出舱后,在时刻t,水平方向的位移x=100t,
离地面的高度y=500-(1/2)gt2,
即:x=100t
y=500-(1/2)gt2
在t的取值范围内,给定t的值,就能确定 x,y的值,即:当t确定时,点M的位置就确定.
由上所述,公式
可以确定物资投放后的每一个时刻的位置,还可以确定物资投放的时机.
x=100t
y=500-(1/2)gt2
2.1.1参数方程的概念
知识与能力
1.了解参数方程的基本概念.
2.学会从实际生活的问题抽象出数学模型.
教学目标
过程与方法
情感态度与价值观
能够在已有的经验(生活经验,数学学习经验)的基础上,更好的了解参数方程的概念.
从实际问题中感知参数方程的作用.
重点
难点
参数的概念.
1.根据问题的条件引进适当的参数.
2.参数方程与普通方程的同异点.
教学重难点
一般地,在平面直角坐标系中如果
曲线上任意一点的坐标x 、y都是某个变数t 的函数,
即:
并且对于t的每一个允许值,由上述方程组所确定的点M(x,y)都在这条曲线上,那么上述方程组 就叫做这条曲线的参数方程.联系x、y变数t叫做参变数,简称参数.
参数方程与普通方程的同异点
(1)普通方程F(x,y)=0直接给出了曲线上点x, y的坐标之间的关系,由于一个方程中含有两个变量,因此自由变量有一个,而且给定其中任意一个变量的值,都可以由方程F(x,y)=0确定另一个变量的值;
(2)参数方程 借助参数t,间接
给出曲线上点的坐标x ,y之间的关系,由于
是两个方程中含有x,y,t三个变量,因此自
由变量也只有一个,而且给定参数t的值,
就可以由方程组 求出唯一对应x, y
的值,而且大多数情况下,参数方程中
参数的变化范围是有限制的.
例题
1.已知曲线C的参数方程是
x=3t,
y=2t2+1 (t为参数)
(1)判断点M1(0,1),M2(5,4)与曲线C的位置关系;
(2)已知点M1(6,a)在曲线C上,求a的值.
解:(1)把点M1(0,1)的坐标代入方程组中,得t=0,所以点M1在曲线C上;同理,把点M2(5,4)代入方程组中,得
5=3t 此方程组无解,即点不在曲线上.
4=2t2+1
(2)因为点M2(6,a)在曲线C上,
所以: 6=3t
a=2t2+1 解得t=2,a=9
上节课我们学习了参数方程的概念,也了解参方程和普通方程的同异之处.现在大家来想想:圆心在原点半径为r的圆,我们用什么样的参数方程去表示它呢?
思考。。。
导入新课
2.1.2圆的参数方程
知识与能力
1.了解圆的参数方程的概念;
2.培养同学们分析曲线的能力.
教学目标
过程与方法
情感态度与价值观
1.培养学生探究现实生活中大量存在的规律.
2.让学生意识到同一问题可有多种求解方法.
1.掌握用参数方程的思想方法来认识问题.
重点
难点
1.分析圆的参数方程的几何意义.
2.圆的参数方程.
1.根据问题的条件引进适当的参数.
2.选择适当的参数写出它们的参数方
3.体会圆的参数方程的意义.
教学重难点
并且对于 的每一个允许值,由
方程组①所确定的点P(x,y)在圆O上.
我们把方程组①叫做圆心在原点、
半径为 r的圆的参数方程,为参数.
①
x
y
o
)
r
2.已知点P是圆上的一个动点,该圆的半径为4,点Q(12,0)是X轴上的一定点,当点P在圆上运动时,求线段PQ的中点M的轨迹.
Q
M
P
O
4
例题
Q
M
P
O
4
解:设点M的坐标为 ,点P的坐标为 ,取 ,圆O的参数方程为:
( 为参数)
(1)
Q
M
P
O
4
又因为点M是线段PQ的中点,点P的
坐标为 ,点Q的坐标为Q(12,0) ,
根据线段的中点坐标公式得:
(2)
连立(1)(2)式,解得:
例题
3.已知圆的直径AB上有两点C,D,|AB|=10, |AC|=|BD|=4,P为圆上一点, 求|PC|+|PD|的最大值.
x
y
o
P
C
D
A
B
x
y
o
P
C
D
A
B
解:如图建立直角坐标系,因为
|AB|=10,所以圆的参数方程为
( 为参数)
因为|AC|=|BD|=4,所以C,D的坐标为 C(-1,0), D(1,0)
因为点P在圆上,所以可求得点P的坐标为:
所以,
当 时,
所以 的最大值为 .
2.1.3参数方程和普通方程的互化
你能由以下参数方程
直观地看出此方程代表的是什么类型的曲线吗?
动动脑哦...
导入新课
知识与能力
熟练掌握参数方程和普通方程的互化的方法.
教学目标
过程与方法
情感态度与价值观
1.培养学生探究现实生活中大量存在的规律.
2.体会从多角度看待同一问题的意义.
掌握用参数方程的思想方法来认识问题.
重点
难点
参数方程和普通方程的互化.
1.根据几何性质选取适当的参数建立曲线的参数方程 .
2.参数方程和普通方程的互化.
教学重难点
似乎直接判断该方程代表的曲线类型并 不容易,但如果将参数方程转化为我们熟悉的普通方程,即:
现在,我们可以很直观地看出该方程
代表的曲线是圆心 ,半径为1的圆 .
(圆心随a的变化而移动)
将曲线的参数方程化为普通方程,有利于识别曲线的类型.
例题
1.把下列参数方程化为普通方程,并说明它们各表示什么曲线.
(1) x=3-2t,
y=-1-4t (t为参数)
(2) x=t+1/t
y=t-1/t (t为参数)
解:(1)由x=3-2t,得
将此式代入y=-1-4t ,得y=-7+2x,
即2x-7-y=0(直线)
(2)由x=t+1/t, y=t-1/t 得
所以
(双曲线)
为常数,
化为普通方程:
(1)
例题
2.分别在下列两种情况下, 把参数方程
(2) 为常数, 为参数
为参数
解:(1)当 时,
即 ,当 时,
而
即
,
(2)当 时, ,
即
当 时, ,
即
当 时,得
,
即:
得
即:
将参数方程化为普通方程的常用方法有:
(1)代入法,先由一个方程求出参数的
表达式(用直角坐标变量表示),
再代入另一个方程.(如例1)
归纳
(2)利用代数或三角函数中的恒等式
消去参数,例如对于参数方程
如果 是常数, 是参数,
那么可以利用公式 ;
如果 是常数, 是参数,
那么适当变形后可以利用
1.已知动圆方程
为参数),那么圆心的轨迹是( )
A.椭圆 B.椭圆的一部分
C.抛物线 D.抛物线的一部分
解:圆心轨迹的参数方程为:
消去参数得 :
D
课堂练习
2.把方程 化为以 为参数的参数
方程是( )
A B C D
D
3.长为3a的线段的端点分别在x、y轴上滑动,
M为AB的一个三等分点,则M的轨迹方程是
___________________(提示:利用等分比公式)
1、若直线 ( 为参数)与
直线 ( 为参数)垂直,则
___ .
.
解: ,得
针对性练习
2、点P(1,0)到
曲线
(其中参数t∈R)
上的点的最短距离为( )
A、0 B、1 C、 D、2
解:消去参数t,知曲线为开口向右的
抛物线y2=4x,知点P(1,0)恰是抛物线的焦点,
设M(x0,y0)是抛物线上任一点,
由焦半径公式得,|PM|=1+x0≥1,即当M在
原点时,最短距离为1,故选B.
B
