人教A版高中数学选修4-4 第一讲 坐标系 四 柱坐标系和球坐标系简介 上课课件(共33张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-4 第一讲 坐标系 四 柱坐标系和球坐标系简介 上课课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 518.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 20:49:37 | ||
图片预览










文档简介
(共33张PPT)
1.4柱坐标系与球坐标系简介
1.4.1柱 坐 标 系
1.4.2球 坐 标 系
我们知道,建立平面直角坐标后,平面上的点可以用直角坐标表示;建立极坐标后,平面上的点可以用极坐标表示,那么,是否能建立空间极坐标系,用极坐标表示空间的点呢?
想一想
新课导入
1.4.1柱坐标系
教学目标
知识与能力
1.使同学们对简单柱坐标,球坐标有初步的认识。
2.学会从实际生活的问题抽象出数学模型
过程与方法
情感态度与价值观
1.培养学生学会从“感性认识”到“理性认识”过程中获取新知。
2.感知柱坐标方程在现实中的应用。
从实际问题中感知柱坐标,球坐标方程的应用。
教学重难点
重点
难点
举例说明柱坐标,球坐标在日常生活中的应用。
柱坐标,球坐标的表示。
1. 某圆形体育场被平均分为十二个区域,第一排与体育场中心O的距离为300,每相邻两排的距离为1m,每层看台的高度为0.6m,现在需要确定看台上第九区第三排正中的位置A,如何去描述这个位置呢?
我们以圆形体育场中心O为极点,选取以O为端点的射线OX为极轴,在地平面上建立极坐标系。
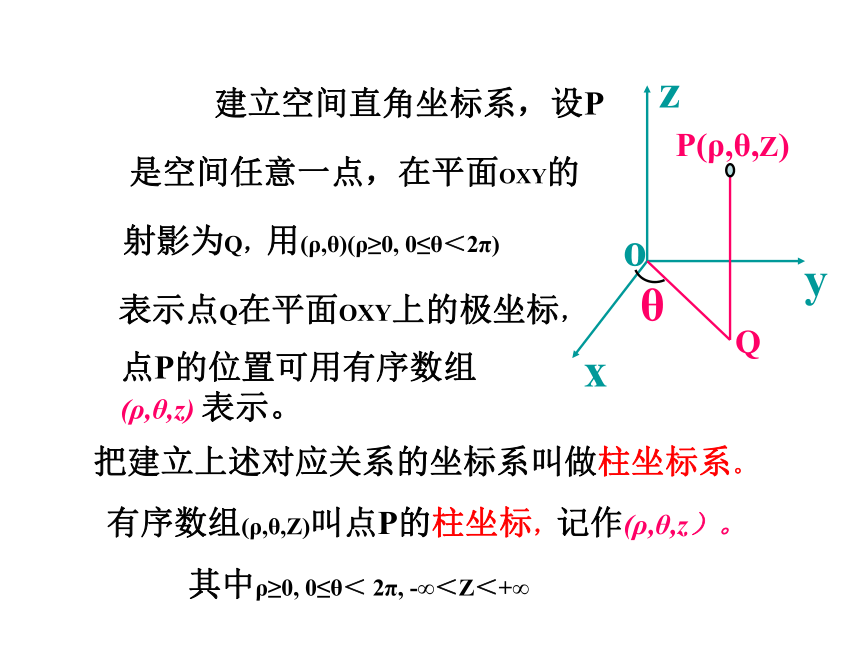
建立空间直角坐标系,设P
是空间任意一点,在平面OXY的
射影为Q,用(ρ,θ)(ρ≥0, 0≤θ<2π)
表示点Q在平面OXY上的极坐标,
点P的位置可用有序数组
(ρ,θ,z) 表示。
把建立上述对应关系的坐标系叫做柱坐标系。
有序数组(ρ,θ,Z)叫点P的柱坐标,记作(ρ,θ,z)。
其中ρ≥0, 0≤θ< 2π, -∞<Z<+∞
x
y
z
o
P(ρ,θ,Z)
Q
θ
空间点P的直角坐标(x, y, z)与柱坐标(ρ,θ,Z)之间的变换公式为:
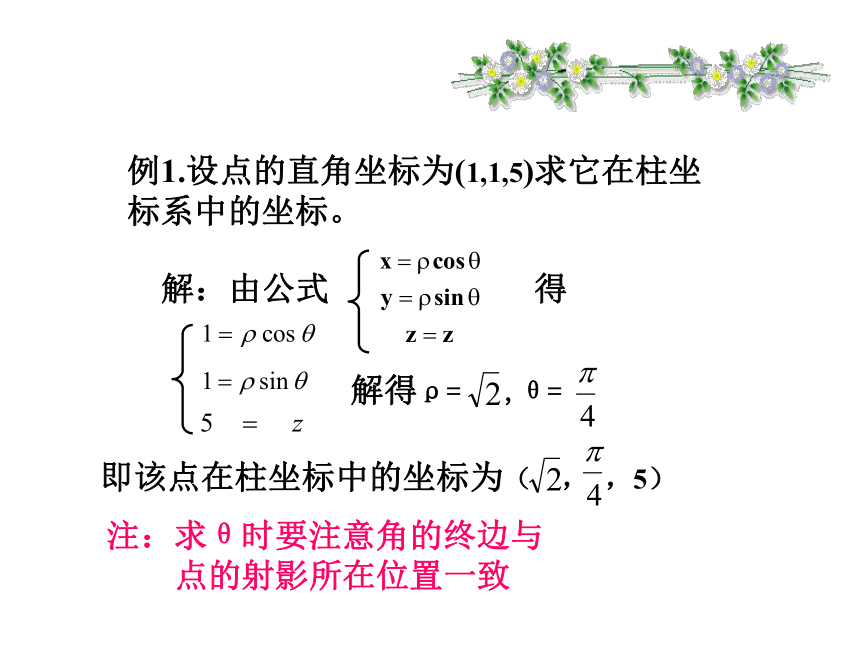
例1.设点的直角坐标为(1,1,5)求它在柱坐标系中的坐标。
解:由公式 得
解得ρ= ,θ=
即该点在柱坐标中的坐标为( , ,5)
注:求θ时要注意角的终边与
点的射影所在位置一致
1.4.2球坐标系
“神舟七号”载人飞船的又一次成功发射,实现了我国空间技术发展里程碑意义的重大跨越,是中国人民攀登世界科技高峰的又一大壮举. 那你们曾想过,在航空航天领域,人们是怎样确定航天器的准确位置的呢?
人们确定航天器某一时刻的具体位置,
是根据某一时刻航天器到地球表面的
距离r,以及航天器所处位置的经度
和纬度 ,从而用有序数组
表示航天器的具体位置
那么,如何建立坐标系才能方便得出
r,,的值,从而确定它的位置呢?
x
y
z
o
P
Q
θ
r
φ
如图,设P是空间任意一点,
OP与OZ轴正向所夹的角为φ.
设P在oxy平面上的射影为Q,
Ox轴按逆时针方向旋转到
这样点P的位置就可以用有序数组(r,φ,θ)表示。
连接OP,记| OP |=r,
OQ时所转过的最小正角为θ.
我们把建立上述对应关系的坐标系叫做
球坐标系 (或空间极坐标系) 。
(r,φ,θ)
例2. 已知点A的球坐标为
(2, , ),求它的直角坐标。
解:将点A的球坐标代入公
即点A的直角坐标为:
得
有序数组(r,φ,θ)叫做点P的球坐标,
其中
空间点P的直角坐标(x, y, z)与球坐标(r,φ,θ)之间的变换关系为
例3.设点的球坐标为(4, , ),求它的直角坐标。
解:将点的球坐标代入公式
即:
该点的直角坐标为:
所以
1、设 OA是球 O的半径M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆 C ,若圆的面积等于 ,求球O的表面积。
针对性练习
解:设球半径为 ,圆的半径为
因为
由
得 ,故球的表面积等于
坐标系
平面极坐标系
柱坐标系
球坐标系
极坐标系
坐标系
伸缩变换
简单曲线的极坐标方程
极坐标与直角坐标 的互化
本讲知识总结
坐 标 系
(1)回顾在平面直角坐标系中刻画点的未知的方法,体会坐标系的作用。
(2)通过具体例子,了解在平面直角坐标系中的伸缩变换作用下的变化情况。
(3)能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面及角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化中。
(4)能在极坐标系中给出简单图形的方程,通过比较这些图形在极坐标系和平面直角坐标系中的方程,体会在用方程刻画平面图形时选择适当坐标系的意义。
(5)借助具体事例了解在柱坐标系和球坐标系中刻画空间中点的位置的方法,并与空间直角坐标系中刻画点的位置的方法比较,体会它们的区别。
坐标系是联系形与数的桥梁,
利用坐标系可以实现几何问题与
代数问题的相互转化,不同的坐标系
有不同的特点,在实际问题中,
我们要根据问题的
特点选择适当的坐标系,借助
坐标系可以方便,简捷地研究问题。
一、选择题
1.极坐标方程 化为直角坐标方程的形式为( )
B.
C
D.
A
2.在极坐标系中,如果等边三角形的两个顶点是A(2,),B(2,),那么顶点C的坐标可能是( )
课堂练习
3.已知点A,B的极坐标为 和 则A和B之间的距离等于( )
4.在同一坐标系中,将曲线
变成曲线 的伸缩变换是( )
A
B
C
D
5.柱坐标 对应的直角坐标是( )
6.极坐标系内曲线 上的动点P 与定点 的最近距离是( )
二.填空题
7.在极坐标系中,以 为圆心,为半径的圆的方程是_______
8.若直线的极坐标方程为
则极点到该线的距离是_______
9.在极坐标戏中,过点 和点 的直线的倾斜角是_________
10.球坐标系 对应的点的直角坐标是_______
三.解答题
11.通过平面直角坐标系中的平移变换与伸缩变换,可以把椭圆
变为中心在原点的单位圆,求上述平移变换与伸缩变换,以及这两种变换的合成的变换。
12.在平面直角坐标系中,以原点为极点,X轴正半轴为极轴建立极坐标系,设椭圆的长轴长为10,中心为(3,0),一个焦点在直角坐标原点。
(1)求椭圆的直角坐标方程,并化为极坐标方程。
(2)当椭圆的过直角坐标原点的弦
长为 时,求弦所在直线的直角坐标方程。
参考答案
一.选择题:1.B 2.B 3. 4.B 5.A 6.A
二.填空题:
三.解答题:
11.先通过平移变换
由上述两种变换合成的变换是:
把椭圆
变为椭圆
再通过伸缩变换
把椭圆
变为单位圆
12.(1)由已知,得到
故 ,所以,椭圆的直角坐
标方程为
由于 ,代入上式得到
即
即 所以,
椭圆的极坐标方程为
12.(2)设过直角坐标原点的弦的倾斜角为 ,弦的两端分别为
则有
由于
所以,
即
所以 或 ,即直线的
直角坐标方程为 或
1.4柱坐标系与球坐标系简介
1.4.1柱 坐 标 系
1.4.2球 坐 标 系
我们知道,建立平面直角坐标后,平面上的点可以用直角坐标表示;建立极坐标后,平面上的点可以用极坐标表示,那么,是否能建立空间极坐标系,用极坐标表示空间的点呢?
想一想
新课导入
1.4.1柱坐标系
教学目标
知识与能力
1.使同学们对简单柱坐标,球坐标有初步的认识。
2.学会从实际生活的问题抽象出数学模型
过程与方法
情感态度与价值观
1.培养学生学会从“感性认识”到“理性认识”过程中获取新知。
2.感知柱坐标方程在现实中的应用。
从实际问题中感知柱坐标,球坐标方程的应用。
教学重难点
重点
难点
举例说明柱坐标,球坐标在日常生活中的应用。
柱坐标,球坐标的表示。
1. 某圆形体育场被平均分为十二个区域,第一排与体育场中心O的距离为300,每相邻两排的距离为1m,每层看台的高度为0.6m,现在需要确定看台上第九区第三排正中的位置A,如何去描述这个位置呢?
我们以圆形体育场中心O为极点,选取以O为端点的射线OX为极轴,在地平面上建立极坐标系。
建立空间直角坐标系,设P
是空间任意一点,在平面OXY的
射影为Q,用(ρ,θ)(ρ≥0, 0≤θ<2π)
表示点Q在平面OXY上的极坐标,
点P的位置可用有序数组
(ρ,θ,z) 表示。
把建立上述对应关系的坐标系叫做柱坐标系。
有序数组(ρ,θ,Z)叫点P的柱坐标,记作(ρ,θ,z)。
其中ρ≥0, 0≤θ< 2π, -∞<Z<+∞
x
y
z
o
P(ρ,θ,Z)
Q
θ
空间点P的直角坐标(x, y, z)与柱坐标(ρ,θ,Z)之间的变换公式为:
例1.设点的直角坐标为(1,1,5)求它在柱坐标系中的坐标。
解:由公式 得
解得ρ= ,θ=
即该点在柱坐标中的坐标为( , ,5)
注:求θ时要注意角的终边与
点的射影所在位置一致
1.4.2球坐标系
“神舟七号”载人飞船的又一次成功发射,实现了我国空间技术发展里程碑意义的重大跨越,是中国人民攀登世界科技高峰的又一大壮举. 那你们曾想过,在航空航天领域,人们是怎样确定航天器的准确位置的呢?
人们确定航天器某一时刻的具体位置,
是根据某一时刻航天器到地球表面的
距离r,以及航天器所处位置的经度
和纬度 ,从而用有序数组
表示航天器的具体位置
那么,如何建立坐标系才能方便得出
r,,的值,从而确定它的位置呢?
x
y
z
o
P
Q
θ
r
φ
如图,设P是空间任意一点,
OP与OZ轴正向所夹的角为φ.
设P在oxy平面上的射影为Q,
Ox轴按逆时针方向旋转到
这样点P的位置就可以用有序数组(r,φ,θ)表示。
连接OP,记| OP |=r,
OQ时所转过的最小正角为θ.
我们把建立上述对应关系的坐标系叫做
球坐标系 (或空间极坐标系) 。
(r,φ,θ)
例2. 已知点A的球坐标为
(2, , ),求它的直角坐标。
解:将点A的球坐标代入公
即点A的直角坐标为:
得
有序数组(r,φ,θ)叫做点P的球坐标,
其中
空间点P的直角坐标(x, y, z)与球坐标(r,φ,θ)之间的变换关系为
例3.设点的球坐标为(4, , ),求它的直角坐标。
解:将点的球坐标代入公式
即:
该点的直角坐标为:
所以
1、设 OA是球 O的半径M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆 C ,若圆的面积等于 ,求球O的表面积。
针对性练习
解:设球半径为 ,圆的半径为
因为
由
得 ,故球的表面积等于
坐标系
平面极坐标系
柱坐标系
球坐标系
极坐标系
坐标系
伸缩变换
简单曲线的极坐标方程
极坐标与直角坐标 的互化
本讲知识总结
坐 标 系
(1)回顾在平面直角坐标系中刻画点的未知的方法,体会坐标系的作用。
(2)通过具体例子,了解在平面直角坐标系中的伸缩变换作用下的变化情况。
(3)能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面及角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化中。
(4)能在极坐标系中给出简单图形的方程,通过比较这些图形在极坐标系和平面直角坐标系中的方程,体会在用方程刻画平面图形时选择适当坐标系的意义。
(5)借助具体事例了解在柱坐标系和球坐标系中刻画空间中点的位置的方法,并与空间直角坐标系中刻画点的位置的方法比较,体会它们的区别。
坐标系是联系形与数的桥梁,
利用坐标系可以实现几何问题与
代数问题的相互转化,不同的坐标系
有不同的特点,在实际问题中,
我们要根据问题的
特点选择适当的坐标系,借助
坐标系可以方便,简捷地研究问题。
一、选择题
1.极坐标方程 化为直角坐标方程的形式为( )
B.
C
D.
A
2.在极坐标系中,如果等边三角形的两个顶点是A(2,),B(2,),那么顶点C的坐标可能是( )
课堂练习
3.已知点A,B的极坐标为 和 则A和B之间的距离等于( )
4.在同一坐标系中,将曲线
变成曲线 的伸缩变换是( )
A
B
C
D
5.柱坐标 对应的直角坐标是( )
6.极坐标系内曲线 上的动点P 与定点 的最近距离是( )
二.填空题
7.在极坐标系中,以 为圆心,为半径的圆的方程是_______
8.若直线的极坐标方程为
则极点到该线的距离是_______
9.在极坐标戏中,过点 和点 的直线的倾斜角是_________
10.球坐标系 对应的点的直角坐标是_______
三.解答题
11.通过平面直角坐标系中的平移变换与伸缩变换,可以把椭圆
变为中心在原点的单位圆,求上述平移变换与伸缩变换,以及这两种变换的合成的变换。
12.在平面直角坐标系中,以原点为极点,X轴正半轴为极轴建立极坐标系,设椭圆的长轴长为10,中心为(3,0),一个焦点在直角坐标原点。
(1)求椭圆的直角坐标方程,并化为极坐标方程。
(2)当椭圆的过直角坐标原点的弦
长为 时,求弦所在直线的直角坐标方程。
参考答案
一.选择题:1.B 2.B 3. 4.B 5.A 6.A
二.填空题:
三.解答题:
11.先通过平移变换
由上述两种变换合成的变换是:
把椭圆
变为椭圆
再通过伸缩变换
把椭圆
变为单位圆
12.(1)由已知,得到
故 ,所以,椭圆的直角坐
标方程为
由于 ,代入上式得到
即
即 所以,
椭圆的极坐标方程为
12.(2)设过直角坐标原点的弦的倾斜角为 ,弦的两端分别为
则有
由于
所以,
即
所以 或 ,即直线的
直角坐标方程为 或
