人教版七年级数学 下册 6.2 立方根 教案(表格式)
文档属性
| 名称 | 人教版七年级数学 下册 6.2 立方根 教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 54.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 11:36:26 | ||
图片预览


文档简介
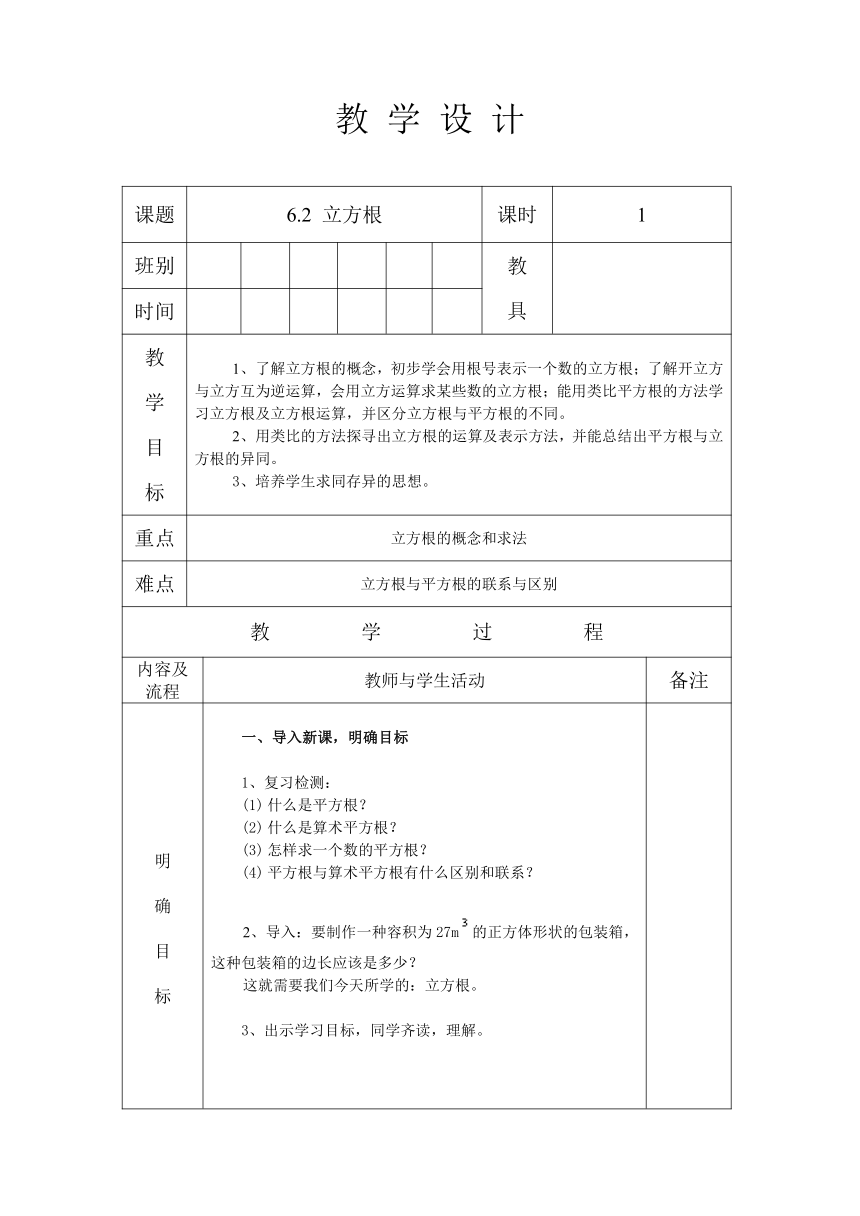
教 学 设 计
课题 6.2 立方根 课时 1
班别 教 具
时间
教 学 目 标 了解立方根的概念,初步学会用根号表示一个数的立方根;了解开立方与立方互为逆运算,会用立方运算求某些数的立方根;能用类比平方根的方法学习立方根及立方根运算,并区分立方根与平方根的不同。 用类比的方法探寻出立方根的运算及表示方法,并能总结出平方根与立方根的异同。 3、培养学生求同存异的思想。
重点 立方根的概念和求法
难点 立方根与平方根的联系与区别
教 学 过 程
内容及流程 教师与学生活动 备注
明 确 目 标 导入新课,明确目标 复习检测: 什么是平方根? 什么是算术平方根? 怎样求一个数的平方根? 平方根与算术平方根有什么区别和联系? 2、导入:要制作一种容积为27m的正方体形状的包装箱,这种包装箱的边长应该是多少? 这就需要我们今天所学的:立方根。 3、出示学习目标,同学齐读,理解。
内容及流程 教师与学生活动 备注
实 施 目 标 二、自主预习 梳理新知 1.立方根的概念: 如果一个数的立方等于a,这个数就叫做a的 .(也叫做数a的 ). 换句话说,如果 ,那么x叫做a的立方根或三次方根. 记作: .读作“ ”, 其中a是 ,3是 ,且根指数3 省略(填能或不能),否则与平方根混淆. 2.开立方:求一个数的 的运算叫做开立方, 与开立方互为逆运算 3.立方根的性质:正数的立方根是 数,负数的立方根是 数,0的立方根是 . 三、合作探究 生成能力 目标导学一:立方根的概念及性质 【类型一】 立方根的概念及性质 例1、立方根等于本身的数有________个. 解析:在正数中,1 (3)=1,在负数中,-1 (3)=-1,又0 (3)=0,∴立方根等于本身的数有1,-1,0.故填3. 方法总结:不论正数、负数还是零,都有立方根. 【类型二】 立方根与平方根的综合问题 例2:已知x-2的平方根是±2,2x+y+7的立方根是3,求x2+y2的算术平方根. 解析:根据平方根、立方根的定义和已知条件可知x-2=4,2x+y+7=27,从而解出x,y,最后代入x2+y2,求其算术平方根即可. 解:∵x-2的平方根是±2,∴x-2=4,∴x=6.∵2x+y+7的立方根是3,∴2x+y+7=27.把x=6代入解得y=8,∴x2+y2=62+82=100.∴x2+y2的算术平方根为10. 方法总结:本题先根据平方根和立方根的定义,运用方程思想列方程求出x,y的值,再根据算术平方根的定义求出x2+y2的算术平方根.
内容及流程 教师与学生活动 备注
实 施 目 标 【类型三】 立方根的实际应用 例3: 已知球的体积公式是V=3 (4)πr3(r为球的半径,π取3.14),现已知一个小皮球的体积是113.04cm3,求这个小皮球的半径r. 解析:将公式变形为r3=4π (3V),从而求r. 解:由V=3 (4)πr3,得r3=4π (3V),∴r=4π (3V).∵V=113.04cm3,π取3.14,∴r≈4×3.14 (3×113.04)=27 (3)=3(cm). 答:这个小皮球的半径r约为3cm. 方法总结:解此题的关键是灵活应用球体积公式,并将公式适当变形. 目标导学二:开立方运算 例5:如果要生产这种容积为50L的圆柱形热水器,使它的高等于底面直径的2倍,这种容器的底面直径应取多少?(结果保留两个有效数字) 问题:有多大呢? (这里可以让学生回忆前面学习过程中讨论有多大时的方法)。 所以 …… 如此循环下去,可以得到更精确的的近似值,它是一个无限不循环小数,=一3.684 031 49……事实上,很多有理数的立方根都是无限不循环小数.我们用有理数近似地表示它们. 四、课堂总结 今天我们学习了立方根的概念以及立方根的计算方法,希望同学们把立方根与平方根对照着学习与运用。
内容及流程 教师与学生活动 备注
检 测 目 标 1. 判断正误: (1)、25的立方根是 5 ;( ) (2)、互为相反数的两个数,它们的立方根也互为相反数;( ) (3)、任何数的立方根只有一个;( ) (4)、如果一个数的平方根与其立方根相同,则 这个数是1;( ) (5)、如果一个数的立方根是这个数的本身,那么这个数一定是零;( ) (6)、一个数的立方根不是正数就是负数.( ) (7)、–64没有立方根.( ) 2、(1) 64的平方根是________立方根是________. (2) 的立方根是________. (3) 是_______的立方根.
板 书 设 计 6.2 立方根 1.每个数a都只有一个立方根,记为“a (3)”,读作“三次根号a”. 2.正数的立方根是正数;0的立方根是0;负数的立方根是负数. 3.求一个数a的立方根的运算叫做开立方,其中a叫做被开方数.开立方与立方互为逆运算.
领 导 评 课 意 见 学校检查记实
教学后记
课题 6.2 立方根 课时 1
班别 教 具
时间
教 学 目 标 了解立方根的概念,初步学会用根号表示一个数的立方根;了解开立方与立方互为逆运算,会用立方运算求某些数的立方根;能用类比平方根的方法学习立方根及立方根运算,并区分立方根与平方根的不同。 用类比的方法探寻出立方根的运算及表示方法,并能总结出平方根与立方根的异同。 3、培养学生求同存异的思想。
重点 立方根的概念和求法
难点 立方根与平方根的联系与区别
教 学 过 程
内容及流程 教师与学生活动 备注
明 确 目 标 导入新课,明确目标 复习检测: 什么是平方根? 什么是算术平方根? 怎样求一个数的平方根? 平方根与算术平方根有什么区别和联系? 2、导入:要制作一种容积为27m的正方体形状的包装箱,这种包装箱的边长应该是多少? 这就需要我们今天所学的:立方根。 3、出示学习目标,同学齐读,理解。
内容及流程 教师与学生活动 备注
实 施 目 标 二、自主预习 梳理新知 1.立方根的概念: 如果一个数的立方等于a,这个数就叫做a的 .(也叫做数a的 ). 换句话说,如果 ,那么x叫做a的立方根或三次方根. 记作: .读作“ ”, 其中a是 ,3是 ,且根指数3 省略(填能或不能),否则与平方根混淆. 2.开立方:求一个数的 的运算叫做开立方, 与开立方互为逆运算 3.立方根的性质:正数的立方根是 数,负数的立方根是 数,0的立方根是 . 三、合作探究 生成能力 目标导学一:立方根的概念及性质 【类型一】 立方根的概念及性质 例1、立方根等于本身的数有________个. 解析:在正数中,1 (3)=1,在负数中,-1 (3)=-1,又0 (3)=0,∴立方根等于本身的数有1,-1,0.故填3. 方法总结:不论正数、负数还是零,都有立方根. 【类型二】 立方根与平方根的综合问题 例2:已知x-2的平方根是±2,2x+y+7的立方根是3,求x2+y2的算术平方根. 解析:根据平方根、立方根的定义和已知条件可知x-2=4,2x+y+7=27,从而解出x,y,最后代入x2+y2,求其算术平方根即可. 解:∵x-2的平方根是±2,∴x-2=4,∴x=6.∵2x+y+7的立方根是3,∴2x+y+7=27.把x=6代入解得y=8,∴x2+y2=62+82=100.∴x2+y2的算术平方根为10. 方法总结:本题先根据平方根和立方根的定义,运用方程思想列方程求出x,y的值,再根据算术平方根的定义求出x2+y2的算术平方根.
内容及流程 教师与学生活动 备注
实 施 目 标 【类型三】 立方根的实际应用 例3: 已知球的体积公式是V=3 (4)πr3(r为球的半径,π取3.14),现已知一个小皮球的体积是113.04cm3,求这个小皮球的半径r. 解析:将公式变形为r3=4π (3V),从而求r. 解:由V=3 (4)πr3,得r3=4π (3V),∴r=4π (3V).∵V=113.04cm3,π取3.14,∴r≈4×3.14 (3×113.04)=27 (3)=3(cm). 答:这个小皮球的半径r约为3cm. 方法总结:解此题的关键是灵活应用球体积公式,并将公式适当变形. 目标导学二:开立方运算 例5:如果要生产这种容积为50L的圆柱形热水器,使它的高等于底面直径的2倍,这种容器的底面直径应取多少?(结果保留两个有效数字) 问题:有多大呢? (这里可以让学生回忆前面学习过程中讨论有多大时的方法)。 所以 …… 如此循环下去,可以得到更精确的的近似值,它是一个无限不循环小数,=一3.684 031 49……事实上,很多有理数的立方根都是无限不循环小数.我们用有理数近似地表示它们. 四、课堂总结 今天我们学习了立方根的概念以及立方根的计算方法,希望同学们把立方根与平方根对照着学习与运用。
内容及流程 教师与学生活动 备注
检 测 目 标 1. 判断正误: (1)、25的立方根是 5 ;( ) (2)、互为相反数的两个数,它们的立方根也互为相反数;( ) (3)、任何数的立方根只有一个;( ) (4)、如果一个数的平方根与其立方根相同,则 这个数是1;( ) (5)、如果一个数的立方根是这个数的本身,那么这个数一定是零;( ) (6)、一个数的立方根不是正数就是负数.( ) (7)、–64没有立方根.( ) 2、(1) 64的平方根是________立方根是________. (2) 的立方根是________. (3) 是_______的立方根.
板 书 设 计 6.2 立方根 1.每个数a都只有一个立方根,记为“a (3)”,读作“三次根号a”. 2.正数的立方根是正数;0的立方根是0;负数的立方根是负数. 3.求一个数a的立方根的运算叫做开立方,其中a叫做被开方数.开立方与立方互为逆运算.
领 导 评 课 意 见 学校检查记实
教学后记
