2020湘教版八下数学1.2直角三角形的性质与判定Ⅱ第2课时习题课件(29张PPT)
文档属性
| 名称 | 2020湘教版八下数学1.2直角三角形的性质与判定Ⅱ第2课时习题课件(29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 843.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 13:28:44 | ||
图片预览








文档简介
课件29张PPT。1.2 直角三角形的性质和判定(Ⅱ)?
第2课时1.掌握勾股定理的逆定理,会用勾股定理的逆定理判断直角三角形.
2.会运用勾股定理的逆定理解决实际问题.(重点、难点)一、勾股定理的逆定理
如图,在△ABC和Rt△A'B'C'中,AB=A'B',AC=A'C',AB2+AC2
=BC2,∠A'=90°,【思考】
1.BC与B'C'相等吗?为什么?
提示:BC=B'C'.理由如下:
在Rt△A'B'C'中,由勾股定理得A'B'2+A'C'2=B'C'2,
∵AB=A'B',AC=A'C',AB2+AC2=BC2,
∴BC2=B'C'2,∴BC=B'C'.2.你能求出∠A吗?
提示:∵BC2=B'C'2,∴BC=B'C',
∴△ABC≌△A'B'C'(SSS),
∴∠A=∠A'=90°.【总结】勾股定理的逆定理:如果三角形的三边长a,b,c满足关
系:________,那么这个三角形是直角三角形.a2+b2=c2二、勾股数
满足________的三个_____数称为勾股数.a2+b2=c2正整 (打“√”或“×”)
(1)三边长为6,8,9的三角形是直角三角形. ( )
(2)任意直角三角形的三边都满足a2+b2=c2. ( )
(3)三边平方之比为1∶1∶2的三角形是直角三角形. ( )
(4)三边长为9,12,15的三角形的面积是27. ( )
(5)1.5,2,2.5是一组勾股数. ( )×√√××知识点 1 勾股定理的逆定理?
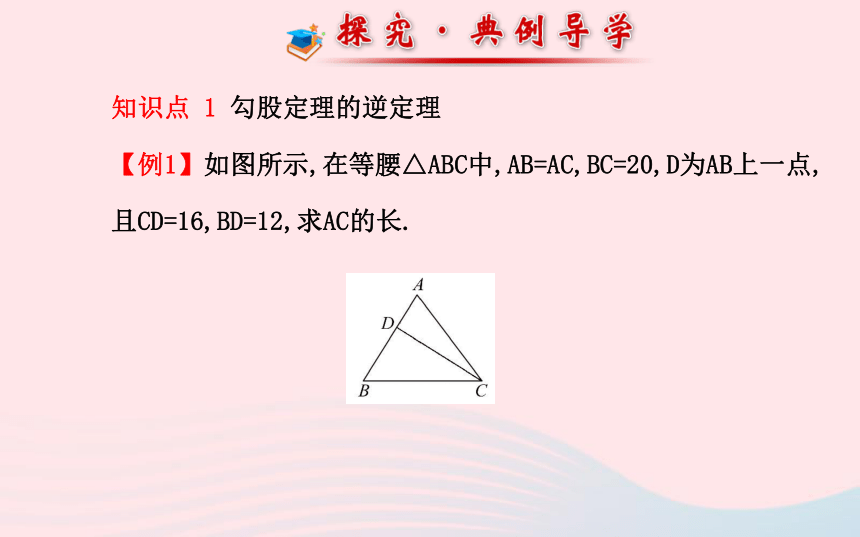
【例1】如图所示,在等腰△ABC中,AB=AC,BC=20,D为AB上一点,且CD=16,BD=12,求AC的长.【解题探究】(1)已知△BCD的三边长,你能确定它的形状吗?
提示:能,因为122+162=202,所以△BCD是直角三角形.
(2)△ACD是_____三角形.
(3)设AD=x,则AC=AB=_____.
根据勾股定理可得方程______________,
解方程得x=_____,可得AC=______.直角12+x162+x2=(12+x)2【总结提升】由三边判定直角三角形的三步法知识点 2 勾股定理的逆定理的实际应用?
【例2】B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每
小时8n mile的速度前进,乙船沿南偏东某个角度以每小时
15n mile的速度前进,2h后,甲船到M岛,乙船到P岛,两岛相距
34n mile,你知道乙船是沿哪个方向航行的吗?
【思路点拨】先判断以B,M,P三点为顶点的三角形的形状,再判
断航行的方向.【自主解答】甲船航行的距离为BM=8×2=16(n mile),
乙船航行的距离为BP=15×2=30(n mile).
∵162+302=1156,342=1156,∴BM2+BP2=MP2,
∴△MBP为直角三角形,∠MBP=90°,∴乙船是沿着南偏东30°方向航行的.【总结提升】勾股定理逆定理的实际应用的一般步骤
1.要把实际问题转化成数学问题,对于需要画图表示的,一定要从数学问题中抽象出正确的几何图形.
2.通过分析,运用勾股定理的逆定理来验证它是否为直角三角形,然后利用直角三角形的性质解决实际问题.题组一:勾股定理的逆定理
1.在△ABC中,AB=9,AC=12,BC=15,则该三角形为 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
【解析】选B.∵92+122=152,即AB2+AC2=BC2,∴由勾股定理的逆定理得此三角形是直角三角形.2.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于
( )
A.10 B.11
C.12 D.13【解析】选D.∵AD为△ABC的中线,
∴BD=5,∴BD2+AD2=AB2,
∴△ADB为直角三角形,在△ABD和△ACD中,
∴△ABD≌△ACD,∴AC=AB=13.3.已知三组数据:①2,3,4;②3,4,5;③1, ,2.分别以每组数
据中的三个数为三角形的三边长,构成直角三角形的有( )
A.② B.①② C.①③ D.②③
【解析】选D.因为22+32=4+9=13,42=16,所以22+32≠42,不能构
成直角三角形;因为32+42=9+16=25,52=25,所以32+42=52,能构成
直角三角形;因为12+( )2=1+3=4,22=4,所以12+( )2=22,能
构成直角三角形.所以能构成直角三角形的有②③.4.在△ABC中,若三边长a=n2-1,b=2n,c=n2+1,则△ABC是( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
【解析】选D.∵a2+b2=(n2-1)2+(2n)2=n4-2n2+1+4n2=
n4+2n2+1=(n2+1)2=c2.
∴△ABC是直角三角形.5.如图1、
图2是两张形状、大小完全相
同的方格纸,方格纸中的每个
小正方形的边长均为1,点A,B在小正方形的顶点上.
(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可).
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).【解析】(1)如图:(以下各图画出一个即可,答案不唯一)(2)如图:(以下各图画出一个即可,答案不唯一)题组二:勾股定理的逆定理的实际应用
1.园丁住宅小区有一块草坪如图所示.已知AB=3m,BC=4m,
CD=12m,DA=13m,且AB⊥BC,这块草坪的面积是( )
A.24m2 B.36m2 C.48m2 D.72m2【解析】选B.连接AC,则由勾股定理得AC=5m,
因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积= AB·BC+ AC·DC= (3×4+5×12)=36(m2).2.如图,做一个宽80cm,高60cm的长方形木框,需在相对角的顶点之间加一根加固木条,则木条的长为 ( )
A.90 cm B.100 cm C.105 cm D.110 cm
【解析】选B.设木条的长度为xcm,
由勾股定理得x2=802+602,
解得x=100.3.小强在操场上向东走200m后,又走了150m,再走250m回到原地.小强在操场上向东走了200m后,又走150m的方向是________.
【解析】因为2002+1502=62500=2502,所以小强走了一个直角三角形.开始他是向东走,当他再向正北或者正南走的时候,恰好构成直角.
答案:正南或正北4.如图所示,在某市的地图上有三个景点A,B,
C,已知景点A,B之间的距离为0.4cm,景点C,B
之间的距离为0.3cm,景点A,C之间的距离为
0.5cm,问以这三个景点为顶点的三角形是直角三角形吗?为什么?
【解析】因为0.32+0.42=0.52,由勾股定理的逆定理可知这个三角形一定是直角三角形.5.在新农村建设中,一农民在建房时挖了一个
地基,如图是平面图形.按建房标准,四边形
ABCD应为长方形.AB=DC=8cm,AD=BC=6cm,AC=
9cm,请你帮他看一下挖的地基是否合格.
【解析】先看∠ADC是不是直角.
在△ADC中,因为AD2+DC2=62+82=100,AC2=92=81,所以AD2+DC2≠AC2,所以△ADC不是直角三角形,所以∠ADC不是直角.但标准是长方形的四个角都应是直角,所以该农民挖的地基不合格.【想一想错在哪?】下列三角形中是直角三角形的是( )
A.三边之比为5∶6∶7 B.三边之比为9∶40∶41
C.三边之长为32,42,52 D.三边之长为13,14,15
提示:三边之长分别为3,4,5的三角形为直角三角形,而不是三边之长分别为32,42,52的三角形.
第2课时1.掌握勾股定理的逆定理,会用勾股定理的逆定理判断直角三角形.
2.会运用勾股定理的逆定理解决实际问题.(重点、难点)一、勾股定理的逆定理
如图,在△ABC和Rt△A'B'C'中,AB=A'B',AC=A'C',AB2+AC2
=BC2,∠A'=90°,【思考】
1.BC与B'C'相等吗?为什么?
提示:BC=B'C'.理由如下:
在Rt△A'B'C'中,由勾股定理得A'B'2+A'C'2=B'C'2,
∵AB=A'B',AC=A'C',AB2+AC2=BC2,
∴BC2=B'C'2,∴BC=B'C'.2.你能求出∠A吗?
提示:∵BC2=B'C'2,∴BC=B'C',
∴△ABC≌△A'B'C'(SSS),
∴∠A=∠A'=90°.【总结】勾股定理的逆定理:如果三角形的三边长a,b,c满足关
系:________,那么这个三角形是直角三角形.a2+b2=c2二、勾股数
满足________的三个_____数称为勾股数.a2+b2=c2正整 (打“√”或“×”)
(1)三边长为6,8,9的三角形是直角三角形. ( )
(2)任意直角三角形的三边都满足a2+b2=c2. ( )
(3)三边平方之比为1∶1∶2的三角形是直角三角形. ( )
(4)三边长为9,12,15的三角形的面积是27. ( )
(5)1.5,2,2.5是一组勾股数. ( )×√√××知识点 1 勾股定理的逆定理?
【例1】如图所示,在等腰△ABC中,AB=AC,BC=20,D为AB上一点,且CD=16,BD=12,求AC的长.【解题探究】(1)已知△BCD的三边长,你能确定它的形状吗?
提示:能,因为122+162=202,所以△BCD是直角三角形.
(2)△ACD是_____三角形.
(3)设AD=x,则AC=AB=_____.
根据勾股定理可得方程______________,
解方程得x=_____,可得AC=______.直角12+x162+x2=(12+x)2【总结提升】由三边判定直角三角形的三步法知识点 2 勾股定理的逆定理的实际应用?
【例2】B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每
小时8n mile的速度前进,乙船沿南偏东某个角度以每小时
15n mile的速度前进,2h后,甲船到M岛,乙船到P岛,两岛相距
34n mile,你知道乙船是沿哪个方向航行的吗?
【思路点拨】先判断以B,M,P三点为顶点的三角形的形状,再判
断航行的方向.【自主解答】甲船航行的距离为BM=8×2=16(n mile),
乙船航行的距离为BP=15×2=30(n mile).
∵162+302=1156,342=1156,∴BM2+BP2=MP2,
∴△MBP为直角三角形,∠MBP=90°,∴乙船是沿着南偏东30°方向航行的.【总结提升】勾股定理逆定理的实际应用的一般步骤
1.要把实际问题转化成数学问题,对于需要画图表示的,一定要从数学问题中抽象出正确的几何图形.
2.通过分析,运用勾股定理的逆定理来验证它是否为直角三角形,然后利用直角三角形的性质解决实际问题.题组一:勾股定理的逆定理
1.在△ABC中,AB=9,AC=12,BC=15,则该三角形为 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
【解析】选B.∵92+122=152,即AB2+AC2=BC2,∴由勾股定理的逆定理得此三角形是直角三角形.2.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于
( )
A.10 B.11
C.12 D.13【解析】选D.∵AD为△ABC的中线,
∴BD=5,∴BD2+AD2=AB2,
∴△ADB为直角三角形,在△ABD和△ACD中,
∴△ABD≌△ACD,∴AC=AB=13.3.已知三组数据:①2,3,4;②3,4,5;③1, ,2.分别以每组数
据中的三个数为三角形的三边长,构成直角三角形的有( )
A.② B.①② C.①③ D.②③
【解析】选D.因为22+32=4+9=13,42=16,所以22+32≠42,不能构
成直角三角形;因为32+42=9+16=25,52=25,所以32+42=52,能构成
直角三角形;因为12+( )2=1+3=4,22=4,所以12+( )2=22,能
构成直角三角形.所以能构成直角三角形的有②③.4.在△ABC中,若三边长a=n2-1,b=2n,c=n2+1,则△ABC是( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
【解析】选D.∵a2+b2=(n2-1)2+(2n)2=n4-2n2+1+4n2=
n4+2n2+1=(n2+1)2=c2.
∴△ABC是直角三角形.5.如图1、
图2是两张形状、大小完全相
同的方格纸,方格纸中的每个
小正方形的边长均为1,点A,B在小正方形的顶点上.
(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可).
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).【解析】(1)如图:(以下各图画出一个即可,答案不唯一)(2)如图:(以下各图画出一个即可,答案不唯一)题组二:勾股定理的逆定理的实际应用
1.园丁住宅小区有一块草坪如图所示.已知AB=3m,BC=4m,
CD=12m,DA=13m,且AB⊥BC,这块草坪的面积是( )
A.24m2 B.36m2 C.48m2 D.72m2【解析】选B.连接AC,则由勾股定理得AC=5m,
因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积= AB·BC+ AC·DC= (3×4+5×12)=36(m2).2.如图,做一个宽80cm,高60cm的长方形木框,需在相对角的顶点之间加一根加固木条,则木条的长为 ( )
A.90 cm B.100 cm C.105 cm D.110 cm
【解析】选B.设木条的长度为xcm,
由勾股定理得x2=802+602,
解得x=100.3.小强在操场上向东走200m后,又走了150m,再走250m回到原地.小强在操场上向东走了200m后,又走150m的方向是________.
【解析】因为2002+1502=62500=2502,所以小强走了一个直角三角形.开始他是向东走,当他再向正北或者正南走的时候,恰好构成直角.
答案:正南或正北4.如图所示,在某市的地图上有三个景点A,B,
C,已知景点A,B之间的距离为0.4cm,景点C,B
之间的距离为0.3cm,景点A,C之间的距离为
0.5cm,问以这三个景点为顶点的三角形是直角三角形吗?为什么?
【解析】因为0.32+0.42=0.52,由勾股定理的逆定理可知这个三角形一定是直角三角形.5.在新农村建设中,一农民在建房时挖了一个
地基,如图是平面图形.按建房标准,四边形
ABCD应为长方形.AB=DC=8cm,AD=BC=6cm,AC=
9cm,请你帮他看一下挖的地基是否合格.
【解析】先看∠ADC是不是直角.
在△ADC中,因为AD2+DC2=62+82=100,AC2=92=81,所以AD2+DC2≠AC2,所以△ADC不是直角三角形,所以∠ADC不是直角.但标准是长方形的四个角都应是直角,所以该农民挖的地基不合格.【想一想错在哪?】下列三角形中是直角三角形的是( )
A.三边之比为5∶6∶7 B.三边之比为9∶40∶41
C.三边之长为32,42,52 D.三边之长为13,14,15
提示:三边之长分别为3,4,5的三角形为直角三角形,而不是三边之长分别为32,42,52的三角形.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
