2020湘教版八下数学1.3直角三角形全等的判定习题课件(39张PPT)
文档属性
| 名称 | 2020湘教版八下数学1.3直角三角形全等的判定习题课件(39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 713.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 13:30:22 | ||
图片预览











文档简介
课件39张PPT。1.3 直角三角形全等的判定?1.掌握“HL”定理,会用“HL”定理判定两个直角三角形全等.(重点)
2.会选用合适的方法判定两个直角三角形全等.(难点)斜边、直角边定理
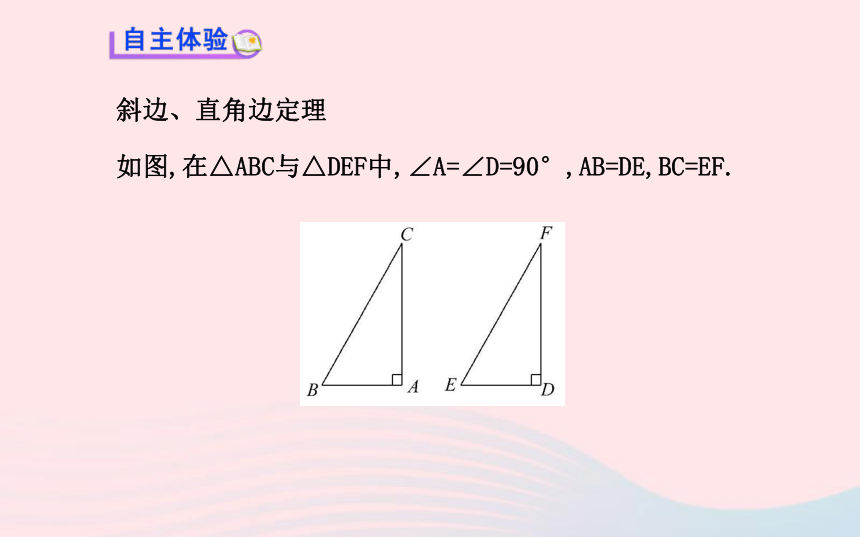
如图,在△ABC与△DEF中,∠A=∠D=90°,AB=DE,BC=EF.【思考】
(1)AC与DF相等吗?为什么?
提示:AC=DF.理由如下:
∵∠A=∠D=90°,
根据勾股定理得AB2+AC2=BC2,DE2+DF2=EF2,
又∵AB=DE,BC=EF,∴AC=DF.
(2)△ABC与△DEF全等吗?为什么?
提示:全等.∵AB=DE,BC=EF,AC=DF.
∴△ABC≌△DEF(SSS).【总结】
斜边、直角边定理:_____和一条_______对应相等的两个
直角三角形全等(可以简写成“_____________”或“___”).斜边直角边斜边、直角边HL (打“√”或“×”)
(1)“HL”定理适合所有三角形全等的判定. ( )
(2)判定两个直角三角形全等只能用“HL”定理. ( )
(3)有两条边对应相等的三角形全等. ( )
(4)一条直角边和一个锐角对应相等的三角形全等. ( )×××√知识点 1 应用“HL”证明直角三角形全等?
【例1】如图,在△ABC中,∠B=90°,AD为
∠BAC的平分线,DF⊥AC于F,DE=DC,那么
BE=CF吗?请说明理由.
【思路点拨】先下结论BE=CF,再说明理由:先证∠BAD=∠CAD,
∠B=∠AFD,得出△ABD≌△AFD,BD=FD,再证Rt△EBD≌Rt△CFD,
证得BE=CF.【自主解答】BE=CF.理由如下:
∵AD为∠BAC的平分线,∴∠BAD=∠CAD.
∵DF⊥AC,∴∠AFD=90°.
又∠B=90°,∴∠B=∠AFD.
在△ABD和△AFD中,
∴△ABD≌△AFD(AAS),∴BD=FD.在Rt△EBD和Rt△CFD中,
∴Rt△EBD≌Rt△CFD(HL),∴BE=CF.【总结提升】应用“HL”应注意的三个问题
1.“HL”是判定两个直角三角形全等的方法,对于一般的三角形不成立,在使用时一定要注意其应用的范围.
2.在书写格式上,三角形的前面必须注明“Rt”.
3.在题设中,没有指明但又是直角三角形的,必须依照定义说明或推证是直角三角形,否则不能直接应用“HL”.知识点 2 选定合适方法判定直角三角形全等?
【例2】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE.
(2)如图2,若BE
的延长线交AC于点F,且BF⊥AC,
垂足为F,∠BAC=45°,原题设其他条件不变.
求证:△AEF≌△BCF.【思路点拨】(1)根据等腰三角形三线合一的性质可得∠BDE=
∠CDE,然后利用“边角边”证明△BDE和△CDE全等即可.
(2)先判定△ABF为等腰直角三角形,再根据等腰直角三角形的
两直角边相等可得AF=BF,再根据同角的余角相等求出∠EAF=
∠CBF,然后利用“角边角”证明△AEF和△BCF全等即可.【自主解答】(1)∵AB=AC,D是BC的中点,
∴∠BDE=∠CDE=90°,
在△BDE和△CDE中,
∴△BDE≌△CDE(SAS),
∴BE=CE.(2)∵∠BAC=45°,BF⊥AF,
∴△ABF为等腰直角三角形,∴AF=BF,
∵AB=AC,点D是BC的中点,∴AD⊥BC,
∴∠EAF+∠C=90°,
∵BF⊥AC,∴∠CBF+∠C=90°,
∴∠EAF=∠CBF,
在△AEF和△BCF中,
∴△AEF≌△BCF(ASA).【总结提升】判定直角三角形全等的方法选择题组一:应用“HL”证明直角三角形全等
1.如图,四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为 ( )
A.145° B.130° C.110° D.70°【解析】选C.∵∠ABC=∠ADC=90°,
∴在Rt△ABC与Rt△ADC中,
CB=CD,AC=AC,
∴△ABC≌△ADC,又∠BAC=35°,
∴∠ACD=∠ACB=55°,
∴∠BCD=110°.2.如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是 ( )
A.∠DAE=∠CBE
B.CE=DE
C.△DAE与△CBE不一定全等
D.∠1=∠2【解析】选C.∵AD=BC,∠C=∠D=90°,∠DEA=∠CEB,
∴△DAE≌△CBE(C选项不正确),
∴∠DAE=∠CBE(A选项正确),
CE=DE(B选项正确),
∵AD=BC,∠C=∠D=90°,AB=BA,
∴△ABC≌△BAD.
∴∠1=∠2(D选项正确).3.如图,长方形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有 ( )
A.3对 B.4对 C.5对 D.6对
【解析】选B.图中全等的直角三角形有:△AED≌△FEC,
△BDC≌△FDC≌△DBA,共4对.【变式训练】如图,AC,BD是长方形ABCD的
对角线,过点D作DE∥AC交BC的延长线于E,
则图中与△ABC全等的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【解析】选D.与△ABC全等的三角形为△ADC,△BAD,△DCB,
△DCE共4个.4.如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为 ;若添加条件AC=EC,则可以用 判定全等.【解析】∵AB⊥BD,AB∥ED,∴ED⊥BD,
∴∠B=∠D=90°;
①又∵AB=ED,
∴在△ABC和△EDC中,当BC=DC时,△ABC≌△EDC(SAS);
②在Rt△ABC和Rt△EDC中,AB=ED,AC=EC,由“HL”定理可得Rt△ABC≌Rt△EDC(HL).
答案:BC=DC HL5.如图,△ABC中,∠ABC=45°,AD⊥BC于D,
点E在AD上,且BE=AC,求证:DE=CD.
【证明】∵∠ABC=45°,AD⊥BC,
∴AD=BD,∠BDE=∠ADC=90°.
又∵BE=AC,
∴△BDE≌△ADC(HL).
∴DE=CD.6.如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线,交AC于点E.求证:AE=ED.【证明】连接BE,∵DE为BC的垂线,∴∠BDE=90°.
∴∠BDE=∠A.
在Rt△BDE和Rt△BAE中,
∴Rt△BDE≌Rt△BAE(HL),∴AE=ED.题组二:选定合适方法判定直角三角形全等
1.如图,E是正方形ABCD的边DC上一点,过点A
作FA⊥AE交CB的延长线于点F.若AB=4,则四
边形AFCE的面积是 ( )
A.4 B.8 C.16 D.无法计算【解析】选C.∵∠EAD+∠BAE=90°,
∠FAB+∠BAE=90°,∴∠FAB=∠EAD.
∵四边形ABCD为正方形,
∴AB=AD,∠D=∠ABF=90°.
在△ABF和△ADE中,
∴△ABF≌△ADE(ASA),
∴四边形AFCE的面积与正方形ABCD的面积相等,
∴S四边形AFCE=S正方形ABCD=AB2=16.2.把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
(1) ,∠A=∠D(ASA).
(2)AC=DF, (SAS).
(3)AB=DE,BC=EF( ).
(4)AC=DF, (HL).
(5)∠A=∠D,BC=EF( ).
(6) ,AC=DF(AAS).【解析】要利用题中的“直角三角形有一个角是直角”的条件,找准对应元素及三角形全等的判定方法.
答案:(1)AC=DF (2)CB=FE (3)HL
(4)AB=DE (5)AAS (6)∠B=∠E3.如图,A,B,C三点在同
一条直线上,∠A=∠C=90°,AB=CD,请添加
一个适当的条件 ,使得
△EAB≌△BCD.【解析】∵∠A=∠C=90°,AB=CD,
∴若利用“SAS”,可添加AE=CB,
若利用“HL”,可添加EB=BD,
若利用“ASA”或“AAS”,可添加∠EBD=90°,
若添加∠E=∠DBC,可利用“AAS”证明.综上所述,可添加的条件为AE=CB(或EB=BD或∠EBD=90°或∠E=∠DBC等).
答案:AE=CB(或EB=BD或∠EBD=90°或∠E=∠DBC等,答案不唯一)【高手支招】在解决开放性探究问题时,首先从题中找到已知条件、隐含条件和可证出的条件,然后再利用三角形全等的判定条件来寻找缺少的条件.4.如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A,B两点作AC⊥l交l于点C,BD⊥l交l于点D.
求证:AC=OD.【证明】∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵AC⊥l,BD⊥l,
∴∠ACO=∠BDO=90°,
∴∠A+∠AOC=90°,
∴∠A=∠BOD,
在△AOC和△OBD中,
∠A=∠BOD,∠ACO=∠BDO=90°,OA=OB,
∴△AOC≌△OBD(AAS),∴AC=OD.5.在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF.
(2)若∠CAE=30°,∠BAC=45°,求∠ACF的度数.【解析】(1)∵∠ABC=90°,
∴△ABE和△CBF均为直角三角形,
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
(2)∵Rt△ABE≌Rt△CBF,∴∠BAE=∠BCF,
又∵∠CAE=30°,∠BAC=45°,
∴∠BAE=15°,∴∠BCF=15°,
又∠ABC=90°,AB=CB,∴∠ACB=45°,
∴∠ACF=45°+15°=60°.【想一想错在哪?】两个三角形的两边及其中一边上的高对应相等,这两个三角形是否全等?若全等,请给出证明;若不全等,请说明理由.提示:此题没考虑一个三角形是锐角三角形,而另一个三角形为钝角三角形的情况.
2.会选用合适的方法判定两个直角三角形全等.(难点)斜边、直角边定理
如图,在△ABC与△DEF中,∠A=∠D=90°,AB=DE,BC=EF.【思考】
(1)AC与DF相等吗?为什么?
提示:AC=DF.理由如下:
∵∠A=∠D=90°,
根据勾股定理得AB2+AC2=BC2,DE2+DF2=EF2,
又∵AB=DE,BC=EF,∴AC=DF.
(2)△ABC与△DEF全等吗?为什么?
提示:全等.∵AB=DE,BC=EF,AC=DF.
∴△ABC≌△DEF(SSS).【总结】
斜边、直角边定理:_____和一条_______对应相等的两个
直角三角形全等(可以简写成“_____________”或“___”).斜边直角边斜边、直角边HL (打“√”或“×”)
(1)“HL”定理适合所有三角形全等的判定. ( )
(2)判定两个直角三角形全等只能用“HL”定理. ( )
(3)有两条边对应相等的三角形全等. ( )
(4)一条直角边和一个锐角对应相等的三角形全等. ( )×××√知识点 1 应用“HL”证明直角三角形全等?
【例1】如图,在△ABC中,∠B=90°,AD为
∠BAC的平分线,DF⊥AC于F,DE=DC,那么
BE=CF吗?请说明理由.
【思路点拨】先下结论BE=CF,再说明理由:先证∠BAD=∠CAD,
∠B=∠AFD,得出△ABD≌△AFD,BD=FD,再证Rt△EBD≌Rt△CFD,
证得BE=CF.【自主解答】BE=CF.理由如下:
∵AD为∠BAC的平分线,∴∠BAD=∠CAD.
∵DF⊥AC,∴∠AFD=90°.
又∠B=90°,∴∠B=∠AFD.
在△ABD和△AFD中,
∴△ABD≌△AFD(AAS),∴BD=FD.在Rt△EBD和Rt△CFD中,
∴Rt△EBD≌Rt△CFD(HL),∴BE=CF.【总结提升】应用“HL”应注意的三个问题
1.“HL”是判定两个直角三角形全等的方法,对于一般的三角形不成立,在使用时一定要注意其应用的范围.
2.在书写格式上,三角形的前面必须注明“Rt”.
3.在题设中,没有指明但又是直角三角形的,必须依照定义说明或推证是直角三角形,否则不能直接应用“HL”.知识点 2 选定合适方法判定直角三角形全等?
【例2】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE.
(2)如图2,若BE
的延长线交AC于点F,且BF⊥AC,
垂足为F,∠BAC=45°,原题设其他条件不变.
求证:△AEF≌△BCF.【思路点拨】(1)根据等腰三角形三线合一的性质可得∠BDE=
∠CDE,然后利用“边角边”证明△BDE和△CDE全等即可.
(2)先判定△ABF为等腰直角三角形,再根据等腰直角三角形的
两直角边相等可得AF=BF,再根据同角的余角相等求出∠EAF=
∠CBF,然后利用“角边角”证明△AEF和△BCF全等即可.【自主解答】(1)∵AB=AC,D是BC的中点,
∴∠BDE=∠CDE=90°,
在△BDE和△CDE中,
∴△BDE≌△CDE(SAS),
∴BE=CE.(2)∵∠BAC=45°,BF⊥AF,
∴△ABF为等腰直角三角形,∴AF=BF,
∵AB=AC,点D是BC的中点,∴AD⊥BC,
∴∠EAF+∠C=90°,
∵BF⊥AC,∴∠CBF+∠C=90°,
∴∠EAF=∠CBF,
在△AEF和△BCF中,
∴△AEF≌△BCF(ASA).【总结提升】判定直角三角形全等的方法选择题组一:应用“HL”证明直角三角形全等
1.如图,四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为 ( )
A.145° B.130° C.110° D.70°【解析】选C.∵∠ABC=∠ADC=90°,
∴在Rt△ABC与Rt△ADC中,
CB=CD,AC=AC,
∴△ABC≌△ADC,又∠BAC=35°,
∴∠ACD=∠ACB=55°,
∴∠BCD=110°.2.如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是 ( )
A.∠DAE=∠CBE
B.CE=DE
C.△DAE与△CBE不一定全等
D.∠1=∠2【解析】选C.∵AD=BC,∠C=∠D=90°,∠DEA=∠CEB,
∴△DAE≌△CBE(C选项不正确),
∴∠DAE=∠CBE(A选项正确),
CE=DE(B选项正确),
∵AD=BC,∠C=∠D=90°,AB=BA,
∴△ABC≌△BAD.
∴∠1=∠2(D选项正确).3.如图,长方形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有 ( )
A.3对 B.4对 C.5对 D.6对
【解析】选B.图中全等的直角三角形有:△AED≌△FEC,
△BDC≌△FDC≌△DBA,共4对.【变式训练】如图,AC,BD是长方形ABCD的
对角线,过点D作DE∥AC交BC的延长线于E,
则图中与△ABC全等的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【解析】选D.与△ABC全等的三角形为△ADC,△BAD,△DCB,
△DCE共4个.4.如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为 ;若添加条件AC=EC,则可以用 判定全等.【解析】∵AB⊥BD,AB∥ED,∴ED⊥BD,
∴∠B=∠D=90°;
①又∵AB=ED,
∴在△ABC和△EDC中,当BC=DC时,△ABC≌△EDC(SAS);
②在Rt△ABC和Rt△EDC中,AB=ED,AC=EC,由“HL”定理可得Rt△ABC≌Rt△EDC(HL).
答案:BC=DC HL5.如图,△ABC中,∠ABC=45°,AD⊥BC于D,
点E在AD上,且BE=AC,求证:DE=CD.
【证明】∵∠ABC=45°,AD⊥BC,
∴AD=BD,∠BDE=∠ADC=90°.
又∵BE=AC,
∴△BDE≌△ADC(HL).
∴DE=CD.6.如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线,交AC于点E.求证:AE=ED.【证明】连接BE,∵DE为BC的垂线,∴∠BDE=90°.
∴∠BDE=∠A.
在Rt△BDE和Rt△BAE中,
∴Rt△BDE≌Rt△BAE(HL),∴AE=ED.题组二:选定合适方法判定直角三角形全等
1.如图,E是正方形ABCD的边DC上一点,过点A
作FA⊥AE交CB的延长线于点F.若AB=4,则四
边形AFCE的面积是 ( )
A.4 B.8 C.16 D.无法计算【解析】选C.∵∠EAD+∠BAE=90°,
∠FAB+∠BAE=90°,∴∠FAB=∠EAD.
∵四边形ABCD为正方形,
∴AB=AD,∠D=∠ABF=90°.
在△ABF和△ADE中,
∴△ABF≌△ADE(ASA),
∴四边形AFCE的面积与正方形ABCD的面积相等,
∴S四边形AFCE=S正方形ABCD=AB2=16.2.把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
(1) ,∠A=∠D(ASA).
(2)AC=DF, (SAS).
(3)AB=DE,BC=EF( ).
(4)AC=DF, (HL).
(5)∠A=∠D,BC=EF( ).
(6) ,AC=DF(AAS).【解析】要利用题中的“直角三角形有一个角是直角”的条件,找准对应元素及三角形全等的判定方法.
答案:(1)AC=DF (2)CB=FE (3)HL
(4)AB=DE (5)AAS (6)∠B=∠E3.如图,A,B,C三点在同
一条直线上,∠A=∠C=90°,AB=CD,请添加
一个适当的条件 ,使得
△EAB≌△BCD.【解析】∵∠A=∠C=90°,AB=CD,
∴若利用“SAS”,可添加AE=CB,
若利用“HL”,可添加EB=BD,
若利用“ASA”或“AAS”,可添加∠EBD=90°,
若添加∠E=∠DBC,可利用“AAS”证明.综上所述,可添加的条件为AE=CB(或EB=BD或∠EBD=90°或∠E=∠DBC等).
答案:AE=CB(或EB=BD或∠EBD=90°或∠E=∠DBC等,答案不唯一)【高手支招】在解决开放性探究问题时,首先从题中找到已知条件、隐含条件和可证出的条件,然后再利用三角形全等的判定条件来寻找缺少的条件.4.如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A,B两点作AC⊥l交l于点C,BD⊥l交l于点D.
求证:AC=OD.【证明】∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵AC⊥l,BD⊥l,
∴∠ACO=∠BDO=90°,
∴∠A+∠AOC=90°,
∴∠A=∠BOD,
在△AOC和△OBD中,
∠A=∠BOD,∠ACO=∠BDO=90°,OA=OB,
∴△AOC≌△OBD(AAS),∴AC=OD.5.在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF.
(2)若∠CAE=30°,∠BAC=45°,求∠ACF的度数.【解析】(1)∵∠ABC=90°,
∴△ABE和△CBF均为直角三角形,
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
(2)∵Rt△ABE≌Rt△CBF,∴∠BAE=∠BCF,
又∵∠CAE=30°,∠BAC=45°,
∴∠BAE=15°,∴∠BCF=15°,
又∠ABC=90°,AB=CB,∴∠ACB=45°,
∴∠ACF=45°+15°=60°.【想一想错在哪?】两个三角形的两边及其中一边上的高对应相等,这两个三角形是否全等?若全等,请给出证明;若不全等,请说明理由.提示:此题没考虑一个三角形是锐角三角形,而另一个三角形为钝角三角形的情况.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
