2020湘教版八下数学1.4角平分线的性质习题课件(33张PPT)
文档属性
| 名称 | 2020湘教版八下数学1.4角平分线的性质习题课件(33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 700.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览










文档简介
课件33张PPT。1.4 角平分线的性质?1.掌握角平分线的性质定理和判定定理.(重点)
2.能够运用角平分线的性质定理和判定定理解决几何问题.(重点、难点)一、角平分线的性质与判定
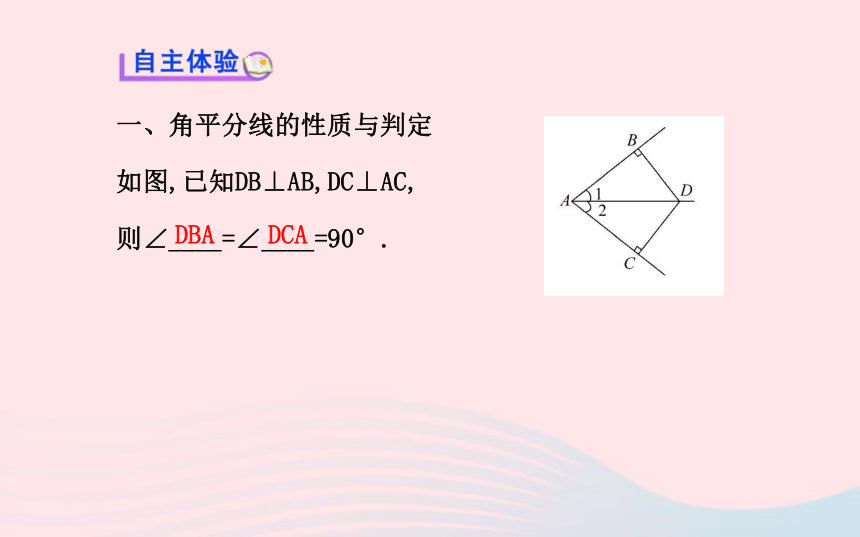
如图,已知DB⊥AB,DC⊥AC,
则∠____=∠____=90°.DBADCA【思考】
(1)如果∠1=∠2,那么BD=CD吗?为什么?
提示:BD=CD.∵DB⊥AB,DC⊥AC,∠DBA=∠DCA=90°,又∵∠1=∠2,AD=AD,
∴△ABD≌△ACD(AAS),∴BD=CD.
(2)如果BD=CD,那么∠1=∠2吗?为什么?
提示:∠1=∠2.∵BD=CD,AD=AD,∴Rt△ABD≌Rt△ACD(HL),
∴∠1=∠2.【总结】(1)角平分线的性质定理:角的平分线上的点到角的两
边的距离_____.
(2)角平分线的判定定理:角的内部到角的两边距离_____的点
在角的平分线上.相等相等二、三角形三条角平分线的性质
到三角形三条边的距离相等的点是其任意两角的_______的交
点,此点也在另一个角的_______上.平分线平分线 (打“√”或“×”)
(1)角的平分线就是角的对称轴. ( )
(2)到角的两边距离相等的点有无数个. ( )
(3)到角的两边距离相等的点,在这个角的平分线上. ( )
(4)三角形三条角平分线的交点可能在三角形的外部. ( )
(5)三角形三条角平分线的交点到三角形三个顶点的距离相等.
( )×√×××知识点 1 角平分线的性质?
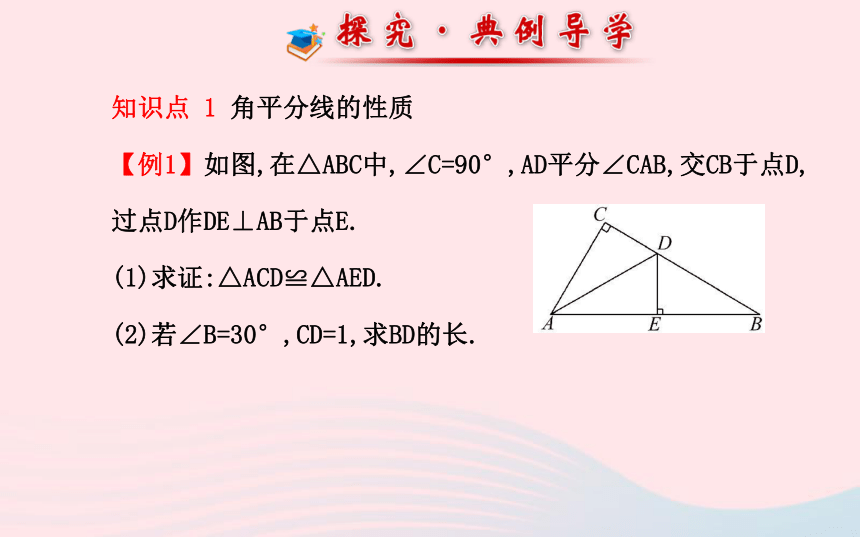
【例1】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED.
(2)若∠B=30°,CD=1,求BD的长.【解题探究】(1)①CD与ED有什么关系?为什么?
提示:CD=ED.∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=ED.
②由CD与ED的关系能判定△ACD≌△AED吗?为什么?
提示:能.∵在Rt△ACD和Rt△AED中,AD=AD,CD=ED,∴由“HL”定理可得Rt△ACD≌Rt△AED.(2)①BD与ED有什么关系?为什么?
提示:BD=2ED.∵DE⊥AB,∴∠DEB=90°,
又∵∠B=30°,∴BD=2ED.
②请结合CD的长,以及CD与ED的关系确定BD的长.
提示:∵ED=CD=1,∴BD=2ED=2.【总结提升】角平分线图形结构中的两种数量关系
如图,OC平分∠AOB,PD⊥OA,PE⊥OB,DE交OC于点F,
可以得到以下结论:
1.角之间的相等关系:
∠AOC=∠BOC=∠PDF=∠PEF;
∠ODP=∠OEP=∠DFO=∠EFO=∠DFP=∠EFP;∠DPO=∠EPO=∠ODF=∠OEF.
2.线段的相等关系:
OD=OE,DP=EP,DF=EF.知识点 2 角平分线的判定?
【例2】如图,在四边形ABCD中,∠ADC+
∠ABC=180°,BC=DC,CE⊥AD交AD的延长
线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
【思路点拨】
证∠ABC=∠CDE,∠CFB=∠CED→△CFB≌△CED→CF=CE→结论【自主解答】∵∠ADC+∠ABC=180°,
又∵∠ADC+∠CDE=180°,∴∠ABC=∠CDE.
∵CF⊥AB,CE⊥AD,
∴∠CFB=∠CED=90°.
在Rt△CFB和Rt△CED中,
∴△CFB≌△CED(AAS),
∴CF=CE,
∴AC平分∠BAD.【总结提升】证明角平分线的两种方法
1.定义法:应用角平分线的定义.
2.定理法:应用“到角两边距离相等的点在角的平分线上”来判定.判定角平分线时,需要满足两个条件:“垂直”和“相等”.若已知“垂直”,则设法证“相等”;若已知“相等”,则设法证“垂直”.题组一:角平分线的性质
1.在△ABC中,∠BAC=90°,
AB=3,AC=4.AD平分∠BAC交BC于D,则BD的
长为( )【解析】选A.∵∠BAC=90°,AB=3,AC=4,
∴BC=
∴BC边上的高=3×4÷5=
∵AD平分∠BAC,
∴点D到AB,AC上的距离相等,设为h,
则
解得
S△ABD=
解得2.如图,BD是∠ABC的
平分线,P是BD上的一点,PE⊥BA于点E,
PE=4cm,则点P到边BC的距离为 cm.
【解析】过点P作PF⊥BC于点F,根据“角平分线上的点到角的两边距离相等”知PF=PE=4cm,即点P到边BC的距离为4cm.
答案:43.如图,在△ABC中,∠ACB=90°,AD是△ABC的
角平分线,BC=10cm,BD∶DC=3∶2,则点D到AB
的距离为 cm.
【解析】∵BC=10cm,BD∶DC=3∶2,∴DC=4cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC,即点D到AB的距离等于4cm.
答案:44.如图,Rt△ABC中,
∠C=90°,AD平分∠CAB,DE⊥AB于E,若
AC=6,BC=8,CD=3.
(1)求DE的长.
(2)求△ADB的面积.【解析】(1)在Rt△ABC中,∠C=90°,∴AC⊥CD.又AD平分
∠CAB,DE⊥AB,∴DE=CD,又CD=3,∴DE=3.
(2)在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB=
∴S△ADB=题组二:角平分线的判定
1.如图所示,OB与OC分别是△ABC的∠ABC和∠ACB的平分线,那么∠BAO与∠CAO的大小关系为 ( )
A.∠BAO>∠CAO B.∠BAO=∠CAO
C.∠BAO<∠CAO D.不确定【解析】选B.∵OB与OC分别是△ABC的∠ABC和∠ACB的平分线,∴点O到AB,BC,AC的距离相等,
∴点O也在∠BAC的平分线上,∴∠BAO=∠CAO.2.如图所示,DE⊥AB于D,CE⊥BC于C,且DE=CE,则下列结论不一定正确的是 ( )
A.BE平分∠ABC
B.BE平分∠CED
C.AE+DE=AC
D.∠A=∠ABE【解析】选D.由DE⊥AB,CE⊥BC,DE=CE可判断BE平分∠ABC;由条件可证得△BCE≌△BDE,所以∠BEC=∠BED,所以BE平分∠CED.
∵AC=AE+CE,而CE=DE,
∴AC=AE+DE.∵D不一定为AB中点,故△EDB和△EDA不一定全等,故得不到∠A=∠ABE.3.如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物
中转站,要求它到三条公路的距离相等,则可供选择的地址有
( )
A.一处 B.两处 C.三处 D.四处【解析】选D.因为到角的两边的距离相等的点在角的平分线上,所以可供选择的地点可在这三条直线围成的三角形的内角平分线的交点处或这个三角形的外角平分线的交点处.如图,可供选择的地址有P1,P2,P3,P4共四处.【高手支招】有关到线段距离相等的点的位置确定,一般是利用“到角两边距离相等的点在角的平分线上”这一定理,作出由线段所组成的角的角平分线,确定点的位置.4.如图,∠AOB =70°,
QC⊥OA于C,QD⊥OB于D,若QC = QD,则
∠AOQ= °.
【解析】∵QC⊥OA,QD⊥OB,QC = QD,∴点Q在∠AOB的平分线
上,∴∠AOQ= ∠AOB,
∵∠AOB=70°,∴∠AOQ =35°.
答案:355.已知:如图,AB=CD,△PAB的面积与△PCD的面积相等,求证:OP平分∠AOD.【证明】过点P作PE⊥OA于E,PF⊥OD于F,
∵S△PAB=S△PCD,
∴ AB·PE= CD·PF.
∵AB=CD,∴PE=PF.
∴点P在∠AOD的平分线上(到一个角的两边距离相等的点在这个角的平分线上).
∴OP平分∠AOD.6.如图,△ABC中,BP,CP分别是∠B,∠C的外角平分线.
求证:点P在∠A的平分线上.【证明】过点P作PM⊥AB,PN⊥AC,PQ⊥BC,垂足分别为M,N,Q.
∵点P在∠B的外角∠CBM的平分线上,∴PM=PQ.
∵点P在∠C的外角∠BCN的平分线上,
∴PN=PQ,∴PM=PN,而PM⊥AB,PN⊥AC,
∴点P在∠A的平分线上.【想一想错在哪?】如图,AD平分∠EAF,BC过点D垂直于AD,分别交AE,AF于B,C.求证:BD=DC.
提示:这里错在没有正确理解角的平分线的性质,应是“角的平分线上的点到两边的距离”,这里的BD,CD不是到两边的距离.
2.能够运用角平分线的性质定理和判定定理解决几何问题.(重点、难点)一、角平分线的性质与判定
如图,已知DB⊥AB,DC⊥AC,
则∠____=∠____=90°.DBADCA【思考】
(1)如果∠1=∠2,那么BD=CD吗?为什么?
提示:BD=CD.∵DB⊥AB,DC⊥AC,∠DBA=∠DCA=90°,又∵∠1=∠2,AD=AD,
∴△ABD≌△ACD(AAS),∴BD=CD.
(2)如果BD=CD,那么∠1=∠2吗?为什么?
提示:∠1=∠2.∵BD=CD,AD=AD,∴Rt△ABD≌Rt△ACD(HL),
∴∠1=∠2.【总结】(1)角平分线的性质定理:角的平分线上的点到角的两
边的距离_____.
(2)角平分线的判定定理:角的内部到角的两边距离_____的点
在角的平分线上.相等相等二、三角形三条角平分线的性质
到三角形三条边的距离相等的点是其任意两角的_______的交
点,此点也在另一个角的_______上.平分线平分线 (打“√”或“×”)
(1)角的平分线就是角的对称轴. ( )
(2)到角的两边距离相等的点有无数个. ( )
(3)到角的两边距离相等的点,在这个角的平分线上. ( )
(4)三角形三条角平分线的交点可能在三角形的外部. ( )
(5)三角形三条角平分线的交点到三角形三个顶点的距离相等.
( )×√×××知识点 1 角平分线的性质?
【例1】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED.
(2)若∠B=30°,CD=1,求BD的长.【解题探究】(1)①CD与ED有什么关系?为什么?
提示:CD=ED.∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=ED.
②由CD与ED的关系能判定△ACD≌△AED吗?为什么?
提示:能.∵在Rt△ACD和Rt△AED中,AD=AD,CD=ED,∴由“HL”定理可得Rt△ACD≌Rt△AED.(2)①BD与ED有什么关系?为什么?
提示:BD=2ED.∵DE⊥AB,∴∠DEB=90°,
又∵∠B=30°,∴BD=2ED.
②请结合CD的长,以及CD与ED的关系确定BD的长.
提示:∵ED=CD=1,∴BD=2ED=2.【总结提升】角平分线图形结构中的两种数量关系
如图,OC平分∠AOB,PD⊥OA,PE⊥OB,DE交OC于点F,
可以得到以下结论:
1.角之间的相等关系:
∠AOC=∠BOC=∠PDF=∠PEF;
∠ODP=∠OEP=∠DFO=∠EFO=∠DFP=∠EFP;∠DPO=∠EPO=∠ODF=∠OEF.
2.线段的相等关系:
OD=OE,DP=EP,DF=EF.知识点 2 角平分线的判定?
【例2】如图,在四边形ABCD中,∠ADC+
∠ABC=180°,BC=DC,CE⊥AD交AD的延长
线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
【思路点拨】
证∠ABC=∠CDE,∠CFB=∠CED→△CFB≌△CED→CF=CE→结论【自主解答】∵∠ADC+∠ABC=180°,
又∵∠ADC+∠CDE=180°,∴∠ABC=∠CDE.
∵CF⊥AB,CE⊥AD,
∴∠CFB=∠CED=90°.
在Rt△CFB和Rt△CED中,
∴△CFB≌△CED(AAS),
∴CF=CE,
∴AC平分∠BAD.【总结提升】证明角平分线的两种方法
1.定义法:应用角平分线的定义.
2.定理法:应用“到角两边距离相等的点在角的平分线上”来判定.判定角平分线时,需要满足两个条件:“垂直”和“相等”.若已知“垂直”,则设法证“相等”;若已知“相等”,则设法证“垂直”.题组一:角平分线的性质
1.在△ABC中,∠BAC=90°,
AB=3,AC=4.AD平分∠BAC交BC于D,则BD的
长为( )【解析】选A.∵∠BAC=90°,AB=3,AC=4,
∴BC=
∴BC边上的高=3×4÷5=
∵AD平分∠BAC,
∴点D到AB,AC上的距离相等,设为h,
则
解得
S△ABD=
解得2.如图,BD是∠ABC的
平分线,P是BD上的一点,PE⊥BA于点E,
PE=4cm,则点P到边BC的距离为 cm.
【解析】过点P作PF⊥BC于点F,根据“角平分线上的点到角的两边距离相等”知PF=PE=4cm,即点P到边BC的距离为4cm.
答案:43.如图,在△ABC中,∠ACB=90°,AD是△ABC的
角平分线,BC=10cm,BD∶DC=3∶2,则点D到AB
的距离为 cm.
【解析】∵BC=10cm,BD∶DC=3∶2,∴DC=4cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC,即点D到AB的距离等于4cm.
答案:44.如图,Rt△ABC中,
∠C=90°,AD平分∠CAB,DE⊥AB于E,若
AC=6,BC=8,CD=3.
(1)求DE的长.
(2)求△ADB的面积.【解析】(1)在Rt△ABC中,∠C=90°,∴AC⊥CD.又AD平分
∠CAB,DE⊥AB,∴DE=CD,又CD=3,∴DE=3.
(2)在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB=
∴S△ADB=题组二:角平分线的判定
1.如图所示,OB与OC分别是△ABC的∠ABC和∠ACB的平分线,那么∠BAO与∠CAO的大小关系为 ( )
A.∠BAO>∠CAO B.∠BAO=∠CAO
C.∠BAO<∠CAO D.不确定【解析】选B.∵OB与OC分别是△ABC的∠ABC和∠ACB的平分线,∴点O到AB,BC,AC的距离相等,
∴点O也在∠BAC的平分线上,∴∠BAO=∠CAO.2.如图所示,DE⊥AB于D,CE⊥BC于C,且DE=CE,则下列结论不一定正确的是 ( )
A.BE平分∠ABC
B.BE平分∠CED
C.AE+DE=AC
D.∠A=∠ABE【解析】选D.由DE⊥AB,CE⊥BC,DE=CE可判断BE平分∠ABC;由条件可证得△BCE≌△BDE,所以∠BEC=∠BED,所以BE平分∠CED.
∵AC=AE+CE,而CE=DE,
∴AC=AE+DE.∵D不一定为AB中点,故△EDB和△EDA不一定全等,故得不到∠A=∠ABE.3.如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物
中转站,要求它到三条公路的距离相等,则可供选择的地址有
( )
A.一处 B.两处 C.三处 D.四处【解析】选D.因为到角的两边的距离相等的点在角的平分线上,所以可供选择的地点可在这三条直线围成的三角形的内角平分线的交点处或这个三角形的外角平分线的交点处.如图,可供选择的地址有P1,P2,P3,P4共四处.【高手支招】有关到线段距离相等的点的位置确定,一般是利用“到角两边距离相等的点在角的平分线上”这一定理,作出由线段所组成的角的角平分线,确定点的位置.4.如图,∠AOB =70°,
QC⊥OA于C,QD⊥OB于D,若QC = QD,则
∠AOQ= °.
【解析】∵QC⊥OA,QD⊥OB,QC = QD,∴点Q在∠AOB的平分线
上,∴∠AOQ= ∠AOB,
∵∠AOB=70°,∴∠AOQ =35°.
答案:355.已知:如图,AB=CD,△PAB的面积与△PCD的面积相等,求证:OP平分∠AOD.【证明】过点P作PE⊥OA于E,PF⊥OD于F,
∵S△PAB=S△PCD,
∴ AB·PE= CD·PF.
∵AB=CD,∴PE=PF.
∴点P在∠AOD的平分线上(到一个角的两边距离相等的点在这个角的平分线上).
∴OP平分∠AOD.6.如图,△ABC中,BP,CP分别是∠B,∠C的外角平分线.
求证:点P在∠A的平分线上.【证明】过点P作PM⊥AB,PN⊥AC,PQ⊥BC,垂足分别为M,N,Q.
∵点P在∠B的外角∠CBM的平分线上,∴PM=PQ.
∵点P在∠C的外角∠BCN的平分线上,
∴PN=PQ,∴PM=PN,而PM⊥AB,PN⊥AC,
∴点P在∠A的平分线上.【想一想错在哪?】如图,AD平分∠EAF,BC过点D垂直于AD,分别交AE,AF于B,C.求证:BD=DC.
提示:这里错在没有正确理解角的平分线的性质,应是“角的平分线上的点到两边的距离”,这里的BD,CD不是到两边的距离.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
